灰度共生矩阵的应用及特点

在图像中任取一点（x，y）以及偏离它的另一点（x+a，y+b），形成一个点对，设该点对的灰度值为（i，j），即点（x，y）的灰度为i，点（x+a，y+b）的灰度为j。固定点a与点b，令点（x，y）在整幅图像上移动，则会得到各种（i，j）的值。设灰度值的级数为L，则i与j的组合共有L²种。在整幅图像中，统计出每一种（i，j）值出现的次数，再将它们归一化为出现的概率P_ij，则称方阵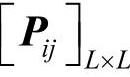为灰度联合概率矩阵，也称为灰度共生矩阵。灰度共生矩阵实际上就是两像素点的联合直方图，其形成过程如图3-15所示。

距离差分值（a，b）取不同的数值组合，可以得到沿一定方向（如0°、45°、90°、135°）相隔一定距离的像元之间灰度联合概率矩阵。a和b的取值要根据纹理周期分布的特性来选择。当a与b取值较小时，对应于变化缓慢的纹理图像（粗纹理），其灰度联合概率矩阵对角线上的数值较大，倾向于作对角线分布；若纹理的变化较快，则对角线上的数值越小，而对角线两侧上的元素值增大，倾向于均匀分布。

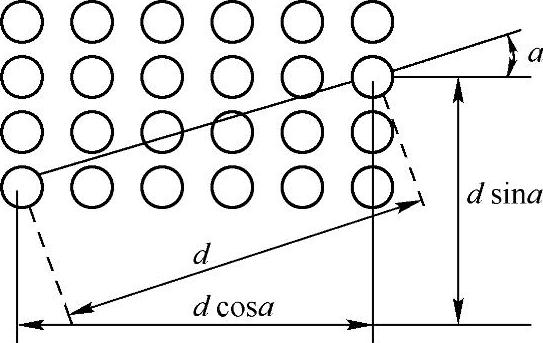
图3-15 灰度共生矩阵的形成过程

为了能更直观地以共生矩阵描述纹理状况，研究者从灰度共生矩阵导出一些反映矩阵状况的参数，典型的有以下几种。

（1）能量

灰度共生矩阵元素值的平方和，也称能量。它反映了图像灰度分布的均匀程度和纹理粗细度。能量的数学定义式如下。

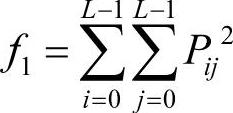
当P_ij数值分布较集中时，能量较大；当P_ij数值分布较分散时，则能量较小。

（2）相关

相关是度量空间灰度共生矩阵元素在行或列方向上的相似程度，因此，相关值大小反映了图像中局部灰度相关性。当矩阵元素值均匀相等时，相关值就大；相反，如果矩阵像元值相差很大，则相关值就小。相关的数学定义式如下。

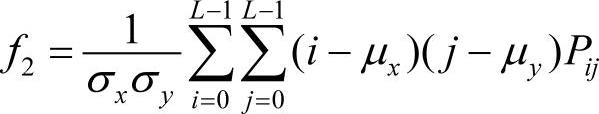(www.xing528.com)

式中，μ_x、µ_y、σ_x、σ_y分别为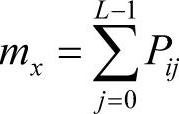与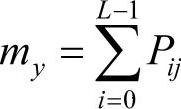的均值和标准差。

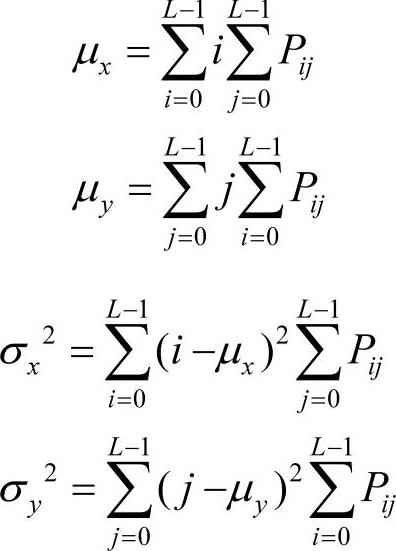
（3）熵

熵是图像所具有的信息量的度量，纹理信息也属于图像的信息，是一个随机性的度量，它表示了图像中纹理的非均匀程度或复杂程度。熵的数学表达式如下。

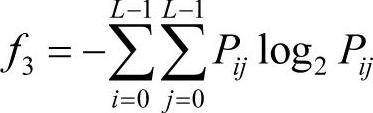
若P_ij分布比较均匀时，则熵较大；反之，P_ij数值分布比较集中时，则熵较小。

（4）反差

反差又称主对角线的惯性矩，其数学表达式如下。

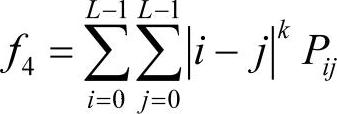
对于粗纹理，P_ij的数值集中于主对角线附近，此时|i-j|的值较小，所以反差也较小；反之，对于细纹理，P_ij的数值比较均匀，因此，反差较大。