熟练掌握数学形态学的基本运算

用形态学的方法处理和分析图像即是对物体或目标的形态分析，本小节主要介绍二值形态分析方法中最基本的几种运算，即腐蚀、膨胀以及由它们组合得到的开闭运算和边界检测算法。

首先来定义一些基本运算和符号。

➢元素：设有一幅图像X，若点a在X的区域以内，则称a为X的元素，记作a∈X，如图2-60所示。

➢B包含于X：设有两幅图像B，X。对于B中所有的元素ai，都有ai∈X，则称B包含于X，记作BX，如图2-61所示。

图2-60 元素

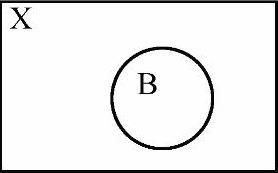
图2-61 包含

➢B击中X：设有两幅图像B，X。若存在这样一个点，它既是B的元素，又是X的元素，则称B击中X，记作B↑X，如图2-62所示。

➢B不击中X：设有两幅图像B，X。若不存在任何一个点，它既是B的元素，又是X的元素，即B和X的交集是空，则称B不击中X，记作B∩X=Φ；其中∩是集合运算相交的符号，Φ表示空集，如图2-63所示。

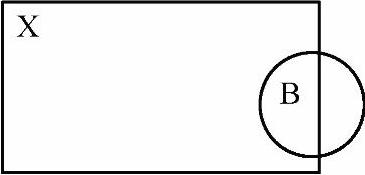
图2-62 击中

图2-63 不击中

➢补集：设有一幅图像X，所有X区域以外的点构成的集合称为X的补集，记作X^c，如图2-64所示。在图2-63中，显然，如果B∩X=Φ，则B在X的补集内，即BX^c。

➢结构元素：设有两幅图像B、X。若X是被处理的对象，而B是用来处理X的，则称B为结构元素，又被形象地称作刷子。结构元素通常都是一些比较小的图像。

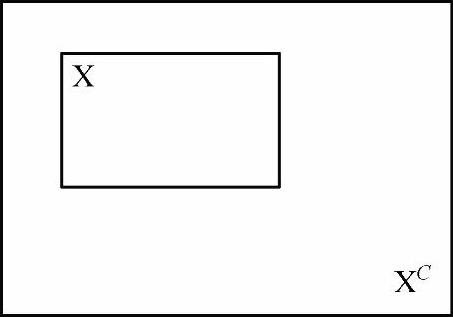
图2-64 补集的示意图

➢对称集：设有一幅图像B，将B中所有元素的坐标取反，即令（x，y）变成（-x，-y），所有这些点构成的新的集合称为B的对称集，记作B^v，如图2-65所示。

➢平移：设有一幅图像B，有一个点a（x₀，y₀），将B平移a后的结果是把B中所有元素的横坐标加x₀，纵坐标加y₀，即令（x，y）变成（x+x₀，y+y₀），所有这些点构成的新的集合称为B的平移，记作B_a，如图2-66所示。

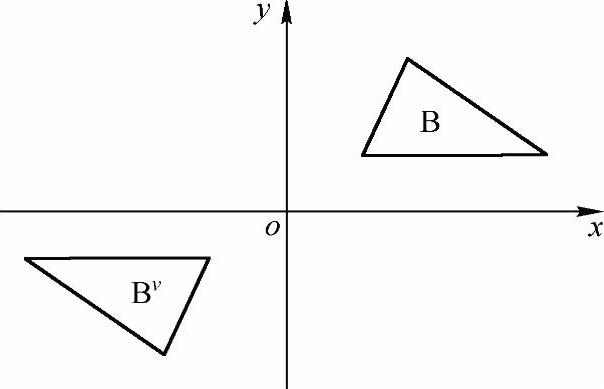
图2-65 对称集的示意图

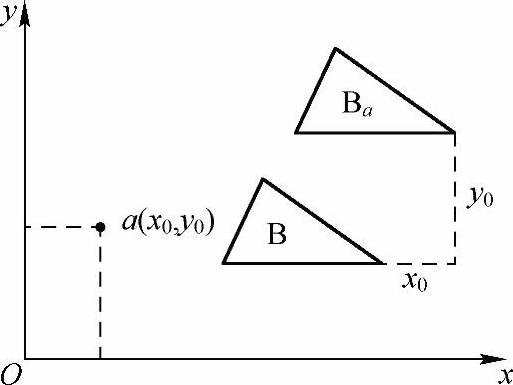
图2-66 平移的示意图

以上介绍了这么多基本符号和关系，现在来应用这些符号和关系，看一下形态学的基本运算。

（1）腐蚀

把结构元素B平移a后得到B_a，若B_a包含于X，我们记下这个a点，所有满足上述条件的a点组成的集合称作X被B腐蚀的结果。用公式表示为E（X）={a|B_aX}=XB，如图2-67所示。

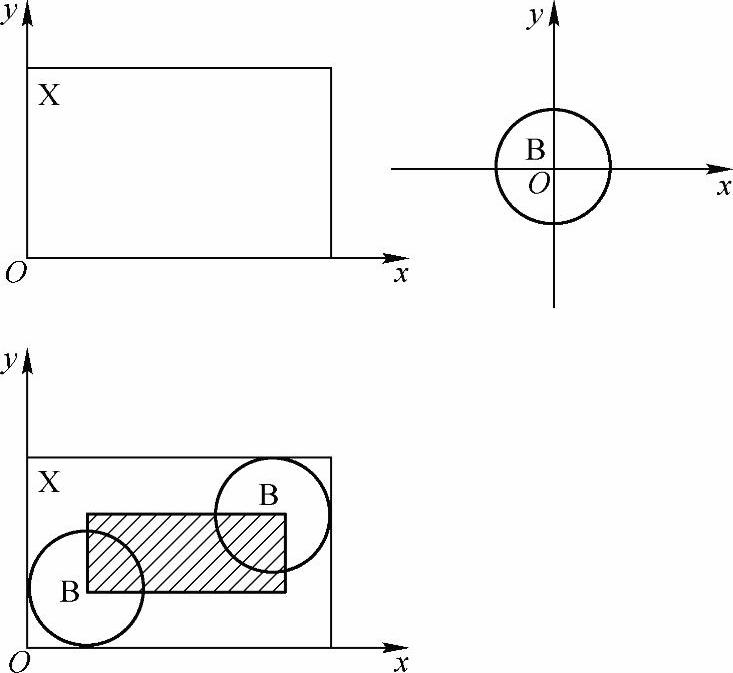
图2-67 腐蚀的示意图

图2-67中X是被处理的对象，B是结构元素。不难知道，对于任意一个在阴影部分的点a，B_a包含于X，所以X被B腐蚀的结果就是那个阴影部分。阴影部分在X的范围之内，且比X小，就像X被剥掉了一层，这就是叫腐蚀的原因。

在图2-68中，左边是被处理的图像X（二值图像，此处针对的是黑点），中间是结构元素B，那个标有origin的点是中心点，即当前处理元素的位置，在介绍模板操作时也有过类似的概念。腐蚀的方法是，拿B的中心点和X上的点一个一个地进行对比，如果B上的所有点都在X的范围内，则该点保留，否则将该点去掉；右边是腐蚀后的结果。可以看出，它仍在原来X的范围内，且比X包含的点要少，就像X被腐蚀掉了一层。

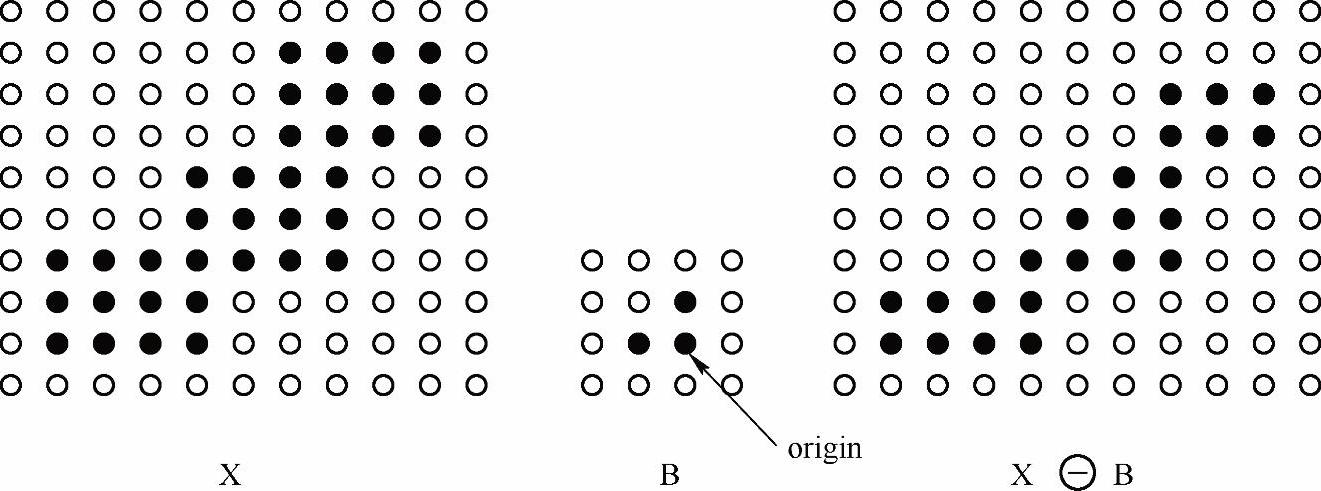
图2-68 腐蚀的示意图

如用0代表背景，1代表目标，设数字图像S和结构元素E为(www.xing528.com)

三角形“△”代表坐标原点，则用E对S腐蚀的结果为

（2）膨胀

膨胀可以看做是腐蚀的对偶运算，其定义是：把结构元素B平移a后得到B_a，若B_a击中X，我们记下这个a点。所有满足上述条件的a点组成的集合称作X被B膨胀的结果。用公式表示为：D（X）={a|B_a↑X}=XB，如图2-69所示。图2-69中X是被处理的对象，B是结构元素，不难知道，对于任意一个在阴影部分的点a，B_a击中X，所以X被B膨胀的结果就是那个阴影部分。阴影部分包括X的所有范围，就像X膨胀了一圈，这就是叫膨胀的原因。

现在来看看实际上是怎样进行膨胀运算的。在图2-70中，左边是被处理的图像X（二值图像，此处针对的是黑点），中间是结构元素B。膨胀的方法是，拿B的中心点和X上的点及X周围的点一个一个地进行比对，如果B上有一个点落在X的范围内，则该点就为黑；右边是膨胀后的结果。可以看出，它包括X的所有范围，就像X膨胀了一圈。

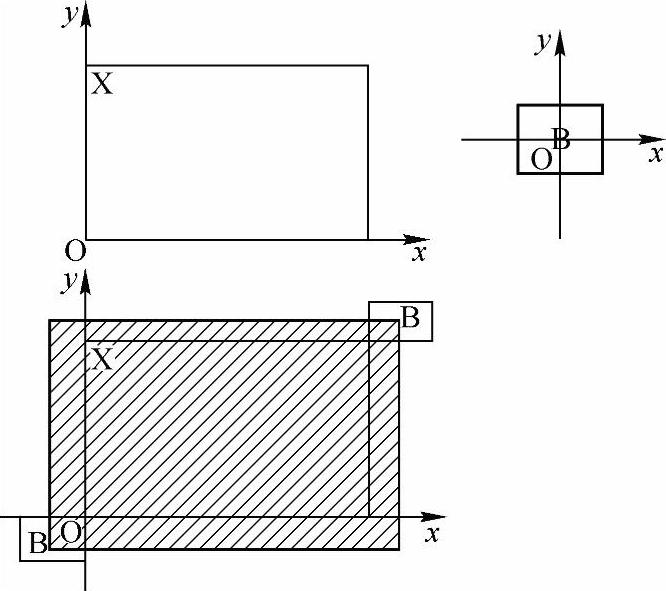
图2-69 膨胀的示意图

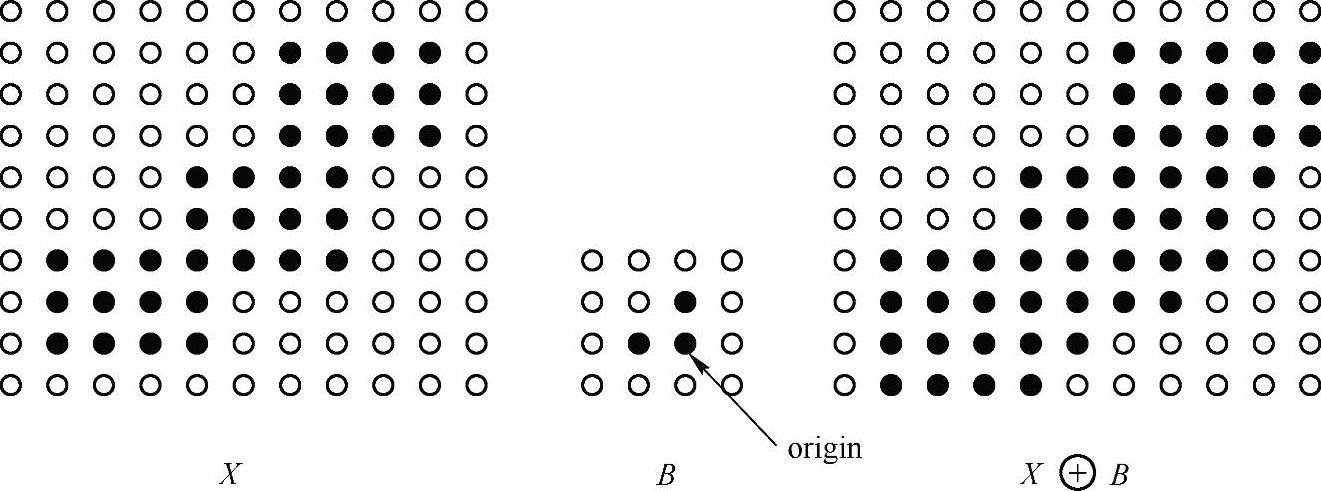
图2-70 膨胀运算

腐蚀运算和膨胀运算互为对偶的，用公式表示为（XB）^c=（X^c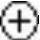B），即X被B腐蚀后的补集等于X的补集被B膨胀。这句话可以形象地理解为：河岸的补集为河面，河岸的腐蚀等价于河面的膨胀。读者可以自己举个例子来验证一下这个关系。在有些情况下，这个对偶关系是非常有用的。例如，某个图像处理系统用硬件实现了腐蚀运算，那么不必再另搞一套膨胀的硬件，直接利用该对偶就可以实现了。

例程2-44说明了如何对硬币图像进行腐蚀和膨胀操作，程序代码如下。其运行效果如图2-71所示。

例程2-44

图2-71 例程2-44运行效果

（3）开运算

先腐蚀后膨胀称为开，即OPEN（X）=D（E（X））。

现在来看一个开运算的例子（见图2-72）。在图2-72上面的两幅图中，左边是被处理的图像X（二值图像，此处针对的是黑点），右边是结构元素B，下面的两幅图中左边是腐蚀后的结果；右边是在此基础上膨胀的结果。可以看到，原图经过开运算后，一些孤立的小点被去掉了。一般来说，开运算能够去除孤立的小点、毛刺和小桥（即连通两块区域的小点），而总的位置和形状不变，这就是开运算的作用。

图2-72 开运算

（4）闭运算

先膨胀后腐蚀称为闭，即CLOSE（X）=E（D（X））。现在来看一个闭运算的例子（见图2-73）：

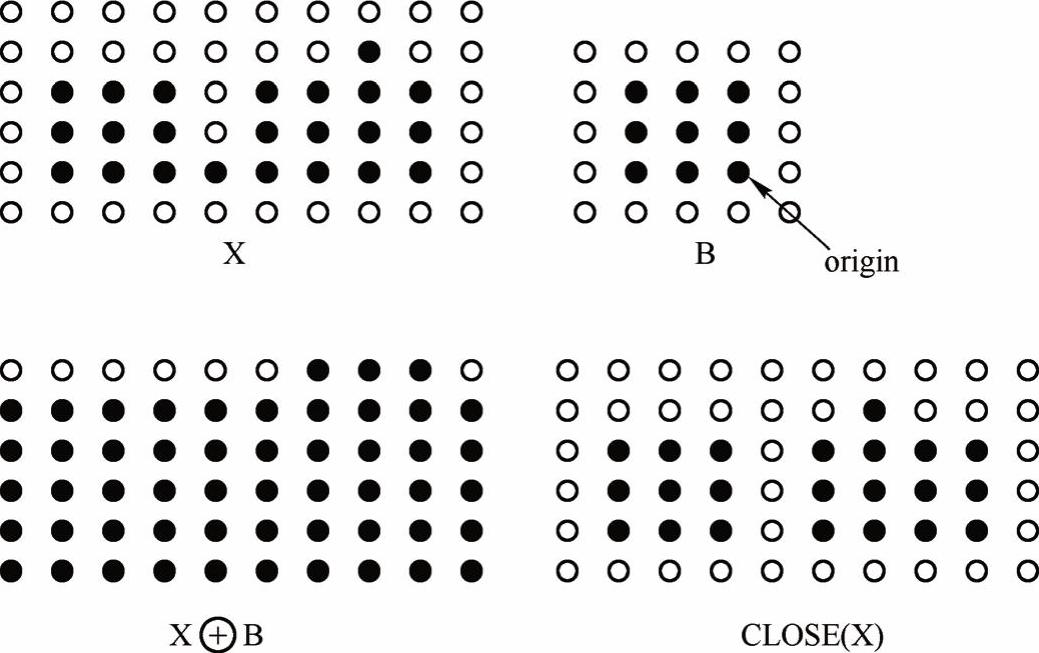
图2-73 闭运算

在图2-73上面的两幅图中，左边是被处理的图像X（二值图像，此处针对的是黑点），右边是结构元素B，下面的两幅图中左边是膨胀后的结果，右边是在此基础上腐蚀的结果。可以看到，原图经过闭运算后，断裂的地方被弥合了。一般来说，闭运算能够填平小孔，弥合小裂缝，而总的位置和形状不变。这就是闭运算的作用。

开和闭也是对偶运算。用公式表示为（OPEN（X））c=CLOSE（（X_c）），或者（CLOSE（X））c=OPEN（（X_c））。即X开运算的补集等于X的补集的闭运算，或者X闭运算的补集等于X的补集的开运算。这句话可以这样来理解：在两个小岛之间有一座小桥，可以把岛和桥看做是处理对象X，则X的补集为大海。如果涨潮时将小桥和岛的外围淹没（相当于用尺寸比桥宽大的结构元素对X进行开运算），那么两个岛的分隔，相当于小桥两边海域的连通（对X_c做闭运算）。

例程2-45是利用MATLAB实现二值图像开运算和闭运算的程序代码，其运行结果如图2-74所示。

例程2-45

图2-74 例程2-45运行结果