K-L变换的基本原理

设x=[x₁x₂…x_N]^T是一个N维随机矢量，其各分量的二阶矩存在，进一步假设得到了M个矢量采样x₁，x₂，…，x_M。在实际应用中，可将图像看成随机矢量。

例如，具有N个像素的图像f（m，n）在某个通信信道传输了N次，由于受到随机干扰，接收到的是一个图像样本集合{f₁（m，n），f₂（m，n），…，f_M（m，n）}。对第i次获得的图像f_i（m，n），可用一个N维随机列矢量x_i表示，从而图像样本集合可表示为{x₁，x₂，…，x_M}。

再例如，遥感多光谱图像的原始数据可用矩阵形式表示为

式中，N表示波段数，M表示每幅图像中像元的个数；矩阵X中每一行表示一个波段的图像。矩阵X中第i个列矢量可看成N伪随机列矢量的样本，记为x_i，从而矩阵X可表示为[x₁x₂…x_M]。

对于N维随机列矢量x=[x₁x₂…x_N]^T，其均值矢量与协方差矩阵可定义为

式中，C_x是N×N的实对称矩阵，其对角线元素c_ii为x_i的方差，c_ij为x_i与x_j之间的协方差，并且c_ij=c_ji。进一步，可以证明C_x是半正定的，即对于任意的N维列矢量y=[y₁y₂…y_N]^T，有y^TC_xy≥0。

在实际应用中，m_x与C_x可通过样本x₁，x₂，…，x_M来估计，即

由于C_x是半正定的，根据线性代数的知识可知，存在正交矩阵U=[u₁u₂…u_N]，使得C_x对角化，即

式中，I为单位矩阵；λ₁，λ₂，…，λ_N为C_x的特征根，且λ₁≥λ₂≥…≥λ_N≥0；u_i为C_x的与λ_i对应的归一化特征矢量，即

（λ_iI-C_x）u_i=0

随机列矢量x=[x₁x₂…x_N]^T的K-L变换定义为

y=U^T（x-m_x） （2-31）

其反变换为

x=Uy+m_x （2-32）(www.xing528.com)

对于遥感多光谱图像，K-L变换略有不同，即

y=U^Tx （2-33）

其反变换为

x=Uy （2-34）

遥感多光谱图像的K-L变换结果也可用矩阵形式表示，即

经过K-L变换后，U^TX的各个行向量依次称为第一主分量、第二主分量、…、第N主分量。U^TX的第一主分量包含了X的绝大部分能量信息。

采用式（2-31）对随机列矢量x=[x₁x₂…x_N]^T进行K-L变换，得到矢量y。容易验证y的均值矢量m_y与协方差矩阵C_y分别为

C_y是一个对角矩阵，主对角线的元素就是C_x的特征值，主对角线以外的元素为0，从而，y的各分量之间是不相关的，也就是，K-L变换能够充分去除相关性。由于λ_i也是C_x的特征值，所以C_y与C_x具有相同的特征值与特征矢量。

K-L反变换式（2-32）可以精确重建x。在很多应用中，取y的前K个分量，把其他分量置为0，得到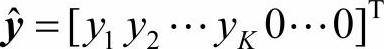，用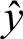来近似重建x，即

也就是，利用C_x中与K个最大特征值对应的K个特征矢量来近似重建x。容易验证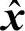，是x的无偏估计，即

并且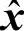，与x之间误差能量（均方误差）为

式（2-36）表明，如果K=N，即利用C_x的所有特征矢量来重建，则两者之间的均方误差为0，可得到精确重建。由于λ_j是单调递减的，因此，可以根据误差的要求来选取特征矢量的个数K，此外，通过选择对应最大特征值的K个特征矢量可以使得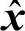与x之间的均方误差达到最小，即K-L变换是在均方误差最小意义下的最优变换。