基本原理介绍：Walsh-Hadamard变换

Walsh-Hadamard变换在图像数据压缩、滤波、编码中有广泛的应用，它可用于硬件实现，容易模拟但很难分析；它具有无乘积计算，有快速运算算法，还可由递推矩阵求得Hadamard矩阵等特点。

（1）Walsh函数

Walsh-Hadamard变换的变换核是一类非正弦的正交函数（Walsh函数），例如方波或矩形波。与正弦波频率相对应，这种非正弦波形可用“列率”（单位时间内波形通过零点数平均值的一半）描述。Walsh函数可以由Rademacher函数构成。Rademacher函数集是一个不完备的正交函数集，Rademacher函数有两个自变量n和t，用R（n，t）表示。

Rademacher函数波形图和矩阵表示：

用Rademacher函数构造Walsh函数：

其中，p表示i所选用的二进制位数R（k+1，t）是Rademacher函数；

〈i_k〉是i的自然二进制的位序反写后的第k位数字，i_k∈{1，0}。

Walsh函数的矩阵形式：

其变换核矩阵有递推关系（直积）：

（2）Walsh-Hadamard变换定义

函数f（t）的一维离散Walsh变换为：

其中，0≤i≤N-1，Walsh(i，f)为沃尔什函数，又被称为沃尔什变换核，N为采样点数。

其逆变换为：

其中0≤t≤N-1。(www.xing528.com)

一维离散沃尔什变换可表示成如下矩阵形式。

其中，H_N为N阶哈达玛矩阵。

其逆变换为：

函数f（x，y）的二维离散Walsh-Hadamard变换为

其逆变换为：

由定义可知W_xy（u，v）可以从计算W_x（u，v）的每一行的Walsh-Hadamard变换得到，结果产生N_xN_y个系数：

二维Walsh-Hadamard变换可由以下两种方法进行计算。

方法一：二维Walsh-Hadamard变换可以通过一维Walsh-Hadamard变换计算得到，步骤如下。

1）以N=N_x，对f（x，y）中N_y列中的每一列作变换，得到W_x（u，y）。

2）以N=N_y，对W_x（u，y）中N_x行中的每一行作变换，得到二维变换系数W_xy（u，v）。

方法二：将二维Walsh-Hadamard变换当做一维来计算，这种方法将数据矩阵f（x，y）的列顺序排列，这样就形成了N_xN_y个元素的列矩阵。然后按照一维Walsh-Hadamard变换方法来计算。

对下述矩阵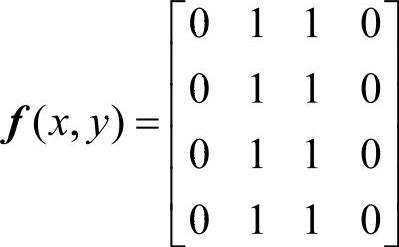进行二维Walsh-Hadamard变换的过程如下。

另外有