由于二维小波分解重构可以用一系列的一维小波分解重构来实现,我们先来讨论一维小波的分解与重构。
例程2-29是一维小波分解的MATLAB源程序,小波基采用的是Haar小波。Haar基本小波是定义在区间[0,1]上的函数,其数学表达式为:
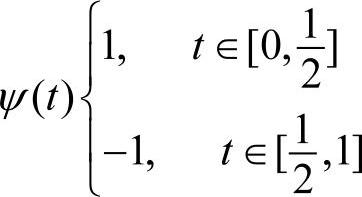
Haar小波的波形图如图2-47所示。
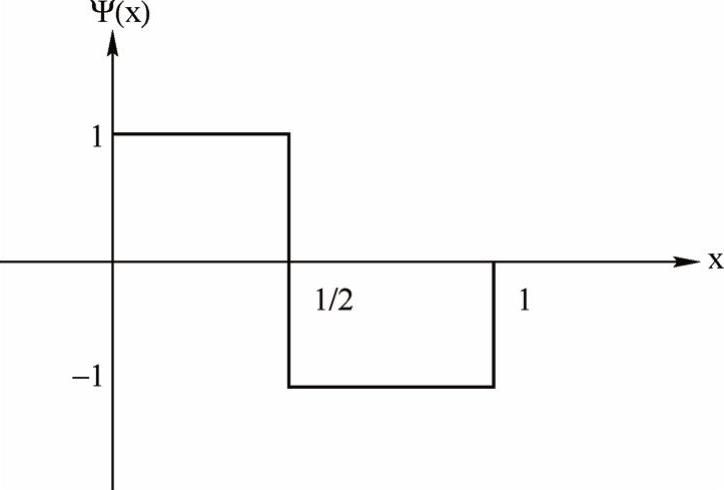
图2-47 Haar小波波形
小波变换的一级分解过程是,原始信号分别进行低通、高通滤波,再分别进行二元下抽样,就得到低频、高频(也称为平均、细节)两部分系数;而多级分解则是对上一级分解得到的低频系数再进行小波分解,是一个递归过程。
例程2-29

例程2-30是一维小波重构的MATLAB程序,小波基采用的是Haar小波。
重构则是分解的逆过程,对低频系数、高频系数分别进行上抽样和低通、高通滤波处理。要注意重构时同一级的低频、高频系数的个数必须相等。
例程2-30


二维小波分解重构可以用一系列的一维小波分解重构来实现。例程2-31和例程2-32是基于Haar小波的二维小波分解和重构过程。
例程2-31

例程2-32

为了实现图像的N层分解,对一幅m行n列的黑白图像要对其进行规范化处理,使其能被2的N次方整除。例程2-33便实现了该功能。
例程2-33


将规范化后的图像的数据格式由适合显示图像的uint8格式转换为适合数值处理的double格式,再调用二维小波分解函数进行图像分解,最后为了清晰地显示分解图像的塔式结构,在图像的相应区域绘制若干分界线。具体程序如例程2-34所示。
例程2-34


上述的图像分解程序,其输出数据是double型,以便作为重构程序的输入。例程2-34的运行过程如图2-48所示,其结果如图2-49所示。(https://www.xing528.com)

图2-48 例程2-34运行过程

图2-49 例程2-34的运行结果
接下来讨论图像的重构,在编写的重构程序中(例程2-35),为了比较分解图像和重构图像,首先绘出经过小波分解的图像,然后再进行重构。在绘制分解图像和重构图像的过程中,要注意数据格式的转换。
例程2-35


例程2-35的运行过程如图2-50所示,运行结果如图2-51所示。

图2-50 例程2-35的运行过程

图2-51 例程2-35的运行结果
a)小波重构的过程 b)小波重构后的图像
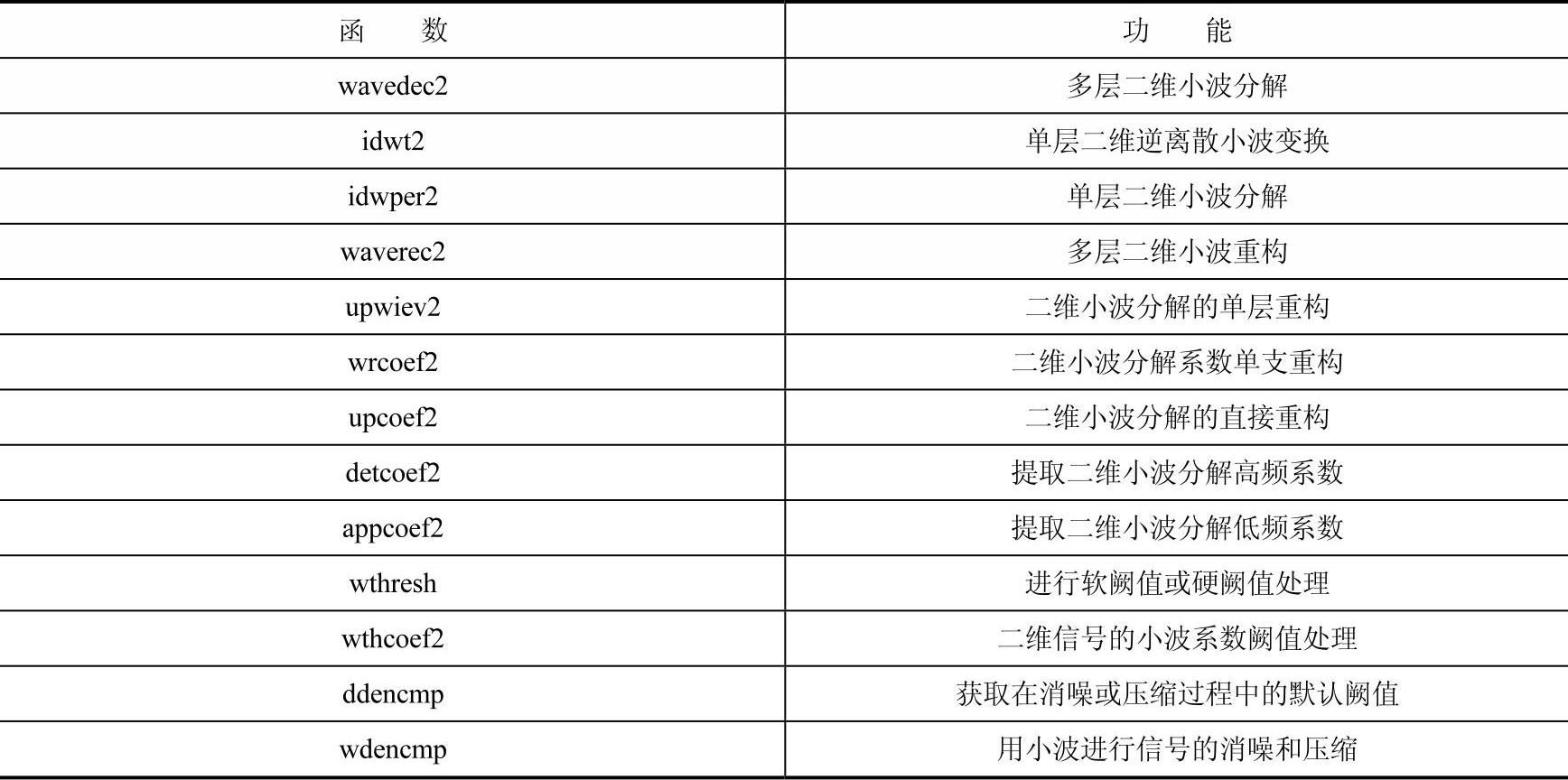
在MATLAB7.0中有专门的小波函数工具箱,支持小波在图像处理中的应用,表2-2和表2-3主要列出了小波函数工具箱中的一维、二维小波应用函数。
例程2-36是调用小波工具箱中的二维小波处理函数进行小波分解和重构的MATLAB源程序,其运行结果如图2-52所示。
表2-2 一维离散小波函数
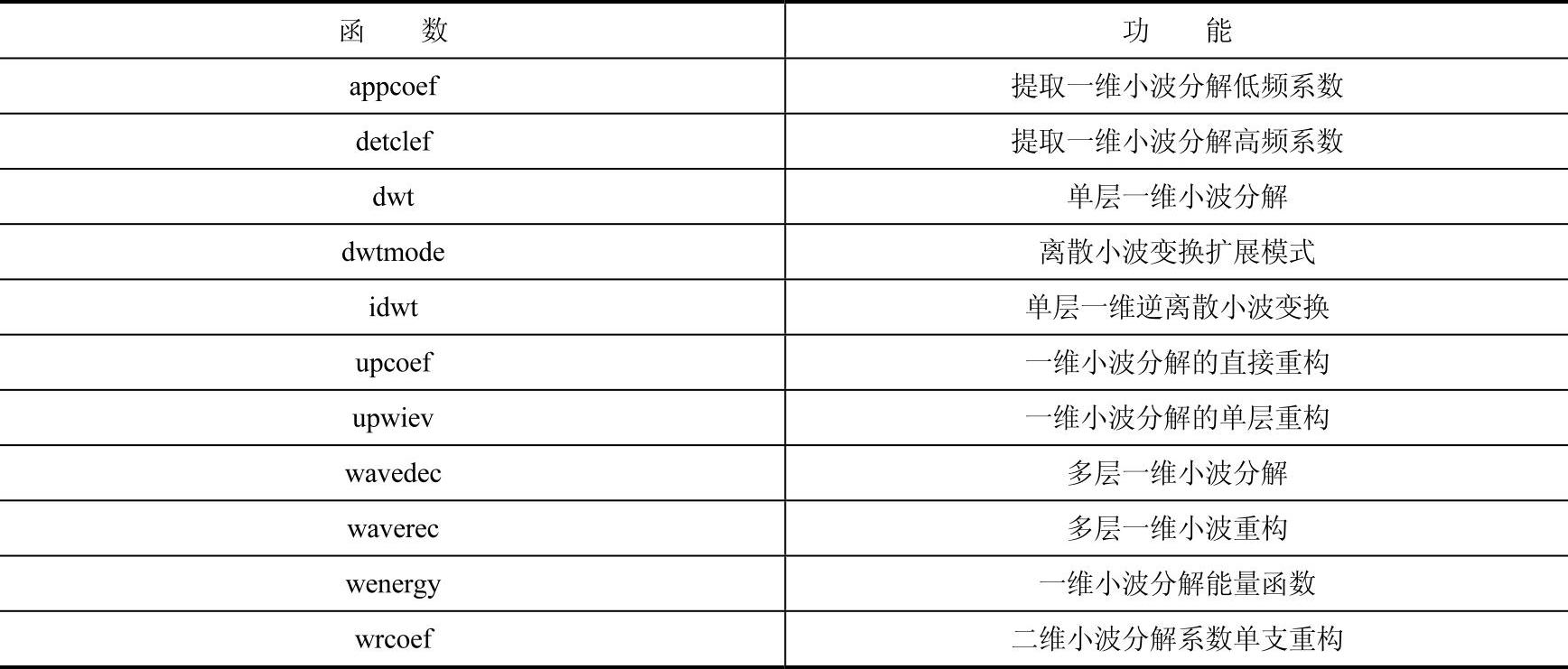
表2-3 二维离散小波函数

(续)
例程2-36


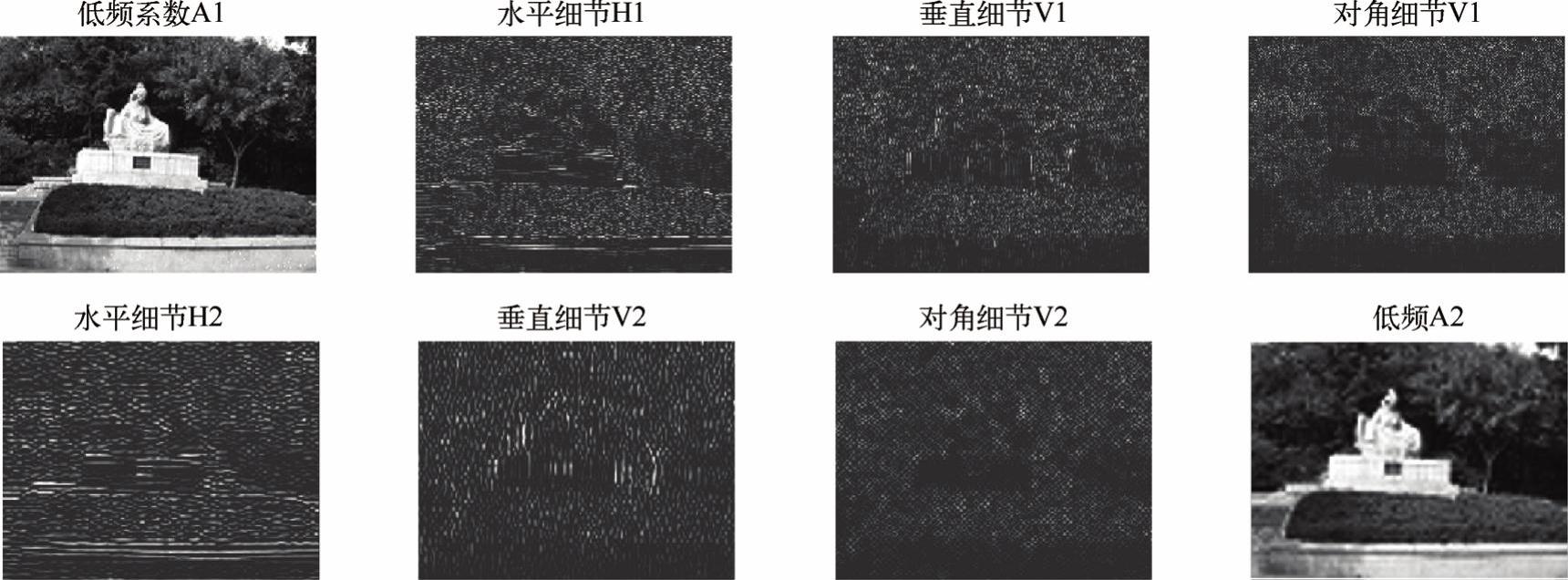
图2-52 小波分解和重构
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




