小波变换的步骤及特点简介

一维信号小波变换的步骤如下，通过对一维信号小波变换步骤的详细讲解，希望读者对小波变换的实现过程有更加深入的认识。

1）选择一个小波函数，并将这个小波与要分析的信号起始点对齐。

2）计算在这一时刻要分析的信号与小波函数的逼近程度，即计算小波变换系数C，C越大，就意味着此刻信号与所选择的小波函数波形越相近，如图2-44所示。

3）将小波函数沿时间轴向右移动一个单位时间，然后重复步骤1）和步骤2）求出此时的小波变换系数C，直到覆盖完整个信号长度，如图2-45所示。

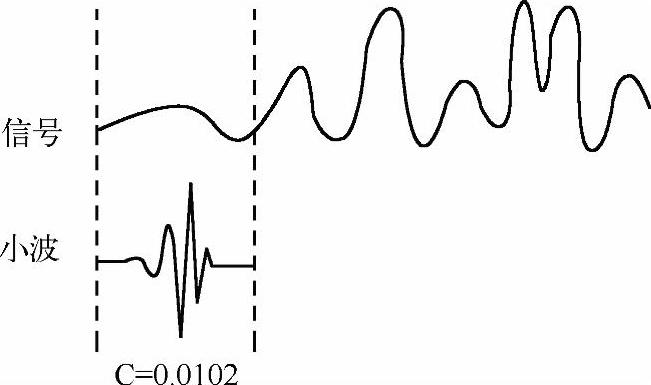
图2-44 步骤①、②示意图

4）将所选择的小波函数尺度伸缩一个单位，然后重复步骤1）～步骤3）操作，如图2-46所示。

图2-45 步骤③示意图

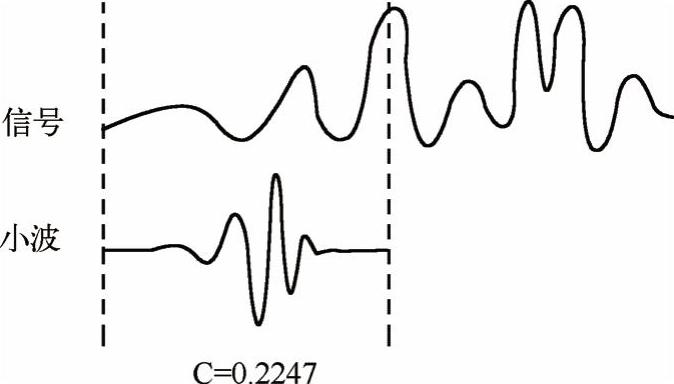
图2-46 步骤④示意图(www.xing528.com)

5）对所有的尺度伸缩重复步骤1）～步骤4）。

二维小波分解重构可以用一系列的一维小波分解重构来实现。

在小波变换中，尺度与频率的关系如下。

➢小尺度a→压缩的小波→快速变换的细节→高频部分。

➢大尺度a→拉伸的小波→缓慢变换的粗部→低频部分。

对于数字图像处理，小波变换大致可以总结出以下4个特点，这些特点使得小波变换比较适合于对图像进行压缩、去噪、融合等。

➢小波变换的多分辨率特性可以对图像进行不同尺度的分解，从而可以获取目标图像不同层次的轮廓信息和细节信息，而且对在某个尺度的轮廓进行更小尺度的分解时，可以呈现出更小尺度的轮廓信息和细节信息。

➢小波变换较之于其他几种正交变换在运算速度上要快，而且小波变换对图像的分解呈Mallat塔式分解，此分解方程及其滤波器系数对任意两相邻尺度均保持恒定。另外，小波变换还具有集中信号能量的能力，这使得经小波变换后图像信息只集中在少数几个变换系数上，这在一定程度上也有助于降低小波变换在时间和空间上的复杂度。

➢小波变换在增加图像分解层次时并没有引起数据量的增加，由于信号在小波变换域中主要集中在少数系数上，因此如果考虑通过模极大值来精确近似原始信号，还能减少小波变换后的数据量。

➢由于图像信号突变点和噪声对小波系数敏感性不同，使得小波变换在图像去噪处理中也有较好的应用效果。