离散小波变换简介

在数值计算中，需要对小波变换的尺度因子、位移因子进行离散化，一般采用如下的离散化方式。

令尺度因子a=a₀^m，b=ka₀^mb₀（其中a＞1，b≠0，m，n为整数），小波基函数为

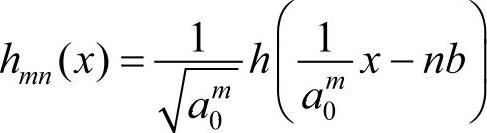
适当选择h，a₀，b₀使h_mn（x）构成规范正交基。

通常采用a₀=2，b₀=1构成离散二进小波。例如，在平方可积函数空间L²（R）中，最典型的规范正交基是Haar基，取a₀=2，b₀=1时，小波函数族为

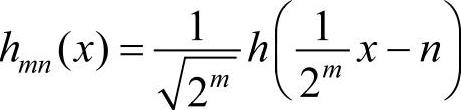
（1）多分辨分析

基本小波通过伸缩构成一组基函数，在大尺度上，膨胀的基函数搜索大的特征，而在较小的尺度上，它们则寻找细节信息。

（2）快速小波变换算法（FWT）

利用双带子带编码迭代，自底向上建立小波变换。首先按照低半带和高半带进行子带编码后，对低半带再一次进行子带编码，得到一个N/2点的高半带信号和对应于区间[0，s_N]的第一和第二个1/4区域的两个N/4点的子带信号。然后，连续进行上述过程，每一步都保留高半带信号并进一步编码低半带信号，直到得到一个仅有一个点的低半带信号为止。这样，小波变换系数就是这个低半带点再加上全部用子带编码的高半带信号。最前面的N/2个系数来自于F（s）的高半带，接下来N/4个点来自于第二个1/4带，依次类推。图2-39给出了离散小波变换算法的处理流程。

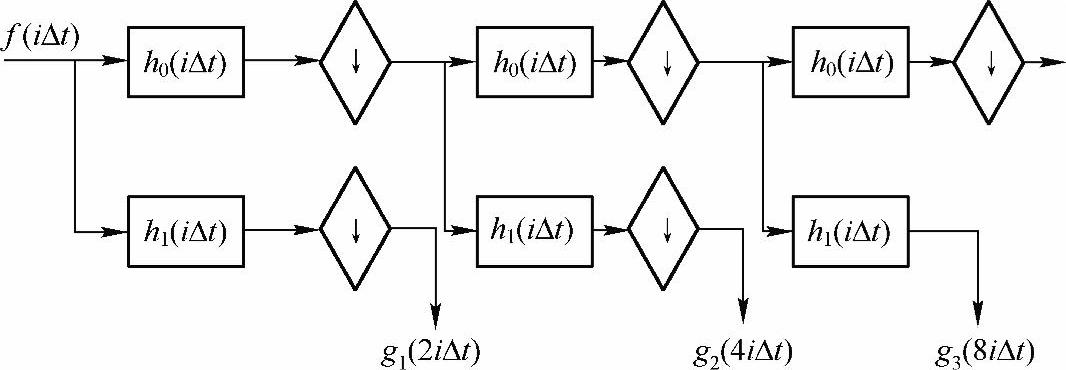
图2-39 离散小波变换算法

上述算法被称为快速小波变换（Fast Wavelet Transform，FWT），也因其形状而被称为“鱼骨型算法”，其逆变换如图2-40所示。

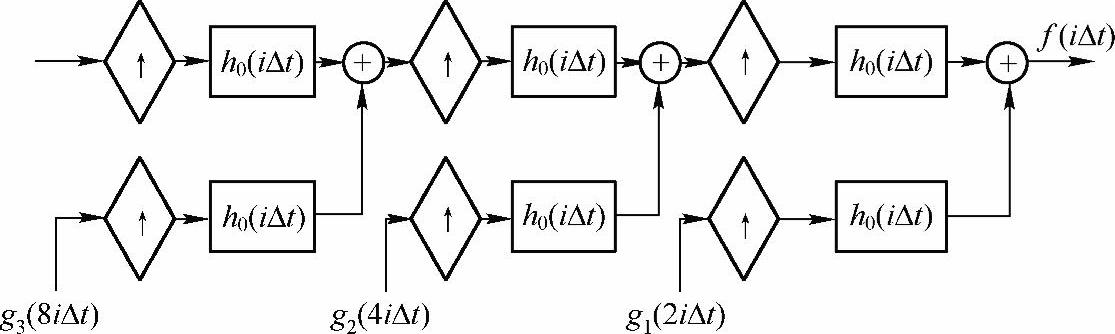
图2-40 离散小波逆变换算法

（3）离散小波变换的设计

根据子带编码重构公式，在频率域上有

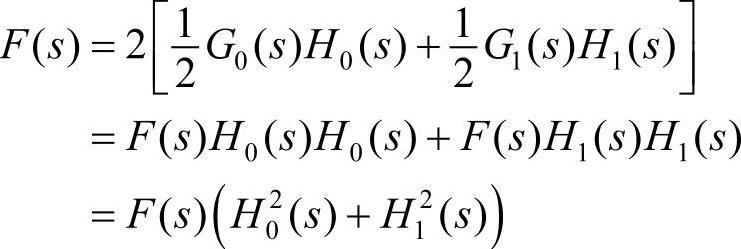
所以，双通道子带编码的两个滤波器必须满足条件：

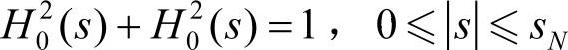
假设H₀（s）是小波变换中使用的具有平滑边缘的低通滤波传递函数，则相应的H₁（s）需按下式给出。

H₁²（s）=1-H₀²（s）

可见，设计一个离散小波变换的任务就是精心挑选低通滤波器。我们称符合这一条件的离散低通滤波器脉冲响应h₀（s）为尺度向量，由它产生一个有关的函数称为尺度函数。尺度向量和尺度函数彼此互相确定。

例如，由尺度向量h₀（k）到尺度函数的定义如下。

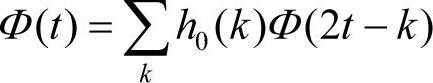
它可以通过自身半尺度复制后的加权和来构造。另外它也能用带尺度的矩形脉冲函数卷积h₀（k）后再利用数值计算方法得到：

(www.xing528.com)

其中，

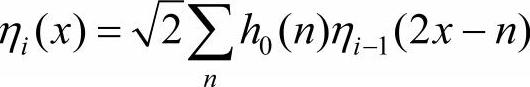
相反，由尺度函数开始，在它满足单位平移下正交归一条件时，尺度向量的计算方法如下。

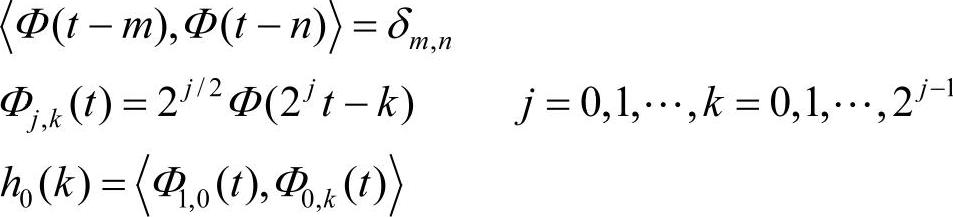
（4）二维离散小波变换

为了将一维离散小波变换推广到二维，只考虑尺度函数是可分离的情况，即

Φ（x，y）=Φ（x）Φ（y）

式中，Φ（x）是一维尺度函数，其相应的小波是Ψ（x），下列3个二维基本小波是建立二维小波变换的基础：

Ψ¹（x，y）=Φ（x）Ψ（y），Ψ²（x，y）=Φ（y）Ψ（x），Ψ³（x，y）=Ψ（x）Ψ（y）

它们构成二维平方可积函数空间L²（R²）的正交归一基：

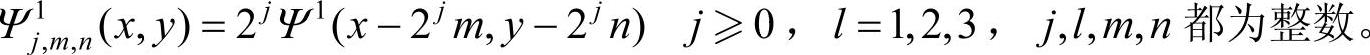
从一幅N×N的图像f（x，y）开始，其中上标指示尺度并且N是2的幂。对于j=0，尺度2^j=2⁰=1，也就是原图像的尺度。j值的每一次增大都是尺度加倍，而使分辨率减半。在变换的每一层次，图像都被分解为4个1/4大小相同的图像，它们都是由原图与一个小波基图像的内积后，再经过在行和列方向进行2倍的间隔抽样而生成的。对于第一个层次（j=1），可写成

后续的层次（j＞1），依次类推，形成如图2-41所示的形式。

若将内积改写成卷积形式则有：

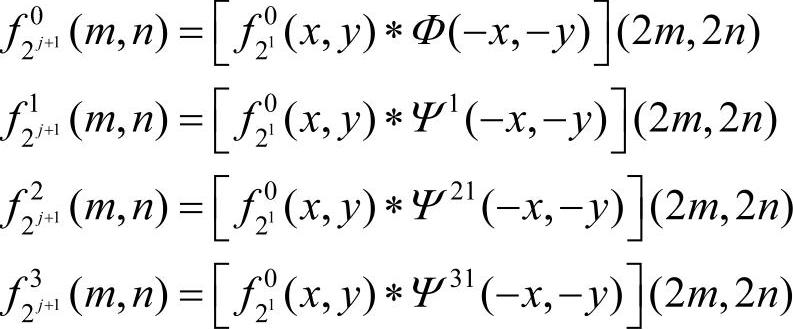
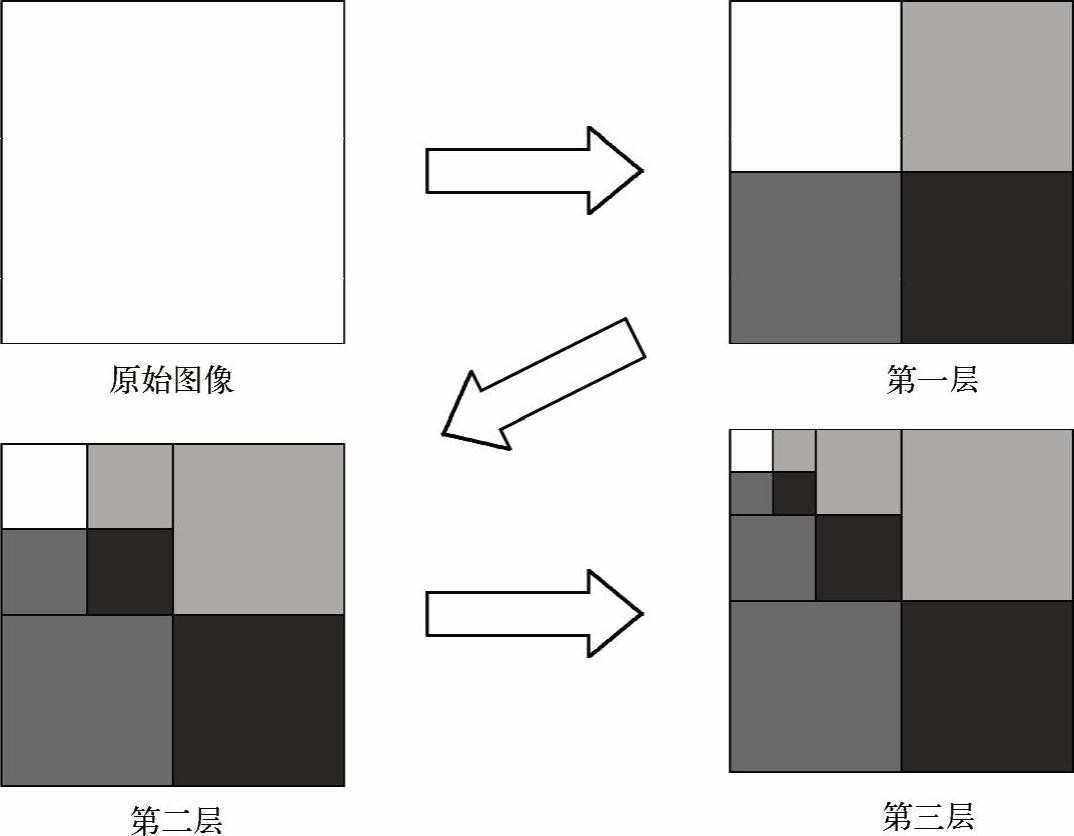
图2-41 二维离散小波变换

因为尺度函数和小波函数都是可分离的，所以每个卷积都可分解成行和列的一维卷积。例如，在第一层，首先用h₀（-x）和h₁（-x）分别与图像f（x，y）的每行作卷积并丢弃奇数列（以最左列为第0行）。接着这个（N×N）/2矩阵的每列再和h₀（-x）和h₁（-x）相卷积，丢弃奇数行（以最上行为第0行）。结果就是该层变换所要求的4个（N/2）×（N/2）的数组，如图2-42所示。

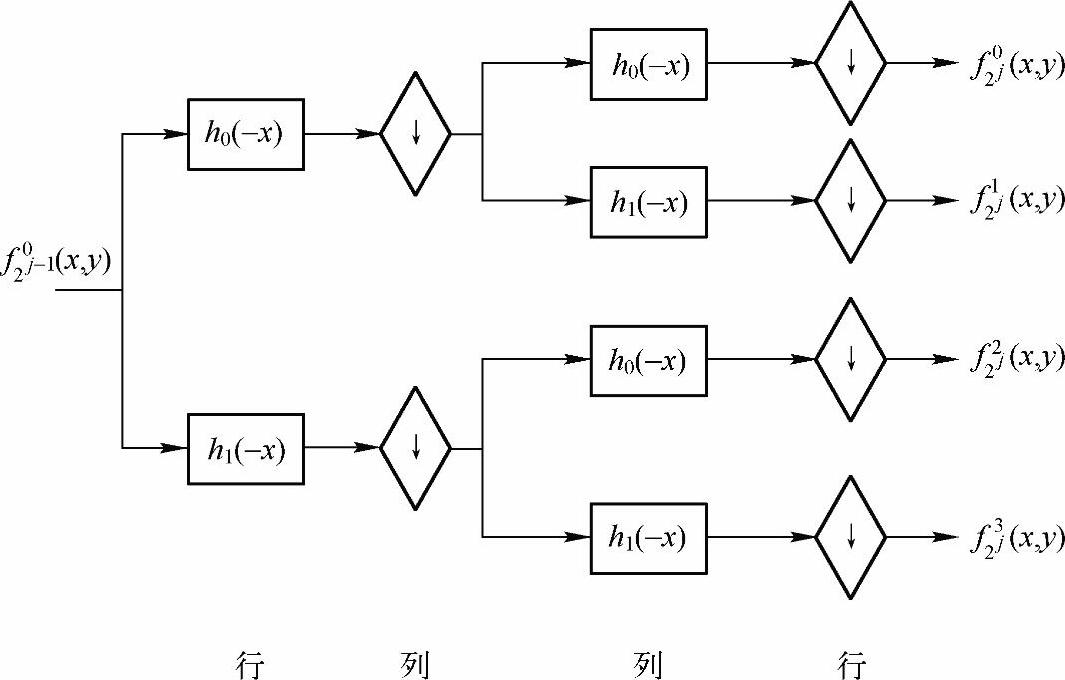
图2-42 DWT图像分解步骤

离散小波逆变换与上述过程相似，在每一层，通过在每一列的左边插入一列零来增频采样前一层的4个矩阵；接着用h₀（x）和h₁（x）来卷积各行，再成对地把这几个N/2×N的矩阵加起来；然后通过在每行上面插入一行0来将刚才所得的两个矩阵增频采样为N×N；再用h₀（x）和h₁（x）与这两个矩阵的每列卷积。这两个矩阵的和就是这一层重建的结果。

图2-43给出了逆小波变换图像重建的过程。

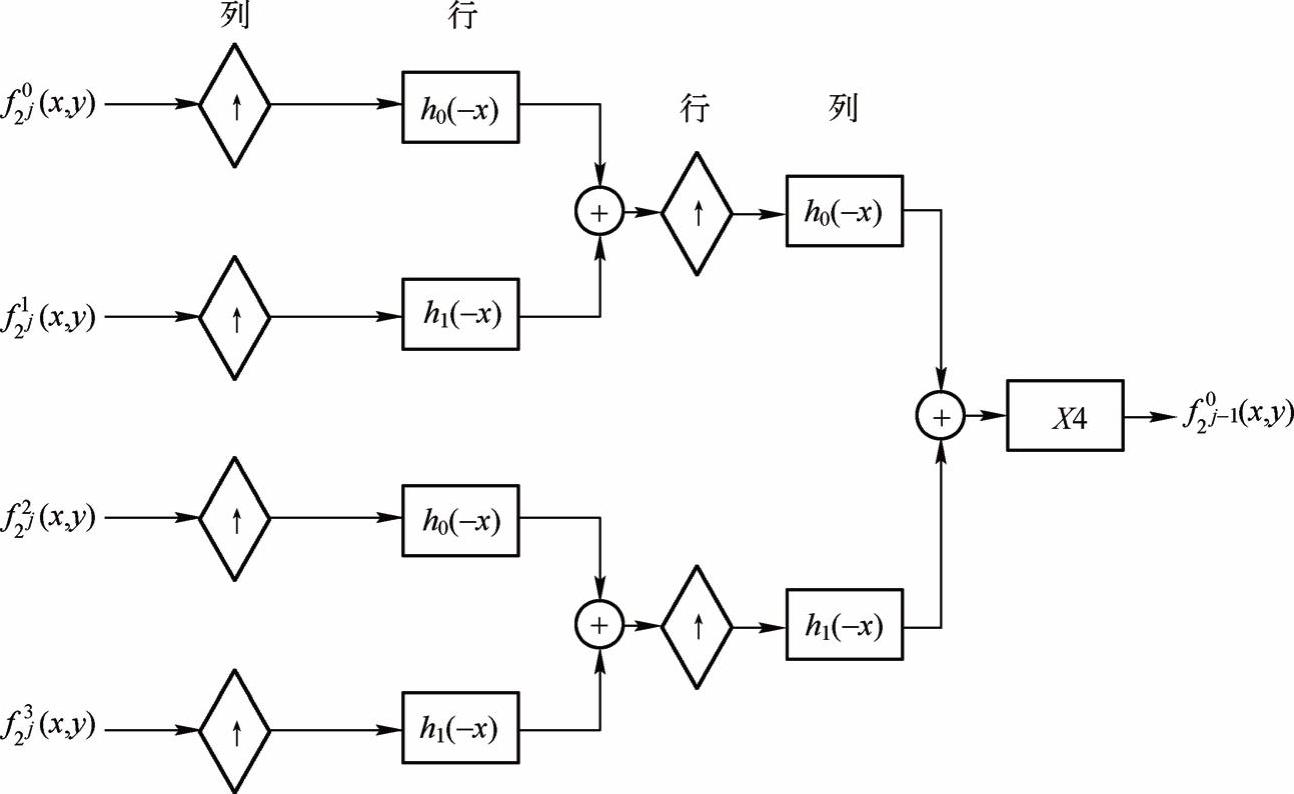
图2-43 DWT图像重建步骤