小波分析的起源及发展历程

小波分析（Wavelet Analysis）是20世纪80年代中期发展起来的一门数学理论和方法，它是由法国科学家Grossman和Morlet在进行地震信号分析时提出的，随后得到迅速发展。1985年Meyer在一维情形下证明了小波函数的存在性，并在理论上作了深入的研究。Mallat基于多分辨分析的思想，提出了对小波应用起重要作用的Mallat算法，它在小波分析中的地位相当于FFT在经典傅里叶变换中的地位。小波分析理论的重要性及应用的广泛性引起了科技界的高度重视，小波分析的出现被认为是傅里叶分析的突破性进展。科研工作者在逼近论、微分方程、模识识别、计算机视觉、图像处理、非线性科学等方面使用小波分析取得了许多突破性进展。

小波变换的基本思想类似于傅里叶变换，就是用信号在一簇基函数形成空间上的投影表征该信号。经典的傅里叶变换把信号按正弦基展开，将任意函数表示为具有不同频率的谐波函数的线性叠加，能较好地描述信号的频率特性；但它在时域上无任何分辨，不能作局部分析。这在理论和应用上都限制了傅里叶变换的发展。小波变换在时域和频域同时具有良好的局部化性能，有一个灵活可变的时间-频率窗，它与傅里叶变换相比，能更有效地从信号中提取信息，通过伸缩和平移等运算功能对函数或信号进行多尺度细化分析（Multiscale Analysis），解决了傅里叶变换不能解决的许多问题，因而，小波变换被誉为是“数学显微镜”，它是信号处理发展史上的里程碑。

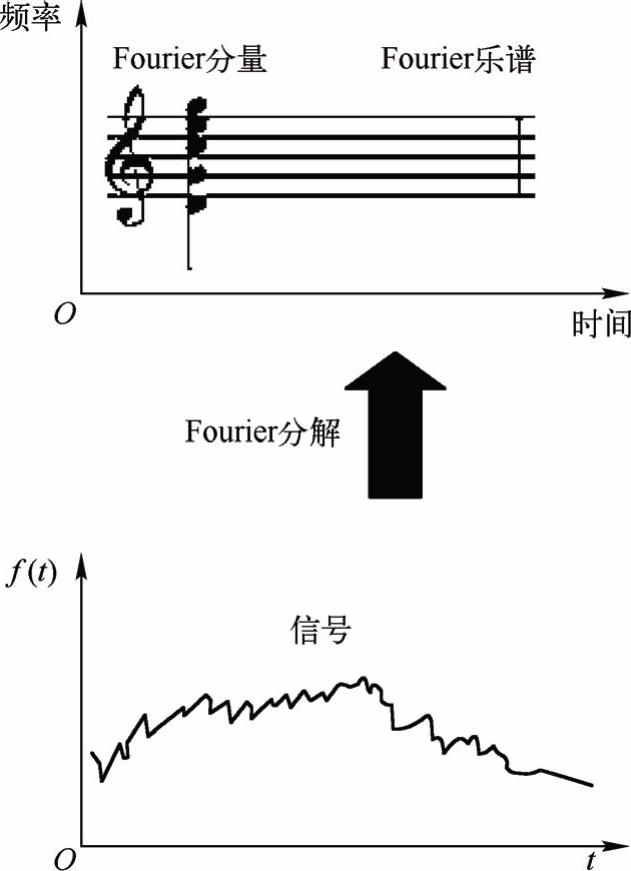
这里通过一个例子来说明傅里叶变换与小波变换的联系和区别。歌声是一种声音振荡的波函数，其傅里叶变换就是将这个波函数转化成某种乐谱。但遗憾的是，傅里叶变换无法反映信号在哪一时刻有高音，在哪一时刻有低音，因此结果是所有的音符都挤在了一起，如图2-37所示。

小波变换有效地克服了傅里叶变换的这一缺点，信号变换到小波域后，小波不仅能检测到高音与低音，而且还能将高音与低音发生的位置与原始信号相对应，如图2-38所示。

小波分析的应用是与小波分析的理论研究紧密地结合在一起的。现在，它已经在科技信息产业领域取得了令人瞩目的成就。从数学角度来看，信号与图像处理可以统一看做是信号处理（图像可以看做是二维信号），小波分析的许多应用都可以归结为信号处理问题。现在，对于性质随时间变化而稳定不变的信号，处理的理想工具仍然是傅里叶分析。但是实际应用中的绝大多数信号是非稳定的，而适用于处理非稳定信号的工具就是小波分析。

由于小波分析可以将信号或图像分层按小波基展开，可以根据图像信号的性质和事先给定的处理要求展开到特定的级数，这样不仅可以有效地控制计算量，满足实时处理的需要，而且还可以方便地实现累进传输编码。同时，小波变换具有放大、缩小和平移的数学显微镜的功能，能够很方便地产生各种分辨率的图像，从而适用于不同分辨率图像的I/O设备和不同传输速率的通信系统。

(www.xing528.com)

图2-37 歌声信号与傅里叶分解

图2-38 歌声信号与小波分解

由于小波分析具有以上这些优点，所以在最近颁布的运动图像压缩标准MPEG4中，其中的视觉纹理模式是基于零高度树的小波算法实现的。该模式在非常宽的比特率范围内具有很高的编码效率，除了具有很高的压缩效率之外，它还提供了空间和质量的可缩放性。

综上所述，由于小波变换克服了傅里叶变换的许多弱点，它不仅可以用于图像压缩，还可以用于其他领域，如信号分析、静态图像识别、计算机视觉、声音压缩与合成、视频图像分析、CT成像、地震勘探和分形力学等。