空域滤波的分类与常用方法

空域滤波是指借助模板对图像进行邻域操作，输出图像每一个像素的取值都是根据模板对输入像素相应邻域内的像素进行计算得到的。根据其特点，空域滤波一般可以分为线性和非线性两类处理方法；按照其功能，可以分为平滑滤波器和锐化滤波器。平滑滤波器主要实现模糊和去除噪声。模糊主要是在提取较大目标前，去除太小的细节或将目标内的小间断连接起来。锐化滤波器是为了增强被模糊的细节边缘。

空域滤波都是基于模板卷积的，对图像中任意的像素点（x，y）进行m×n掩模处理得到的响应为：

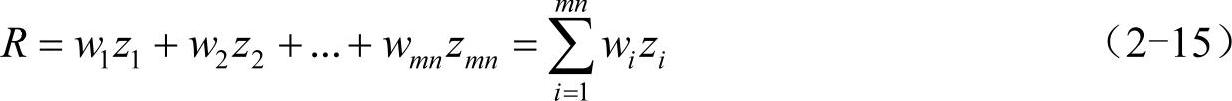
其中，w为掩模系数，z为与该系数对应的像素灰度值，mn为掩模中包含的像素总数。将模板在图像上游历遍历，对每个像素都采用模板进行运算，就可以按照模板性质的不同，实现不同的功能。该过程称为基于模板的卷积。

基于模板卷积的空域滤波的主要步骤为：

1）将模板在图像中移动，并将模板中心与图像中的某个像素位置重合。

2）读取模板下各对应像素的灰度值和，并与模板的系数相乘。

3）将所有的乘积相加。

4）将和赋值给模板中对应位置的像素。

下面介绍几种常用的空域滤波方法。

（1）邻域平均法

邻域平均法是最简单的空域处理方法，属于线性滤波器，其基本思想是利用几个像素灰度的平均值代替每个像素的灰度。对于位置（i，j）处的像素，其灰度值为f（i，j），平滑后的灰度值为g（i，j），则g（i，j）由包含（i，j）领域的若干个像素的灰度平均值所决定，即用（2-16）式得到平滑的像素灰度值

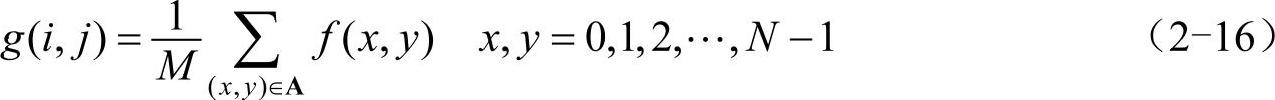
式中，A表示以（i，j）为中心的领域点的集合，M是A中像素点的总数。图2-24表示了4个邻域点和8个邻域点的集合。

图2-24 邻域平均法示意图

a）4个邻域点的集合 b）8个邻域点的集合

邻域平均法的平滑效果与所使用的邻域半径大小有关。半径越大，平滑图像的模糊程度越大。邻域平均法的优点在于算法简单、计算速度快，主要缺点是在降低噪声的同时使图像产生模糊，特别是在边缘和细节处，邻域越大，模糊越厉害。为了尽可能减少模糊失真，有人提出了“超限邻域平均法”，也就是采用下列准则形成平滑图像。

式中，T是一个规定的非负阈值，可以根据图像总体特性或者局部特性确定。当一些点和它们邻域的差值超过规定的T阈值时，才进行噪声处理，否则仍保留这些点的像素灰度值。邻域取得越大，像素点越多，则信噪比提高越大，平滑效果越好，但是图像模糊也越严重。邻域平均是以图像模糊为代价来换取噪声的减少的。

例程2-20是实现邻域平均法的MATLAB程序，其运行结果如图2-25所示。

例程2-20

图2-25 例程2-20的运行结果

a）原始图像 b）滤波之后的图像

在MATLAB中，可以通过如下指令实现邻域均值滤波。

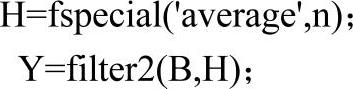
其中，n为邻域的大小，B为待滤波的二维灰度图像矩阵，H为所构造的邻域均值滤波器。

例程2-21是对图像人为添加了椒盐噪声，然后利用不同大小掩模的均值滤波器对噪声进行处理的程序，其运行结果如图2-26所示。

例程2-21

图2-26 例程2-21的运行结果

a）添加噪声后的图像 b）3×3邻域滤波结果 c）5×5邻域滤波结果 d）7×7邻域滤波结果

从例程2-21的运行结果可知，均值滤波去噪时，模板大小的选取至关重要。一般来说，模板越大，去噪能力就越强，但同时也会使图像变得模糊。原因在于：均值滤波时采用了平均操作，图像数据本身也会因为平均而变得模糊。

（2）加权均值滤波

为了克服简单局部平均的弊病，目前已经研究提出了许多保留边缘细节的局部平滑算法，它们讨论的重点都在如何选择领域的大小、形状和方向，如何选择参加平均的点数以及邻域各点的权重系数等。把这类根据参与平均像素的特点赋予不同权值的方法称为加权均值滤波，常用的有灰度最近K个邻点平均法、梯度倒数加权平滑、最大均匀性平滑、小斜面模型平滑等。

一般来讲，可以按照下列准则来确定参与平均的各像素的权值。

➢待处理的像素赋予较大的权值，其他像素的权值均较小。

➢按照距离待处理像素的远近确定权值，距离待处理像素较近的像素赋予较大的权值。

➢按照与待处理像素的灰度接近程度确定权值，与待处理像素灰度较接近的像素赋予较大的权值。

为了不使整个图像在平滑后变亮，需要将权值进行归一化处理。下面介绍一种最常见的加权平均法—梯度倒数加权法。

在一幅数字图像中，相邻区域的变化大于区域内部的变化，同一区域内部中间像素的变化小于边缘像素的变化。在图像变化缓慢的区域，灰度梯度值小；在图像变化较快的区域，灰度梯度值大。当以灰度梯度倒数作为权值时，区域内部的邻点像素的权值就比区域边缘或者区域外的邻点像素的权值大。此时平滑的贡献主要来自区域内部的像素，平滑后图像边缘和细节不会受到明显损害。这就是梯度倒数加权法的基本思想。

假设像素点（i，j）的灰度值为f（i，j），取该像素的3×3的领域窗口，其像素组成为(www.xing528.com)

以灰度梯度倒数构成的权值矩阵为

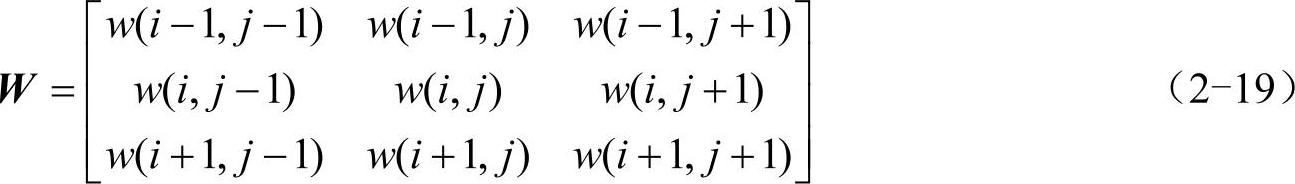
式中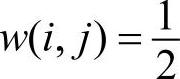，，权值矩阵其他元素为

式中，m，n分别为-1，0，1，且不能同时为0。

平滑输出为窗口像素分别与对应位置上的权值相乘，即

此外，下面的模板也是常见的加权平均滤波模板。

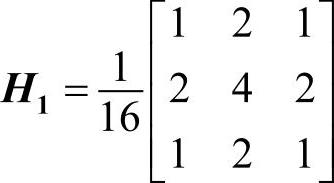
例程2-22是采用加权平均滤波模板H₁对输入图像进行加权平均滤波的MATLAB源程序，运行结果如图2-27所示。

例程2-22

图2-27 例程2-22的运行结果

a）添加噪声后的图像 b）滤波后的结果

（3）中值滤波

如果既要消除噪声又要保持图像的细节，可以使用中值滤波。中值滤波器是一种非线性平滑滤波器。它的主要功能是让与周围像素灰度值的差比较大的像素改变，并取与周围像素相近的值，从而消除孤立的噪声点。它的主要步骤为：

1）将模板在图像中移动，并将模板中心与图像中的某个像素位置重合。

2）读取模板下各对应像素的灰度值。

3）将这些灰度值从小到大排成一列。

4）找出这些值里排在中间的一个。

5）将这些中间值赋值给对应模板中心位置的像素。

二维中值滤波器的窗口形状可以有多种，如线状、方形、十字形、圆形、菱形等，如图2-28所示。不同形状的窗口产生不同的滤波效果，使用中必须根据图像的内容和不同

图2-28 二维中值滤波器常用窗口形状

的要求加以选择。从以往的经验来看，对于有缓变的较长轮廓线物体的图像，采用方形或者圆形窗口比较适宜；对于包含有尖顶角物体的图像，则适宜采用十字形窗口。使用二维中值滤波最值得注意的就是保持图像中有效的细线状物体。

例程2-23利用中值滤波去噪的MATLAB例程。

例程2-23

例程2-23的运行结果如图2-29所示。中值滤波较好地去除了椒盐噪声，且避免了均值滤波所带来的图像模糊现象。

图2-29 例程2-23的运行结果

a）添加噪声后的图像 b）滤波后的结果

MATLAB数字图像处理工具箱提供了medfilt2（）函数来实现图像的二维中值滤波，其用法如下。

B=medfilt2（A，[mn]）；

其中，A为输入图像矩阵，B是中值滤波后输出的结果，[mn]用于指定滤波模板的大小，如果不设置，则默认为3×3。

例程2-24是调用medfilt2（）函数来实现图像的二维中值滤波的MATLAB源程序，其运行结果如图2-30所示。

例程2-24

图2-30 例程2-24的运行结果

a）添加噪声后的图像 b）滤波后的结果