二维傅里叶变换的应用：相位相关分析

相关（correlation），顾名思义，就是两个事物的相关性。在信号处理中，两个信号的卷积就是相关，可以用于表征两个信号的相似程度。

关于图像的相位，我们知道，图像的频率域（傅里叶频谱）包含了模（amplitude）和相位（phase）信息，模包含图像整体的灰度级信息，而相位信息包含了图像变化的信息。可以说，相位是图像的DNA，不同图像，模有可能是相同的，但相位却是不同的。利用这一点，求取相位的相关，就可以知道图像之间的差别。

由于相关是通过卷积进行计算的，计算量大，所以，一般都先通过傅里叶频谱的内积，然后再做一次傅里叶逆变换就可以求取相位相关。

相位相关用于估计图像的偏移量是由C.D.Kuglin和D.C.Hines在1975年提出的。

设图像f₂（x，y）为图像f₁（x，y）分别沿x轴和y轴平移x₀和y₀后得到的图像，即：

f₂（x，y）=f₁（x-x₀，y-y₀）

则它们的傅里叶变换满足下列关系：

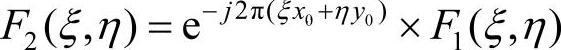
图像f₁（x，y）和f₂（x，y）的互功率谱定义为：

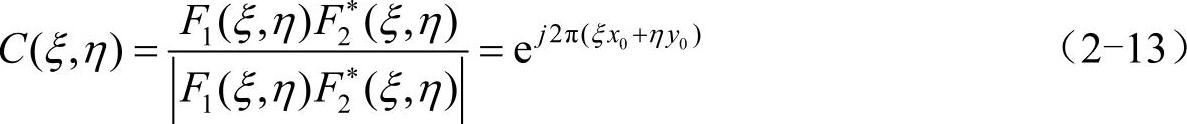
式中，F^∗为F的复共轭，式（2-13）表示两图像f₁（x，y）和f₂（x，y）的相位差与互功率谱的相位相等。对式(2-13)进行傅里叶反变换，则有：

c(x，y)=δ(x-x₀，y-y₀)

式中，c(x，y)是位于(x₀，y₀)的冲击函数，可求得两图像间的平移量x₀和y₀。

如果两幅图像是一致的（完全相同），那么它们的相位相关就是一个脉冲函数，脉冲位置在坐标原点，高度为1。(www.xing528.com)

如果两幅图像不一致，那么，在相位相关的矩阵里，最高的那个脉冲坐标就是两幅图像的位置偏移量，而脉冲的高度也会小于1。

利用相位相关求两幅图像偏移量的MATLAB源程序如例程2-13所示，其运行结果如图2-19所示。

例程2-13

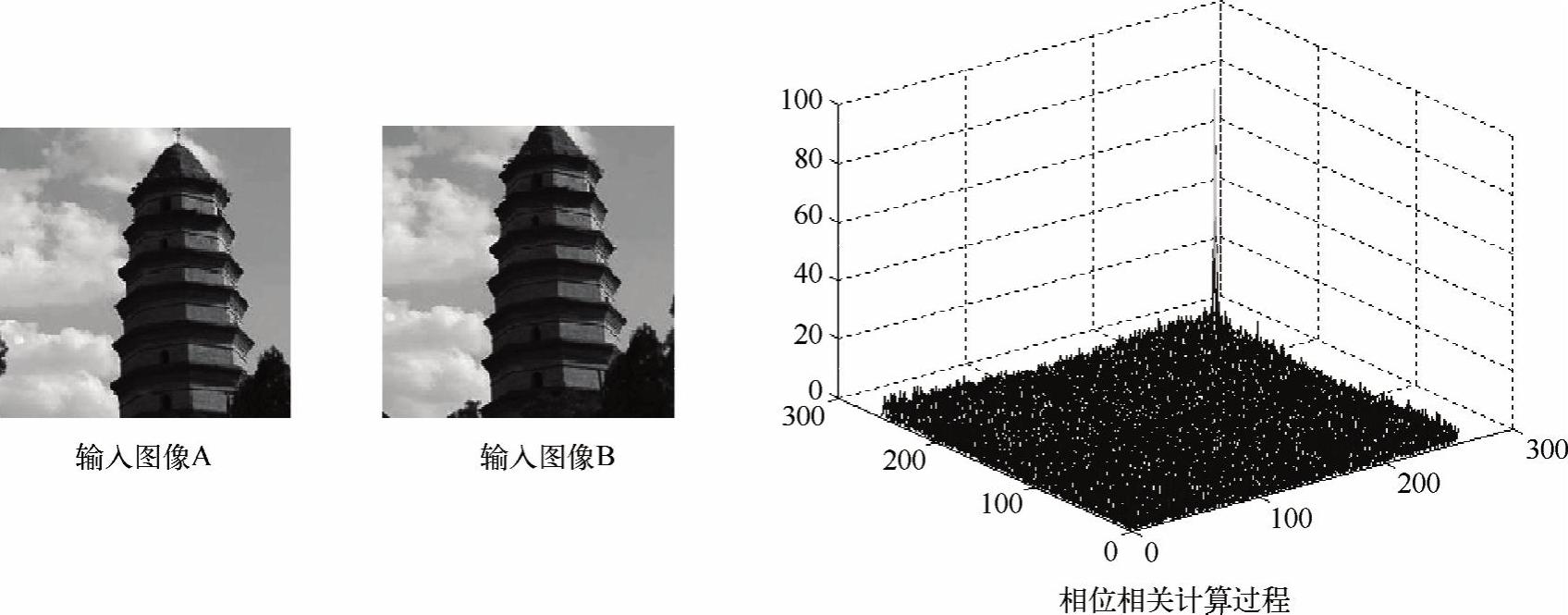
图2-19 例程2-13的运行及其结果

相位相关主要用于图像配准（image registration），由于相位信号避免了图像中低频噪音的影响，在光照条件变化的应用环境表现突出，被广泛应用于遥感、医学图像等领域。

经验分享：如何理解图像的傅里叶变换

从纯粹的数学意义上看，傅里叶变换是将一个函数转换为一系列周期函数来处理的过程。

从物理效果上看，傅里叶变换是将图像从空间域转换到频率域，其逆变换是将图像从频率域转换到空间域。换句话说，傅里叶变换的物理意义就是将图像的灰度分布函数变换为图像的频率分布函数，傅里叶逆变换是将图像的频率分布函数变换为灰度分布函数。

图像的频率是表征图像中灰度变化剧烈程度的指标，是灰度在平面空间上的梯度。例如，大面积的沙漠在图像中是一片灰度变化缓慢的区域，对应的频率值很低；而对于地表属性变换剧烈的边缘区域，它在图像中是一片灰度变化剧烈的区域，对应的频率值较高。

因此，将一幅图像进行傅里叶变换后，就将图像中的高频信息和低频信息在频率域中分开了，方便对图像进行各种处理，如进行图像平滑、边缘提取等操作。