设阵列[f(m,n)]M×N⇔[F(k,l)]M×N,[g(m,n)]M×N⇔[G(k,l)]M×N,则其具有以下性质。
(1)延拓周期性
f(m,n)=f(m+aM,n+bN)
F(k,l)=F(k+aM,l+bN)
式中,m,k=0,1,…,M-1;n,l=0,1,…,N-1;a,b为整数。这是因为 和
和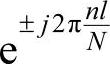 是m,n或k,l的周期函数,周期分别为M和N。
是m,n或k,l的周期函数,周期分别为M和N。
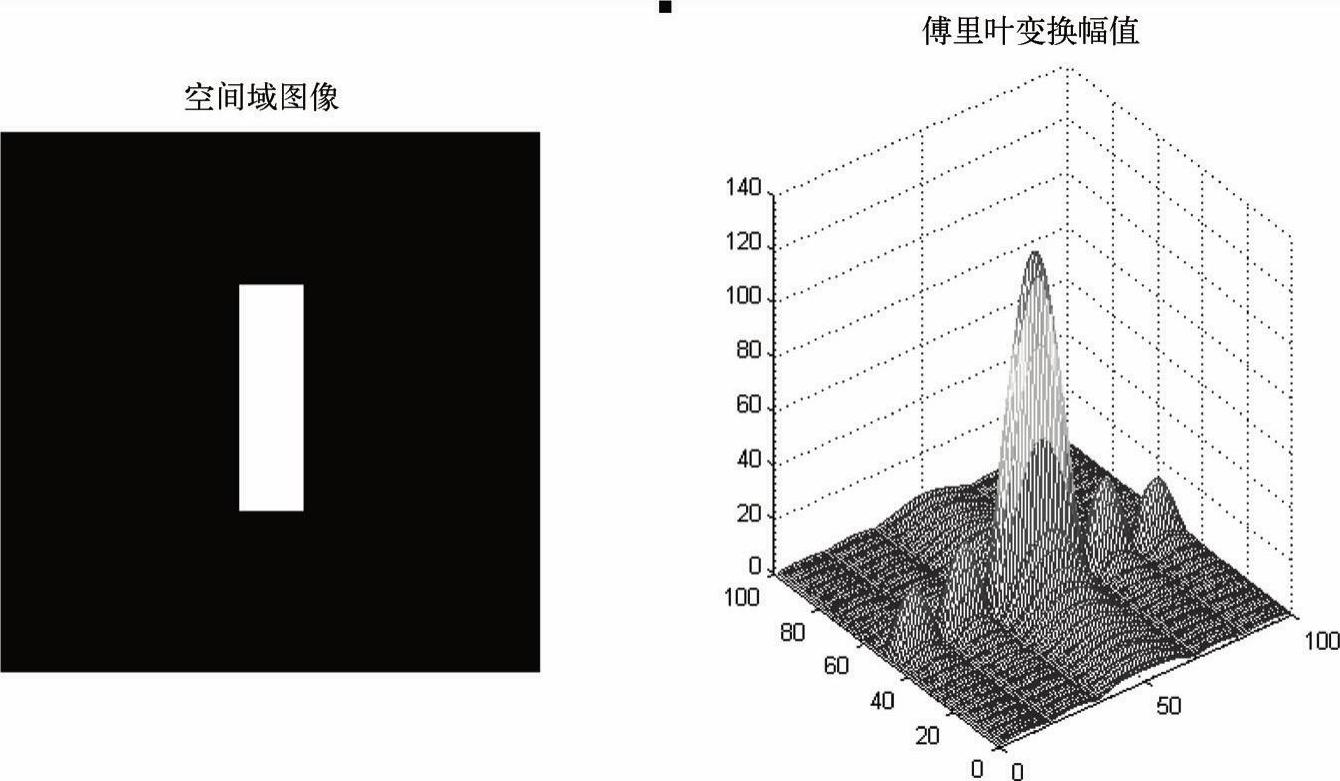
图2-16 矩形函数图像及其傅里叶变换幅值
(2)可分性
变换是可分的,即
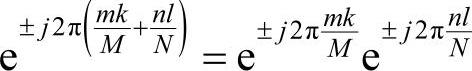
这个性质可使二维离散傅里叶变换依次用两次一维变换来实现。
(3)线性
离散傅里叶变换和反变换都是线性变换,即
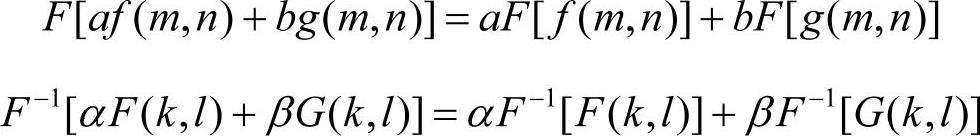
(4)尺度缩放性
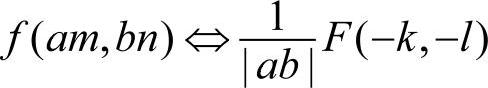
特别地,当a,b=-1时,有:
f(-m,-n)⇔F(-k,-l)
即离散傅里叶变换具有符号改变对应性。
(5)平移性质
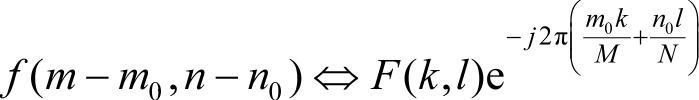
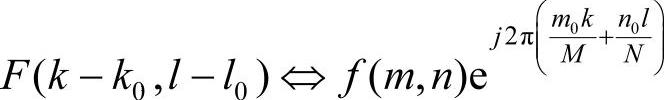
式中,m0,n0分别表示横纵方向的平移量。
对图像进行平移傅里叶变换和不平移傅里叶变换的效果如图2-17所示。

图2-17 对图像进行平移傅里叶变换和不平移傅里叶变换
a)原始图像 b)直接进行傅里叶变换 c)平移后进行的傅里叶变换
在阵列阵元有限的概念下,这种位移是循环位移。循环位移相当于原阵列周期延拓后的普通位移。这个性质表明,一个阵列发生平移,它的傅里叶变换阵列只改变相位,而幅值不变。
(6)旋转性质
在连续傅里叶变换中有
f(r,θ+θ0)⇔F(ρ,ϕ+ϕ0)
式中,θ0表示对应的旋转角大小。
将图像进行旋转后的傅里叶变换如图2-18所示。
 (https://www.xing528.com)
(https://www.xing528.com)
图2-18 将图像进行旋转后的傅里叶变换
(7)差分
令
Δxf(m,n)=f(m,n)-f(m-1,n)
Δyf(m,n)=f(m,n)-f(m,n-1)
则
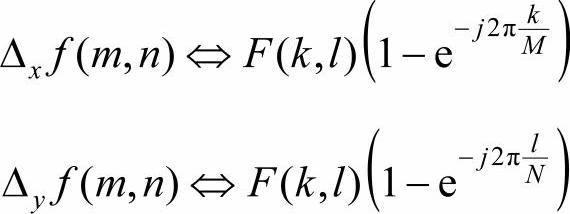
由该性质可知,在空间域中对图像进行差分运算相当于对图像进行高通滤波。
(8)和分
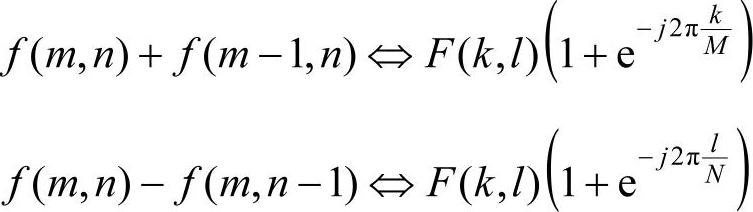
此性质表明,在空间域中对图像像素作和相当于对图像信号进行低通滤波。
(9)卷积
两幅图像的卷积等于其傅里叶变换的乘积,即
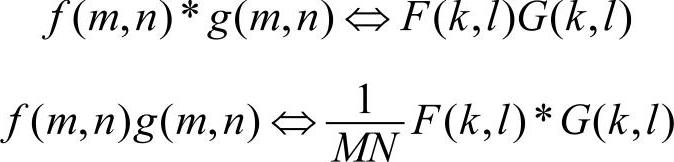
其中,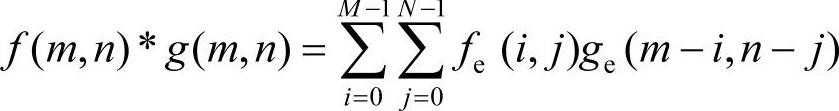 。
。
(10)图像的快速傅里叶变换
快速傅里叶变换(Fast Fourier Transform,FFT)的主要思想是将原函数分为奇数项和偶数项,通过不断将一个奇数项和一个偶数项相加(减),得到需要的结果。也就是说,FFT是将复杂的乘法运算变成两个数相加(减)的简单重复运算,即通过计算两个单点的DFT来计算一个双点的DFT;通过计算两个双点的DFT,来计算四个点的DFT…依此类推。
设离散函数f(m,n)在有限区域(0≤m≤M-1,0≤n≤N-1)非零,则快速傅里叶变换的主要推导过程如下。
令
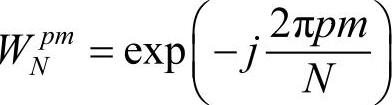
则有
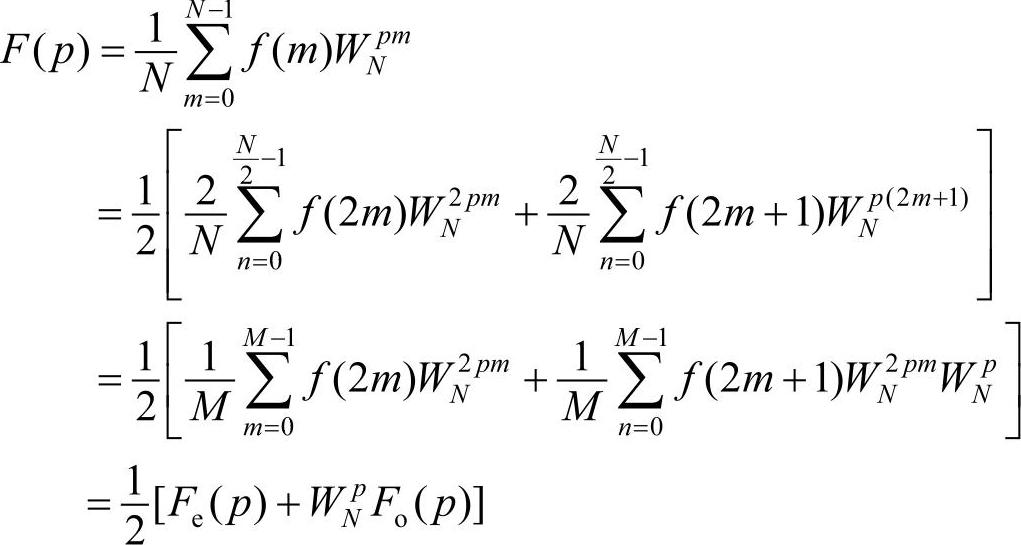
同理
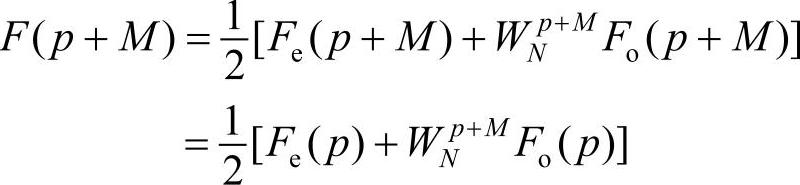
又因为
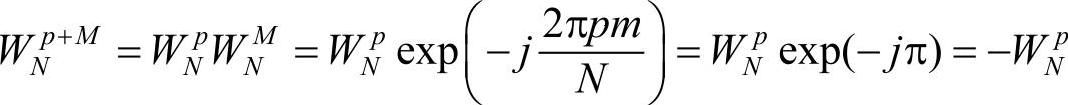
所以
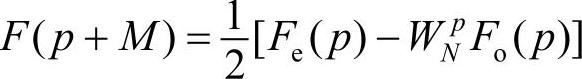
由上述推导,可得FFT的定义式为:
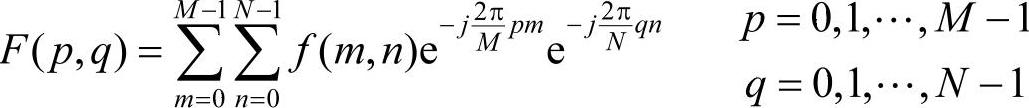
其逆变换为:
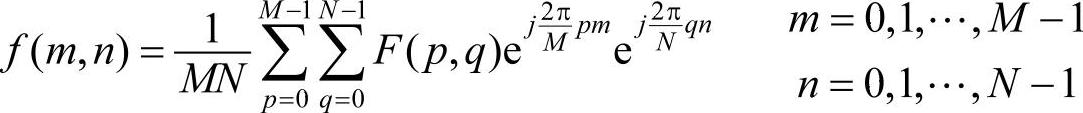
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




