在进行图像的比例缩放、旋转及复合变换时,原始图像的像素坐标(x,y)为整数,而变换后目标图像的位置坐标并非整数,反之亦然。因此,在进行图像的几何变换时,除了要进行几何变换运算之外,还需要进行灰度级插值处理。常用的灰度级插值方法有3种:最近邻插值法、双线性插值法和三次内插值法。
(1)最近邻插值法
最近邻插值法是一种简单的插值方法,如图2-8所示,它是通过计算与点P(x0,y0)邻近的四个点,并将与点P(x0,y0)最近的整数坐标点(x,y)的灰度值取为P(x0,y0)点灰度近似值。在P(x0,y0)点各相邻像素间灰度变化较小时,这种方法是一种简单快速的方法,但当P(x0,y0)点相邻像素间灰度值差异很大时,这种灰度估计值方法会产生较大的误差,甚至可能影响图像质量。
最邻近插值算法的MATLAB实现源程序如例程2-7所示,图2-9是例程2-7的运行结果。
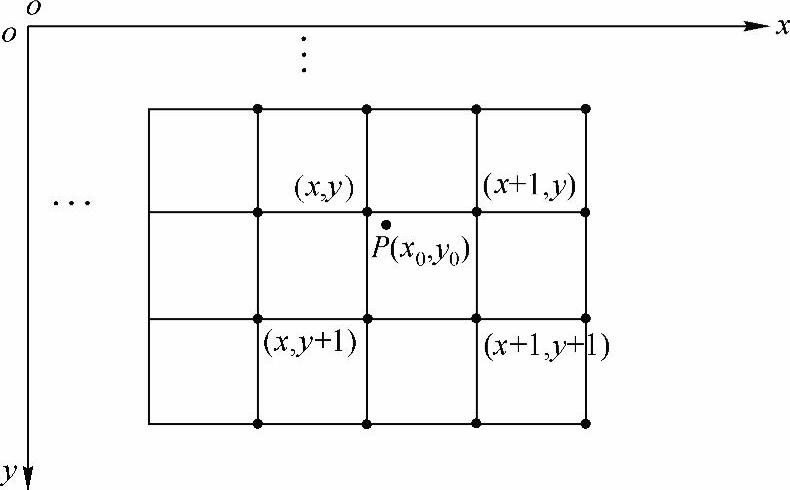
图2-8 最邻近插值法的示意图
例程2-7


图2-9 例程2-7的运行结果
a)输入的原始图像 b)最邻近插值后的图像
(2)双线性插值法
双线性插值法是对最邻近插值法的一种改进,即用线性内插方法,根据点P(x0,y0)的四个相邻点的灰度值,通过两次插值计算出灰度值f(x0,y0),如图2-10所示。
具体计算情况如下:
1)计算α和β
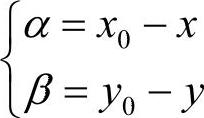
2)先根据f(x,y),f(x+1,y)插值求f(x0,y)
f(x0,y)=f(x,y)+α[f(x+1,y)-f(x,y)]
3)再根据f(x0,y+1),f(x+1,y)插值求f(x0,y+1)
f(x0,y+1)=f(x,y+1)+α[f(x+1,y+1)-f(x,y+1)]
4)最后根据f(x0,y)及f(x0,y+1)插值求f(x0,y0)
f(x0,y0)=f(x0,y)+β[f(x0,y+1)-f(x0,y)]=(1-α)(1-β)f(x,y)+α(1-β)f(x+1,y)+(1-α)βf(x,y+1)+βαf(x+1,y+1)=f(x,y)+α[f(x+1,y)-f(x,y)]+β[f(x,y+1)-f(x,y)]+βα[f(x+1,y+1)+f(x,y)-f(x,y+1)-f(x+1,y)]
式中,x=[x0];y=[y0]。
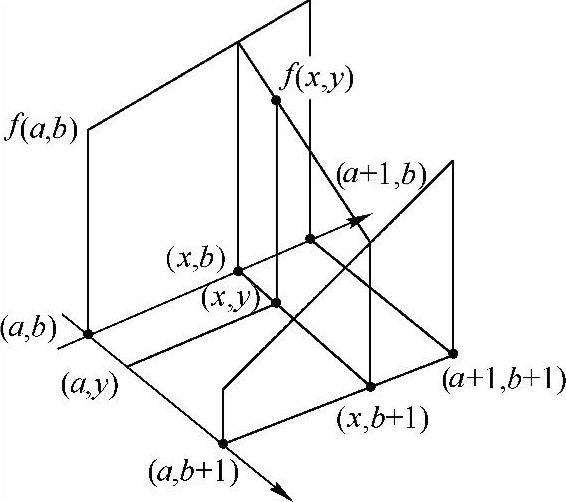
图2-10 双线性插值示意图
由于双线性插值法已经考虑了点P(x0,y0)的直接邻点对它的影响,因此一般可以得到令人满意的插值效果。但这种方法具有低通滤波性质(图像滤波将在本书2.4节介绍),高频分量会受到损失,使图像因细节退化而变得轮廓模糊。在某些应用中,双线性插值的斜率不连续还可能会产生一些不期望的效果。
例程2-8是运用双线性插值对图像进行放大的MATLAB源程序,其运行过程如图2-11a所示,运行结果如图2-11b所示。
例程2-8


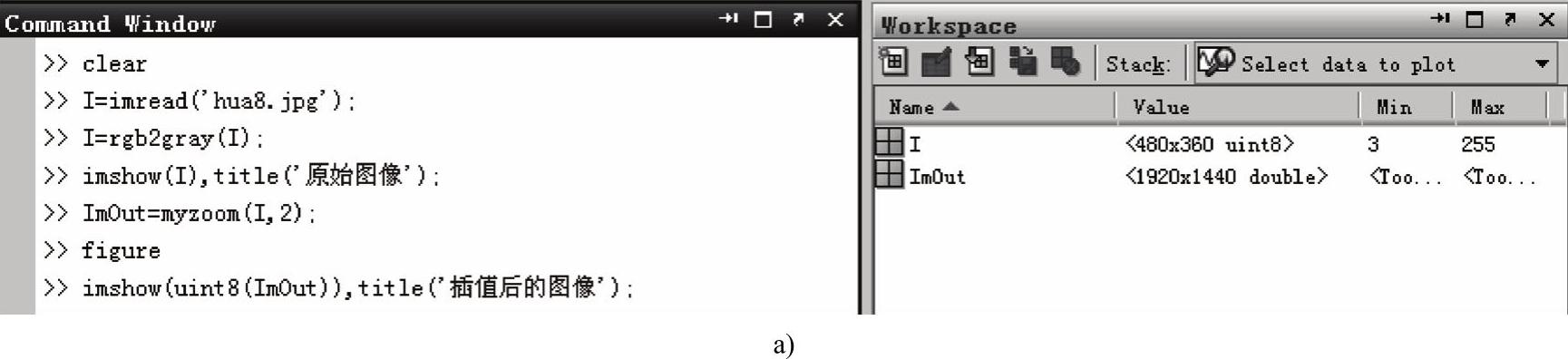
图2-11 运用双线性插值放大图像
a)例程2-8的运行过程(https://www.xing528.com)
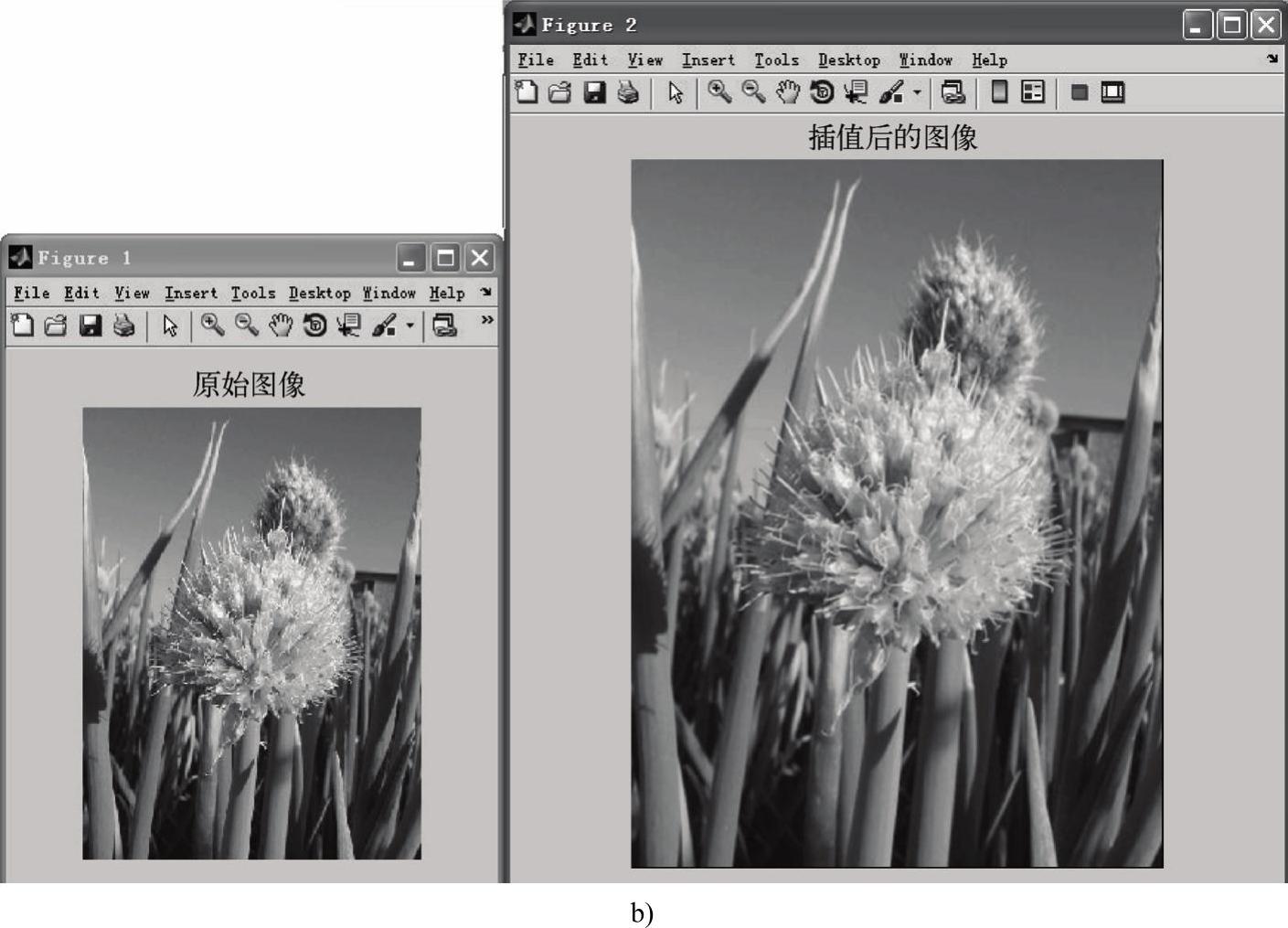
图2-11 运用双线性插值放大图像(续)
b)例程2-8的原始图像及其运行结果
(3)三次内插值法
为了得到更精确的P(x0,y0)点的灰度值,在更高程度上保证几何变换后的图像质量,实现更精确的灰度插值效果,可采用三次内插值法等更高阶插值法,如三次样条函数、Legendre中心函数和sin(πx)/(πx)函数等,这时既要考虑P(x0,y0)点的直接邻点对它的影响,还应考虑该点周围16个邻点的灰度值对它的影响(见图2-12)。
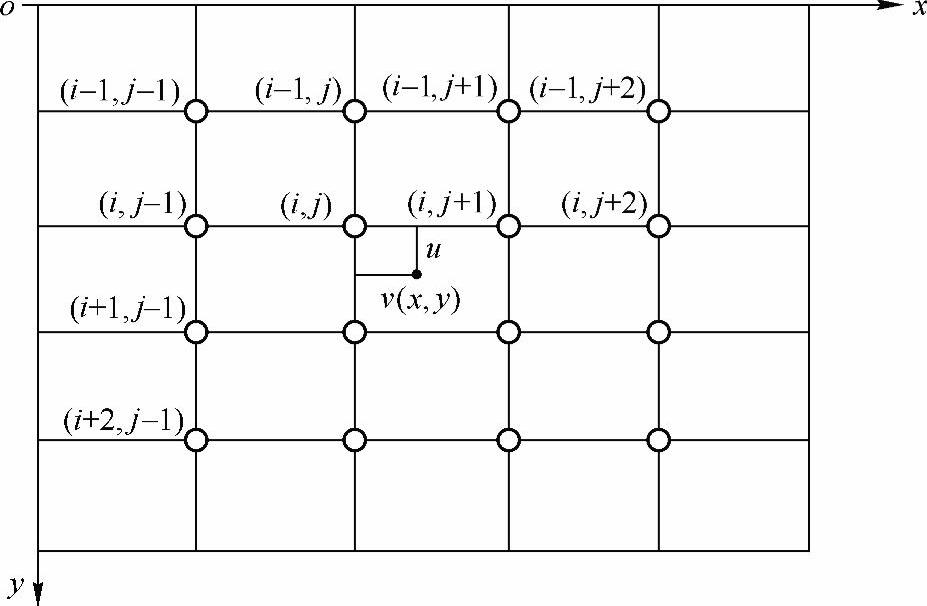
图2-12 三次内插值法的示意图
根据连续信号采样定理可知,若对采样值用插值函数s(x)=sin(πx)/(πx)进行插值,当采样频率不低于信号频谱最高频率的2倍时可以准确地恢复原信号,并可准确地得到采样点间任意点的值。
s(x)=sin(πx)/(πx)可以采用以下三次多项式近似。
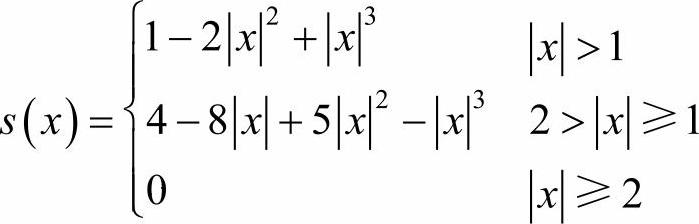
采用插值函数sin(πx)/(πx),可以按下述步骤差值算出f(x0,y0)。
1)计算s(1+α)、s(α)、s(1-α)、s(2-α)以及s(1+β)、s(β)、s(1-β)、s(2-β)。
2)根据f(x-1,y),f(x,y),f(x+1,y),f(x+2,y)计算f(x0,y)。
f(x0,y)=s(1+α)f(x-1,y)+s(α)f(x,y)+s(1-α)f(x+1,y)+s(2-α)f(x+2,y)
3)按步骤2)求f(x0,y-1),f(x0,y+1),f(x0,y+2)。
4)根据f(x0,y-1),f(x0,y),f(x0,y+1),f(x0,y+2)计算f(x0,y0)。
f(x0,y0)=s(1+β)f(x0,y-1)+s(β)f(x0,y)+s(1-β)f(x0,y+1)+s(2-β)f(x0,y+2)
上式计算过程可用矩阵表示为
A=(s(1+α)s(α)s(1-α)s(2-α))
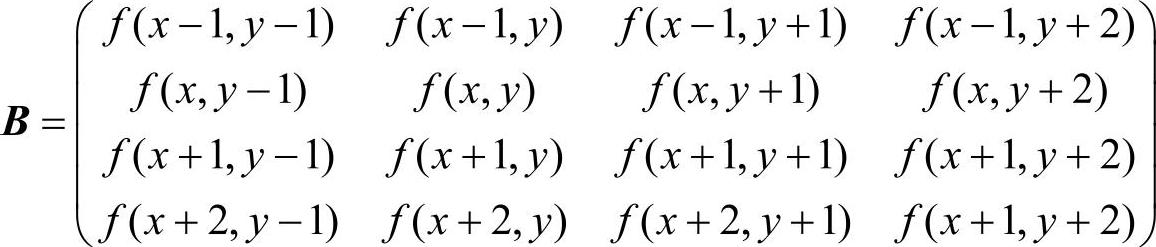
C=(s(1+β)s(β)s(1-β)s(2-β))T
在MATLAB数字图像处理工具箱提供了imresize函数,采用不同的插值方法可改变图像的大小,其调用格式如下。
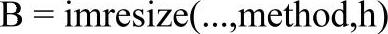
imresize函数使用由参数method指定的插值运算来改变图像的大小。method的几种可选值为:

例程2-9是调用imrersize函数进行图像放缩的MATLAB程序,其运行结果如图2-13所示。
例程2-9


图2-13例程2-9的运行效果
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




