图像几何变换的使用方法与技巧

（1）图像的平移变换

平移是日常生活中最普遍的方式之一，如开学时教室里课桌的重新摆放等都可以视为平移运动。图像的平移是将一幅图像上的所有像素点都按给定的偏移量沿x方向和y方向进行移动，如图2-1所示。图像的平移变换是图像几何变换中最简单的变换之一。

若对点A₀（x₀，y₀）进行平移后，被移动到A（x，y）的位置，其中，x方向上的平移量为Δx，y方向上的平移量为Δy，则点A（x，y）的坐标为：

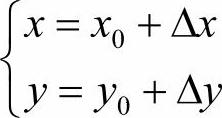
图2-1 图像平移示意图

利用齐次坐标，点A（x，y）的坐标可以表示如下。

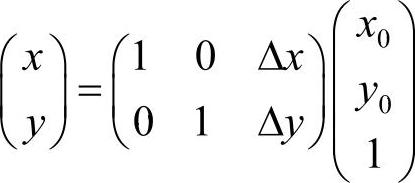
相应地，也可以根据点A（x，y）求解原始点A₀（x₀，y₀）的坐标，即

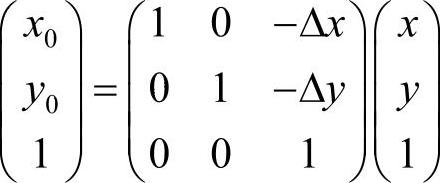
显然，以上两个变换矩阵互为逆矩阵。

图像平移变换的特点是平移后的图像与原图像完全相同，平移后新图像上的每一点都可以在原图像中找到对应的点。对于不在原始图像中的点，可以直接按它们的像素值统一设置为0或255，对于灰度图像则为黑色或白色。反之，若某像素点不在新图像中，同样说明原始图像中有某些像素点被移出了显示区域。图像经平移后，原始图像的一些像素点被移出了显示区域，若想保留全部图像，则应扩大新图像的显示区域。

例程2-1是图像平移的MATLAB程序，其运行过程如图2-2a所示，其运行结果如图2-2b所示.

例程2-1

图2-2 图像平移的MATLAB程序

a）平移的运行过程 b）平移的运行结果

(2)图像比例变换

通常情况下，数字图像的比例缩放是指给定的图像在x方向和y方向按相同的比例缩放a倍，从而获得一幅新的图像，又称为全比例缩放。如果x方向和y方向缩放的比例不同，则图像的比例缩放会改变原始图像像素间的相对位置，产生几何畸变。假设原始图像中的点A₀(x₀，y₀)比例缩放后，在新图像中的对应点为A₁(x₁，y₁)，则A₀(x₀，y₀)和A₁(x₁，y₁)之间的坐标关系可表示为

即

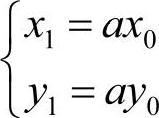
若比例缩放所产生的图像中的像素在原始图像中没有相对应的像素点时，就需要进行灰度值的插值运算，一般有以下两种插值处理方法。

1）直接赋值为和它最相近的像素灰度值，这种方法称为最邻近插值法（Nearest Neighbor Interpolation），该方法的主要特点是简单、计算量很小，但可能会产生马赛克现象。

2）通过其他数学插值算法来计算相应的像素点的灰度值，这类方法处理效果好，但运算量会有所增加。

有关灰度插值的内容，将在本节的2.1.2小节进行详细介绍。

在式（2-1）所表示的比例缩放中，若a＞1，则图像被放大；若a＜1，则图像被缩小。以a=1/2为例，即图像缩小为原始图像的1/2。图像被缩小1/2以后根据目标图像和原始图像像素之间的关系，有如下两种缩小方法。

第1种方法是取原始图像的偶数行和偶数列组成新的图像，缩放前后图像间像素点的对应关系如下。

以此类推，可以逐点计算缩小后图像各像素点的值，图像缩小之后所承载的信息量为原始图像的25%，即在原始图像上，按行优先的原则，对所处理的行，每隔一个像素取一点，每隔一行进行一次操作。另一种方法是取原始图像的奇数行和奇数列组成新的图像。

如果图像按任意比例缩小，则以类似的方式按比例选择行和列上的像素点。若x方向与y方向缩放的比例不同，则这种变换将会使缩放以后的图像产生几何畸变。图像x方向与y方向的不同比例缩放的变换公式如下。

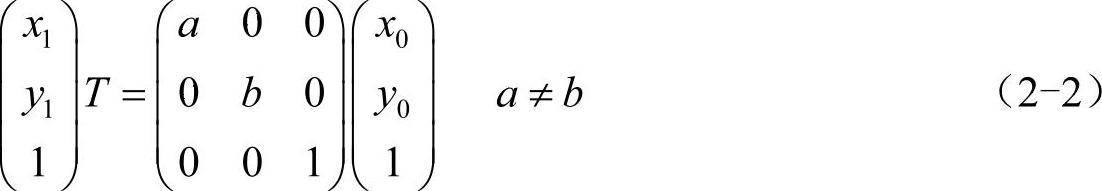
图像缩小变换是在已知图像信息中以某种方式选择需要保留的信息。反之，图像的放大变换则需要对图像尺寸经放大后所多出来的像素点填入适当的像素值，这些像素点在原始图像中没有直接对应点，需要以某种方式进行估计。以a=b=2为例，即原始图像按全局比例放大2倍，实际上，这是将原始图像每行中各像素点重复取一遍值，然后每行重复一次。根据理论计算，放大以后图像中的像素点（0，0）对应于原始图像中的像素点（0，0），（0，2）对应于原始图像中的像素点（0，1），但放大后图像的像素点（0，1）对应于原始图像中的像素点（0，0.5），（1，0）对应于原始图像中的（0.5，0），原始图像中不存在这些像素点，那么放大后的图像如何处理这些问题呢？以像素点（0，0.5）为例，这时可以采用以下两种方法和原始图像对应，其余点依此类推。

1）将原始图像中的像素点（0，0.5）近似为原始图像的像素点（0，0）。

2）将原始图像中的像素点（0，0.5）近似为原始图像的像素点（0，1）。

若采用第1种方法，则原始图像和放大图像的像素点对应关系如下。

若采用第2种方法，则原始图像和放大图像的像素点对应关系如下。

一般情况下，按比例将原始图像放大a倍时，如果按照最近邻域法，则需要将一个像素值添到新图像的a×a的方块中。因此，如果放大倍数过大，则按照这种方法填充灰度值会出现马赛克效应。为了避免马赛克效应，提高几何变换后的图像质量，可以采用不同复杂程度的线性插值法填充放大后所多出来的相关像素点的灰度值。

例程2-2

例程2-2实现的功能是将图像进行图像缩小或放大的MATLAB源程序，其运行过程如图2-3a所示，原始图像如图2-3b所示，缩小后的图像及其运行结果如图2-3c所示。

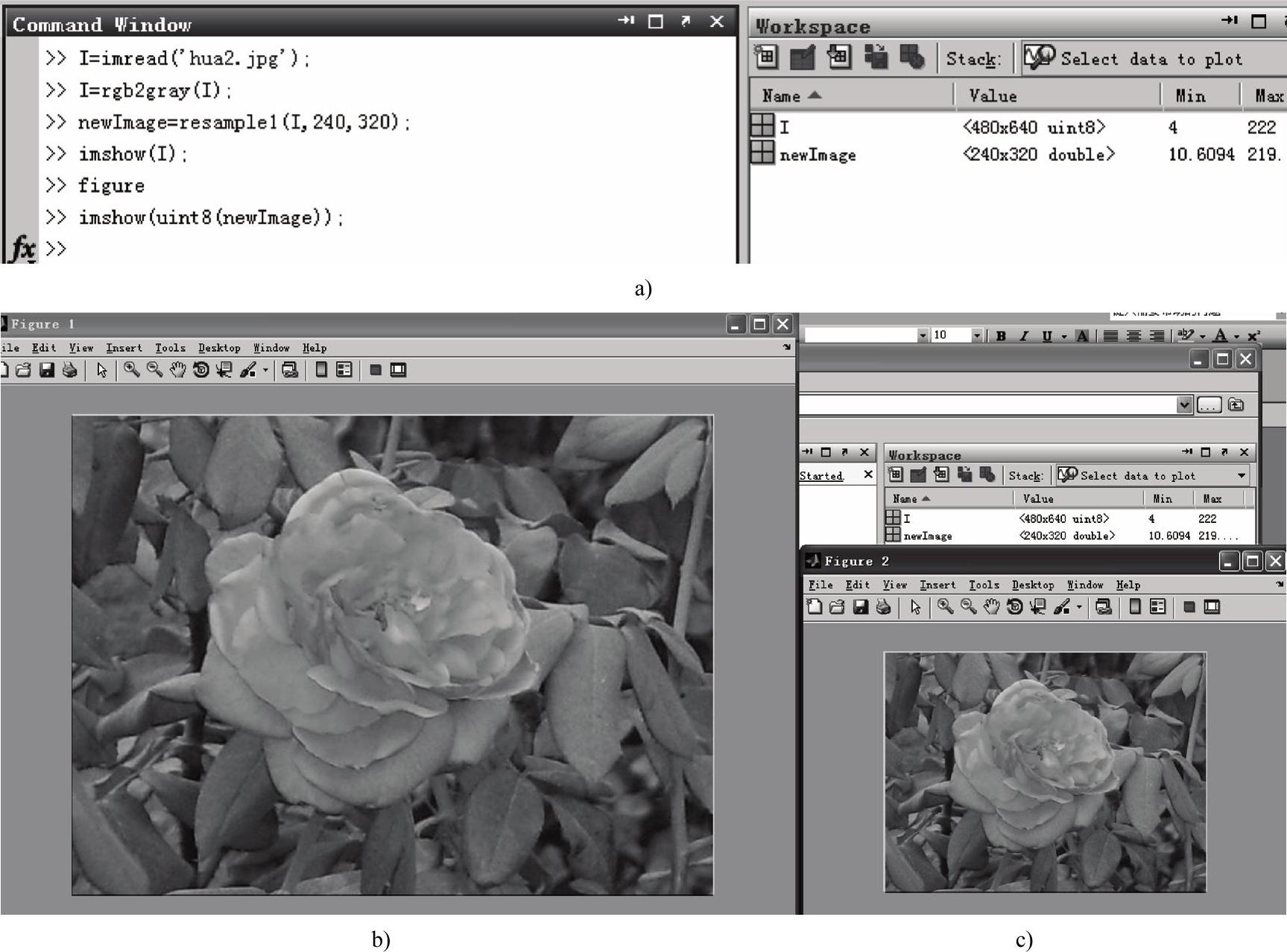
图2-3 缩小或放大的MATLAB源程序

a）例程2-2的运行情况 b）输入的原始图像 c）缩小后的图像和运行结果

在MATLAB中，图像的缩放也可以调用imresize函数来实现。imresize函数的调用格式如下。

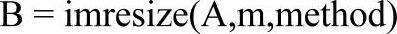
imrersize函数使用由参数method指定的插值运算来改变图像的大小。method的几种可选值为：′nearest′（默认值）最近邻插值；′bilinear′双线性插值；′bicubic′双三次插值；B=imresize(A，m)表示把图像A放大m倍。

例程2-3

例程2-3是调用imresize函数进行图像缩放的MATLAB程序，其运行结果如图2-4所示。

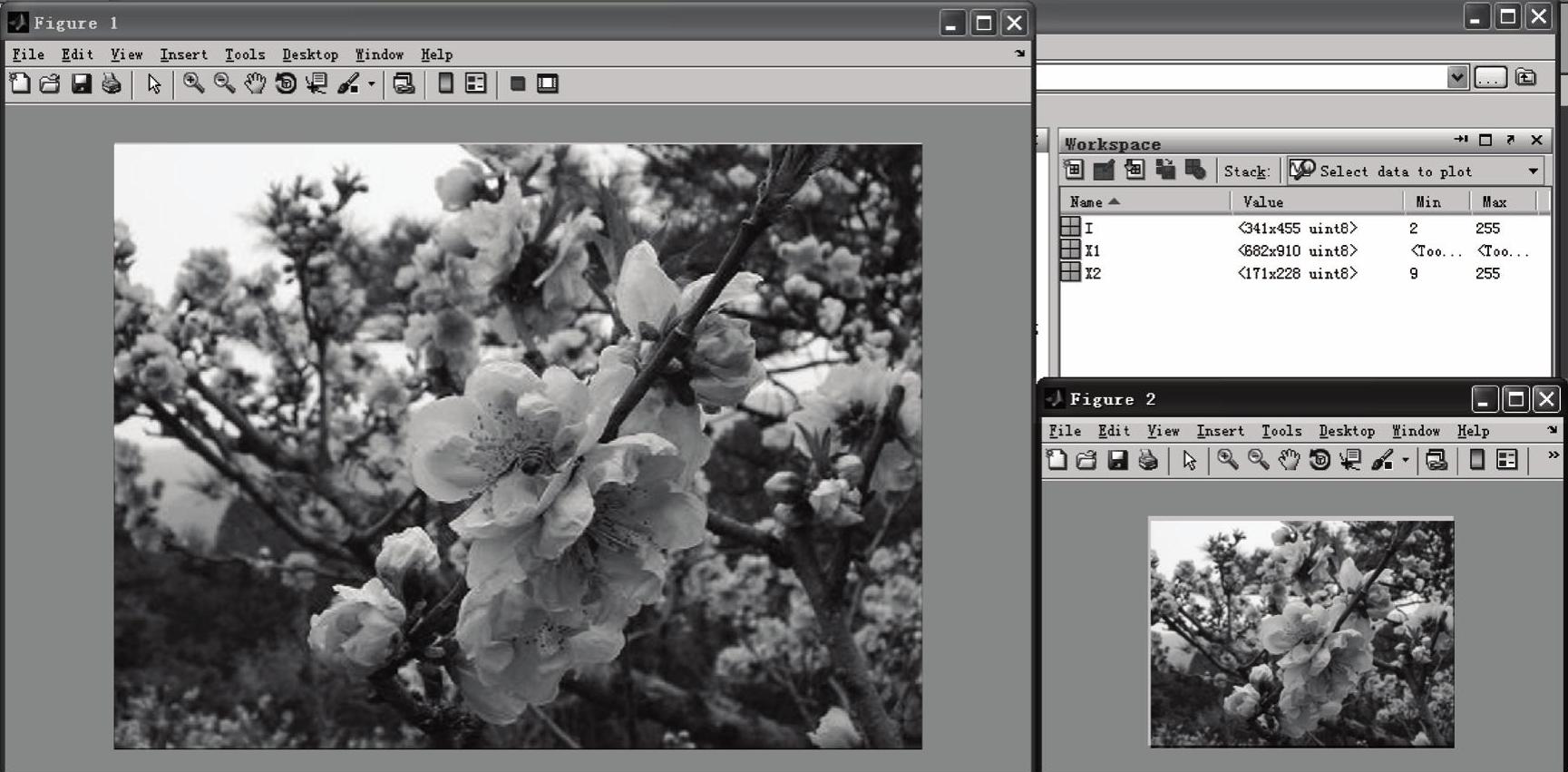
图2-4 例程2-3的运行结果

（3）图像旋转变换

提到旋转，首先要解决“绕着什么转”的问题。通常的做法是，以图像的中心为圆心旋转，将图像上所有像素都旋转一个相同的角度。图像的旋转变换是图像的位置变换，但旋转后图像的大小一般会改变。和图像平移变换一样，在图像旋转变换中，可以把转出显示区域的图像截去，旋转后也可以扩大图像范围以显示所有的图像。

采用不裁掉转出、部分旋转后图像放大的做法，首先需要给出变换矩阵。在坐标系中，将一个点顺时针旋转a角，r为该点到原点的距离，b为r与x轴之间的夹角。在旋转过程中，r保持不变。(www.xing528.com)

设旋转前x₀，y₀的坐标分别为x₀=rcosb，y₀=rsinb。当旋转a角度后，坐标x₁，y₁的值分别为

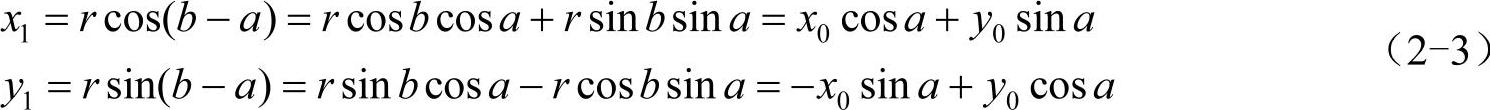
以矩阵的形式表示为

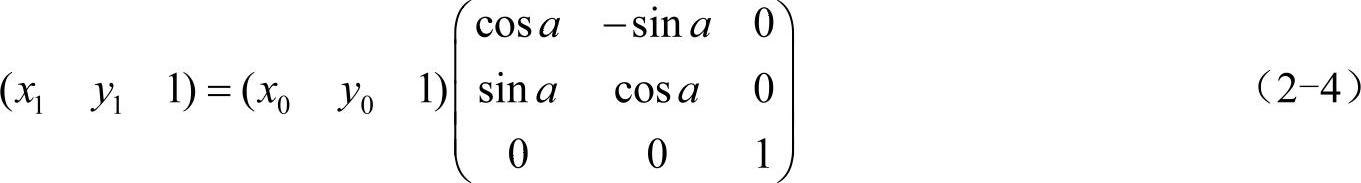
在式（2-4）中，坐标系xOy是以图像的中心为原点，以右为x轴正方向，以上为y轴正方向。

设图像的宽度为w，高度为h，容易得到

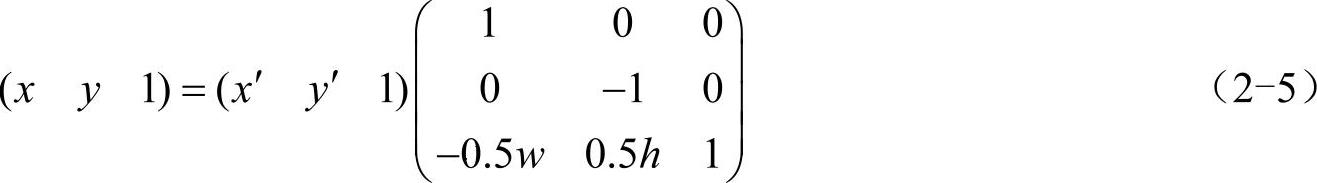
逆变换为

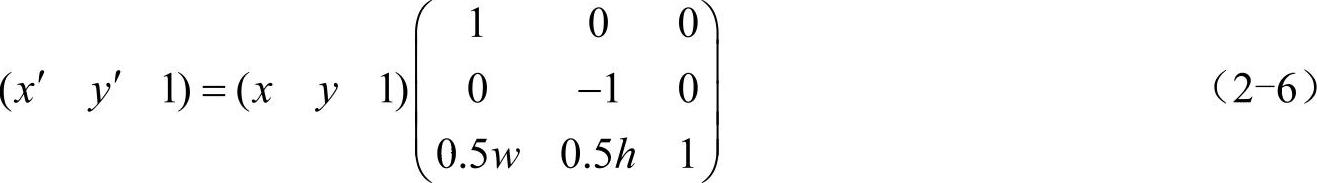
有了式（2-3）～式（2-6），可以将旋转变换分成3个步骤来完成：

1）将坐标系x′O′y′变成xOy。

2）将该点顺时针旋转a角。

3）将坐标系xOy变回x′O′y′，这样，就得到了如下的变换矩阵（是上面3个矩阵的级联）：

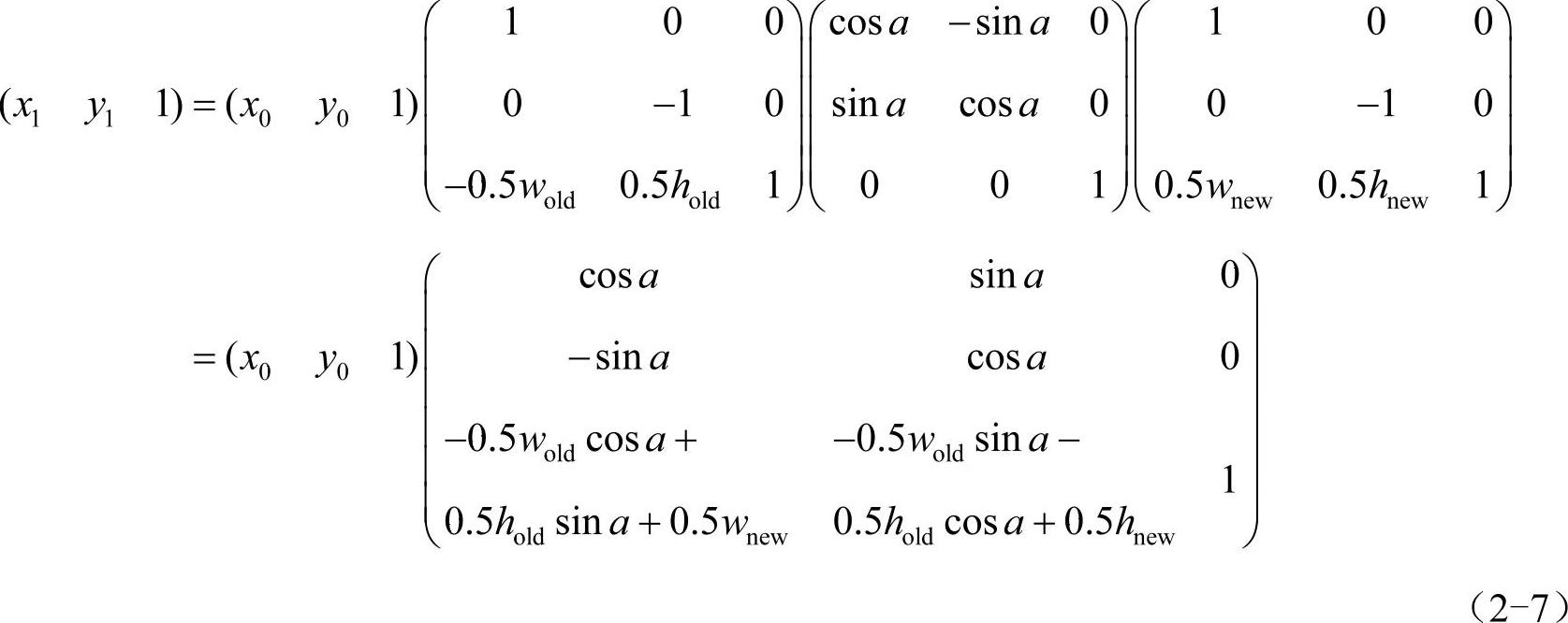
式中，w_old，h_old，w_new，h_new分别表示原图像的宽、高和新图像的宽、高。式（2-7）的逆变换为

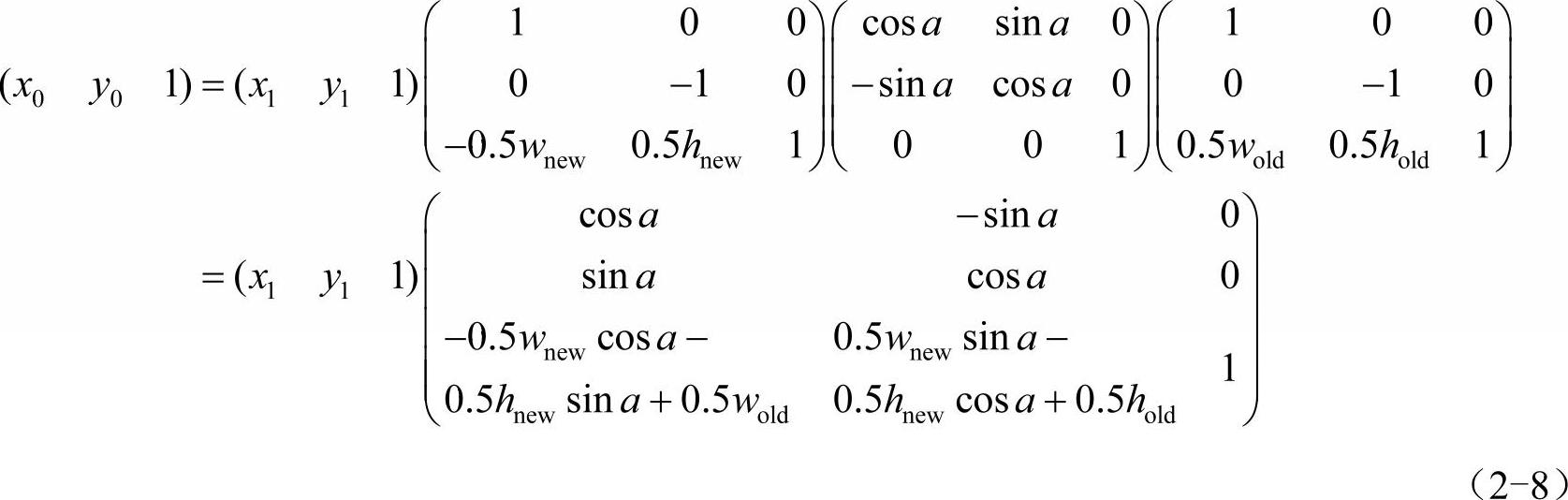
这样，对于新图像中的每一点，就可以根据式（2-8）求出对应点原图像中的点，并得到它的灰度。如果超出原图像范围，则填成白色。要注意的是，由于有浮点运算，计算出来的点坐标可能不是整数，需要采用取整处理，即找到最接近的点，这样会带来一些误差（图像可能会出现锯齿）。更精确的方法是采用插值，这将在2.1.2小节中进行介绍。

例程2-4是将图像进行旋转的MATLAB源程序，其运行过程如图2-5a所示，其输入的原始图像如图2-5b所示，其运行结果如图2-5c所示。

例程2-4

在MATLAB中，图像的旋转也可以通过直接调用imrotate函数来实现，其调用格式为：

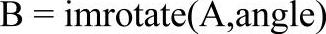
上述函数以图像中心点为基准，以角度angle逆时针方向旋转。指定angle为负值，可实现图像顺时针旋转。

例程2-5是调用imrotate函数进行图像放缩的MATLAB程序，其运行结果如图2-6所示。

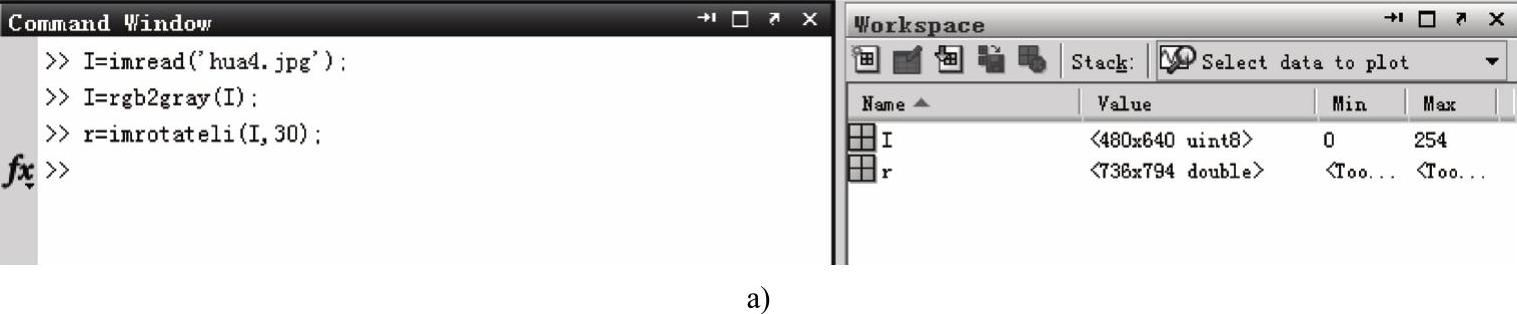
图2-5 对图像进行旋转

a）例程2-4的运行情况

图2-5 对图像进行旋转（续）

b）输入的原始图像 c）例程2-4的运行结果及其旋转后的图像

例程2-5

图2-6 例程2-5的运行结果

4）图像镜像变换

图像的镜像（Mirror）变换不改变图像的形状。图像的镜像变换分为3种：水平镜像、垂直镜像和对角镜像。

设图像的水平镜像操作是将图像左半部分和右半部分以图像垂直中轴线为中心进行镜像对换。设图像的大小为M×N，水平镜像可按式（2-9）计算：

式中，（i，j）为原图像F（i，j）中像素点的坐标；（i′，j′）为对应像素点（i，j）水平镜像变换后图像H（i′，j′）中的坐标。设原始图像的矩阵为

经过水平镜像的图像，行的排列顺序保持不变，将原来的列排列j=1，2，3，4，5转换成j'=5，4，3，2，1，即

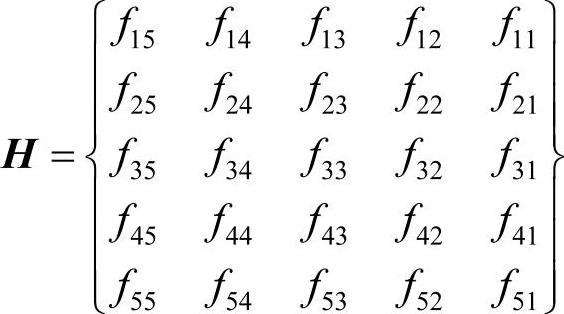
图像的垂直镜像操作是将图像上半部分和下半部分以图像水平中轴线为中心进行镜像对换。设图像的大小为M×N，垂直镜像可按式（2-11）计算：

式中，（i，j）为原图像F（i，j）中像素点的坐标；（i′，j′）为对应像素点（i，j）垂直镜像变换后图像H（i′，j′）中的坐标。

设原始图像的矩阵如式（2-10）所示，经过垂直镜像的图像，列的排列顺序保持不变，将原来行的排列i=1，2，3，4，5转换成i'=5，4，3，2，1，即

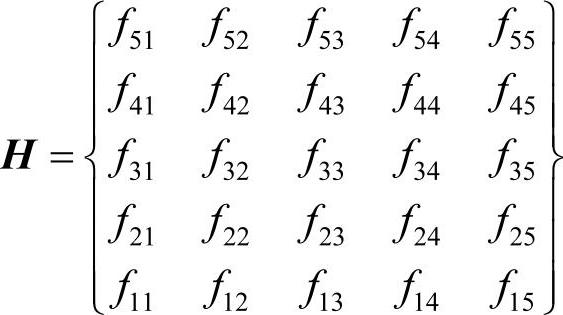
图像的对角镜像操作是将图像以图像水平中轴线和垂直中轴线的交点为中心进行镜像对换。相当于先水平镜像、后垂直镜像。设图像的大小为M×N，对角镜像可按式（2-12）计算：

式中，（i，j）为原图像F（i，j）中像素点的坐标；（i′，j′）为对应像素点（i，j）对角镜像变换后图像H（i′，j′）中的坐标。设原图像的矩阵如式（2-10）所示，经过对角镜像的图像，将原来的行排列i=l，2，3，4，5转换成i′=5，4，3，2，1，将原来的列排列j=l，2，3，4，5转换成，j′=5，4，3，2，1，即

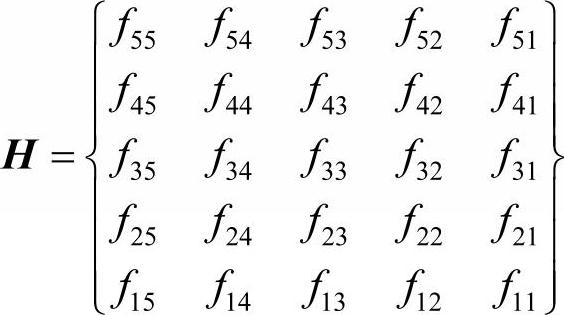
例程2-6是进行图像镜像变换的MATALB源程序，其运行过程如图2-7a所示，运行结果如图2-7b所示。

例程2-6

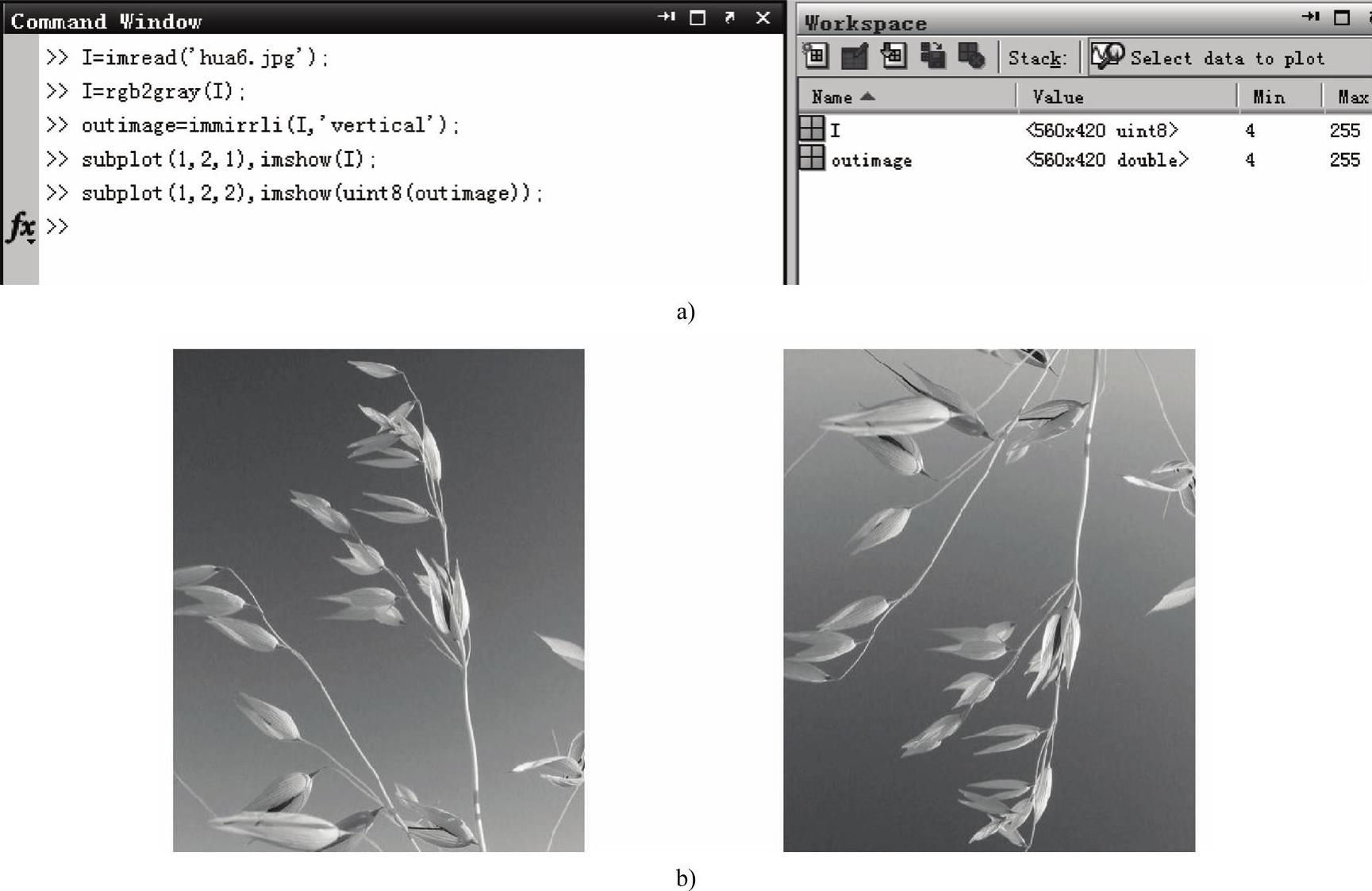
图2-7 图像镜像变换

a）例程2-6的运行情况 b）例程2-6的运行结果