如何检测网点增大值ZD？

检测网点增大值的方法有多种，比较精确的有以下三种：

（1）Δ值法

使用带刻度的高倍放大镜（刻度为0.001～0.01mm），观察晒制在印版上和印刷在承印物上对应的网点大小。则对于圆网点有：

式中　　Δ——圆形网点半径方向的增量，cm；

R1——晒制在印版上的某圆形网点的半径，cm；

R2——印刷在承印物上的该圆形网点的半径，cm。

正方形网点则有：

式中　　Δ——正方形网点边长上的单向增量，cm；

B1——晒制在印版上的某正方形网点的边长，cm；

B2——印刷在承印物上的该正方形网点的边长，cm。

在承印物、油墨、墨层厚度、水墨平衡、印刷压力等印刷条件都不变的前提下，对于不同网点面积覆盖率、不同网点点形和不同网线线数（线/厘米）的网点来说，Δ是一个常数。

在恒定的Δ值条件下，可计算出常用的网点点形（如圆形的和正方形的等），不同网线线数和不同面积覆盖率的网点增大值ZD，通过对照比较，就会发现：

①在网线线数和网点点形相同的前提下，面积覆盖率为50%的正方形网点的增大值最大。

②在网点点形和网点面积覆盖率相同的条件下，网点线数越高，网点增大值也越大。

③在网点面积覆盖率和网线线数不变的条件下，圆形网点的增大值最小。

形成上述三个重要特点的根本原因是：在单位面积内（1cm2），网点边缘长度之和越大，网点增大值也越大，否则，反之。

（2）默瑞—戴维斯（Murry-Davis）公式法

例如，由彩色反射密度计测得：白纸的密度调零为DW=0.00，以消除纸张灰度和色偏的影响；某原色实地密度DV=1.60；标称面积覆盖率为FF=75%的网点密度值DR=0.90，则网点实际覆盖率FD由式（4-10）求得：

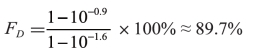
该处的网点增大值ZD为：

ZD=FD-FF=89.7 %-75 %=14.7 %

如果已知某色实地密度DV值以及该色网点面积覆盖率FD值，也可由式（4-10）的变换公式：

求得其网点密度值DR。

例如，已知DV=1.60，Dw=0.00，FD=70%，则该网点的密度值为：

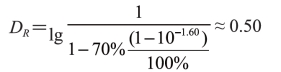
（3）尤尔—尼尔森（Yule-Nielsen）公式法

测算网点增大值的尤尔—尼尔森公式法与上述的默瑞—戴维斯公式法的区别，只是后者在测算ZD值时，是把机械性网点增大和光学性网点增大（简称光渗）合在一起所得的网点增大值，没有剔除光渗因素。尤尔—尼尔森公式则去除了光渗的影响，只考虑机械性网点增大的作用。故某处网点实际覆盖率为：

式中　　n——尤尔-尼尔森修正系数；

DV——某色实地密度；

DR——该色标称覆盖率为FF的网点主密度。

例如，用彩色反射密度计测得某青墨实地密度DV=1.60，在标称覆盖率为70%的青色网点测控块处的主密度DR=0.90，根据Murray-Davis公式法求得该处网点的实际覆盖率FD为：(www.xing528.com)

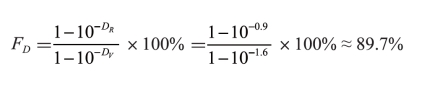
网点增大值为：

若采用式（4-12）即Yule-Nielsen公式法，已知尤拉—尼尔森修正系数n=1.5，则

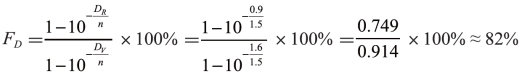
相应的网点增大值ZD为：

前者求得ZD=19.7%，实际是机械性网点增大与光渗（光学性网点增大）共同作用的结果；后者求得的ZD=12%，是剔除了光渗影响的几何面积覆盖率后的纯机械性的网点增大。

所谓光渗现象如图4-10所示，是由于入射光投射到印张上时，有一部分进入承印物内部，并在那里部分扩散，在印迹墨层下方的那部分光被吸收，从而造成反射密度DR的提高，所以在式（4-10）即默瑞—戴维斯公式所求得的ZD值，实质是两种网点增大的共同结果。

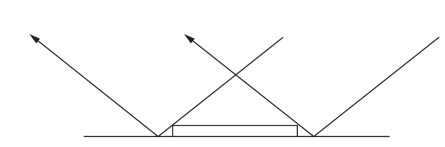
图4-10　光渗现象示意图

光渗作用的大小取决于承印物的光扩散程度、网线线数、网点形状、网点覆盖率以及彩色反射密度计的测量孔径等，为了使测试数据具有一定的可比性，必须使上述众多因素尽可能统一规定。

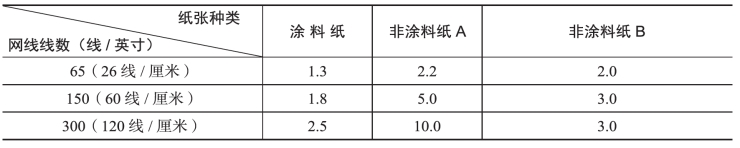
由此可见，Yule-Nielsen修正系数n是一个反映光渗程度大小的量。承印物的光扩散性能越好，网线线数越高，n值也就越大。n值的确定要根据承印物、网点大小、网点密度、网线线数、油墨和制版等条件的不同，反复试验确定，表4-4、表4-5和表4-6是国外有关资料上发表的n值范围，可供参考。当n=1时，式（4-12）成为它的特例式（4-10）。

表4-4　Yule-Nielson发表的n值的范围

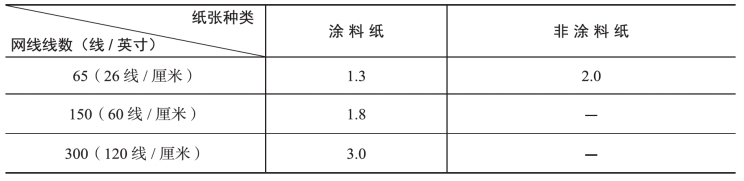
表4-5　及川善一郎发表的n值范围

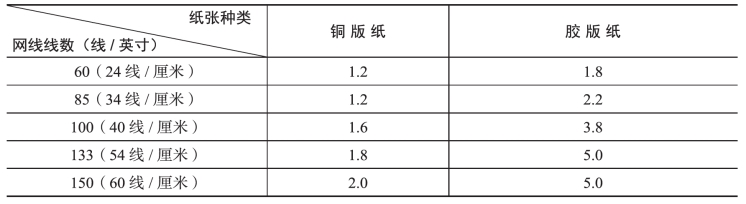
表4-6　美国B.E.Tory推荐的n取值范围

（4）Murray-Davis公式的推导

设：FD为单位面积内网点覆盖率；g是单位面积（1cm2）内网点面积所占的比例数；W为单位内空白部分所占的比例数。则有：

当g=0时，表明单位面积中均为空白部分，没有任何图文；g=1时，表明单位面积内全为图文部分，即实地。

当单位面积内有覆盖率为FD的网点时，此时的反射率ρR是两个乘积之和；即白纸的反射率ρW乘单位面积内空白部分所占比例数W与实地反射率ρV乘单位面积内网点所占比例数g之和，即：

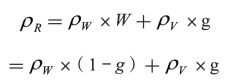
因为未经印刷的白纸用密度计测定时，要以其反射密度DW=0.00为校零基准，即ρW=1.00。则：

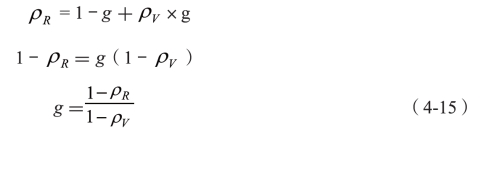
根据反射密度的定义可得：

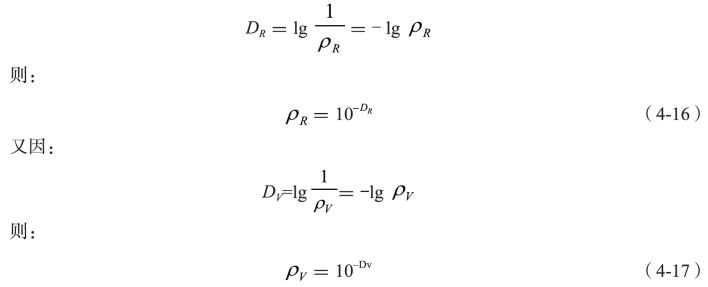
把式（4-16）和式（4-17）代入式（4-15）中得：

把式（4-18）代入式（4-13）中得：

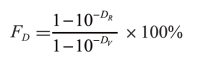
由此可见，Murray-Davis公式（4-10）是由实地反射密度DV和白场反射密度DW以及单位面积内网点所占比例数g的定义出发，推导而得的，其数学公式的物理意义是明确的。只是借助密度计测定网点密度时，不可避免地会把光渗因素包括进去，产生实测FD值大于理论计算值的情况。

如前所说，印刷产品首先是视觉商品，两种类型的网点增大（机械性网点增大和光渗，又称为网点的几何面积扩大和光学性网点增大）的综合结果，不仅不可避免地进入密度计的接收器，而且也不可避免地进入人们眼睛，引起视觉效果。因此Murray-Davis公式法测算网点增大值确有它的实用价值。