前馈补偿解耦控制：实现高效控制的方法

前馈补偿解耦控制是根据不变性原理来设计解耦控制器的，从而消除系统的相互关联。图8-15所示为双变量前馈补偿解耦控制系统。

图8-15 双变量前馈补偿解耦控制系统

要实现对U_c1与Y₂、U_c2与Y₁之间的解耦，根据前馈补偿原理可得

因此，前馈补偿解耦控制器的传递函数为

前馈补偿解耦后，图8-15所示的耦合系统将变为两个单回路控制系统。前馈补偿解耦与对角阵解耦具有相同的解耦效果，但前馈补偿解耦模型较简单，易于实现。另外，前馈补偿解耦还可以实现对扰动信号的解耦，前馈补偿解耦法是目前工业过程控制中应用最普遍的一种解耦方法。

例如已知双输入双输出耦合控制系统如图8-16所示。试设计解耦控制器。

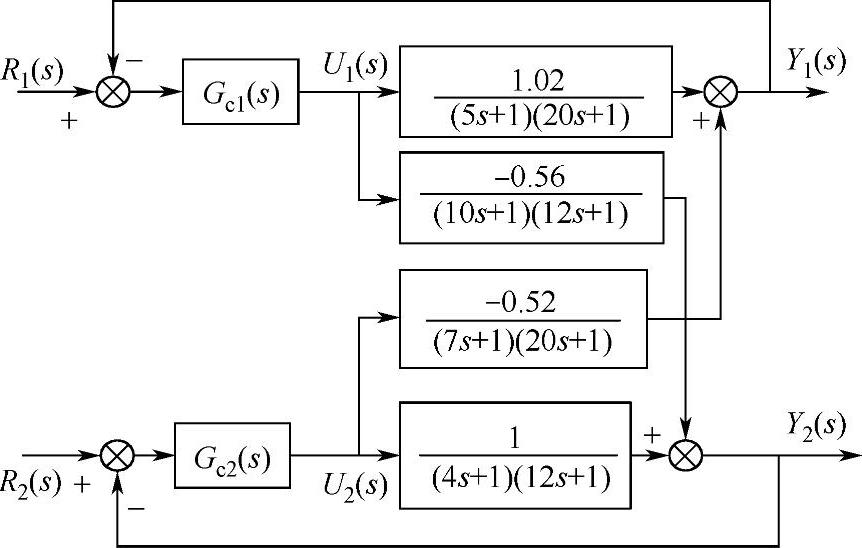
图8-16 双输出耦合控制系统

解：由图8-16可知，被控对象的传递函数矩阵为

(www.xing528.com)

首先对系统进行耦合分析：由被控对象的传递函数矩阵得系统静态放大系数矩阵为

K即为系统的第一增益系数矩阵。

系统相对增益矩阵为

由相对增益矩阵看到，系统通道之间存在严重耦合，且系统输入与输出的配对正确。系统采用前馈补偿解耦法进行解耦设计。

根据式（8-15），前馈补偿控制器为

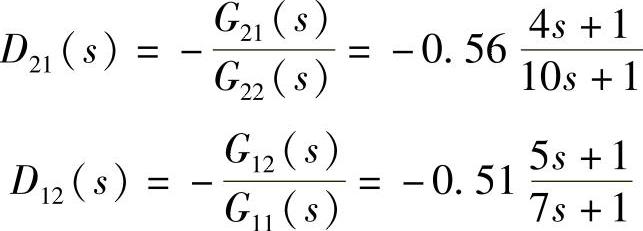
采用前馈补偿解耦后，系统变为两个独立的单输入单输出系统，为了保证系统无稳态误差，控制器采用PI控制，参数整定为K_P1＝6、T_I1＝50、K_P2＝4、T_I2＝37。为了说明前馈补偿解耦正确性，我们对无耦合系统、耦合系统和前馈补偿解耦系统仿真研究，图8-17所示为系统采用前馈补偿解耦的Simulink仿真框图。图8-18a所示依次为系统无干扰时第一通道对应单回路输出、前馈解耦输出、第二通道对应单回路输出、前馈解耦输出；图8-18b所示为系统施加0.2的随机干扰时的干扰信号、第一通道对应单回路输出、前馈解耦输出、第二通道对应单回路输出、前馈解耦输出。

从图上可以明显看到，采用前馈解耦不仅可以做到将耦合系统等效为单回路控制系统，同时前馈解耦系统的抗干扰能力、反应速度等也大大提高。