对角阵解耦控制优化方案

对角阵解耦控制是多变量解耦控制中最早使用的一种解耦方法。图8-5所示为对角阵解耦的双变量控制系统结构图。

对角阵解耦要求被控对象特性矩阵与解耦控制矩阵的乘积等于对角阵G∗（s），即

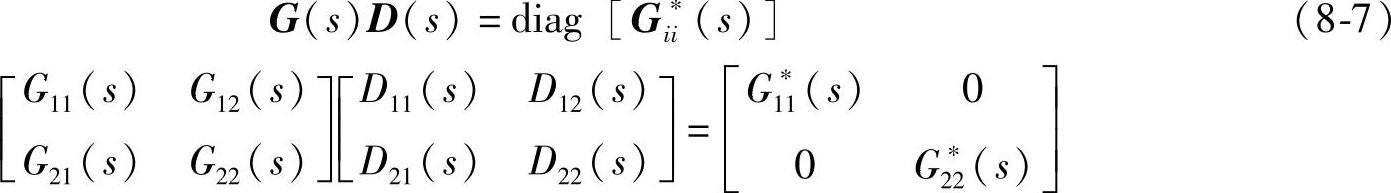
因此，被控对象的输出与输入变量之间满足如下矩阵方程：

通过对角阵解耦，多变量系统变为相对独立的单变量控制系统。

图8-5 双变量对角阵解耦系统结构图

假设被控对象传递函数矩阵G（s）为非奇异矩阵，则解耦控制器的数学模型由式（8-7）求得

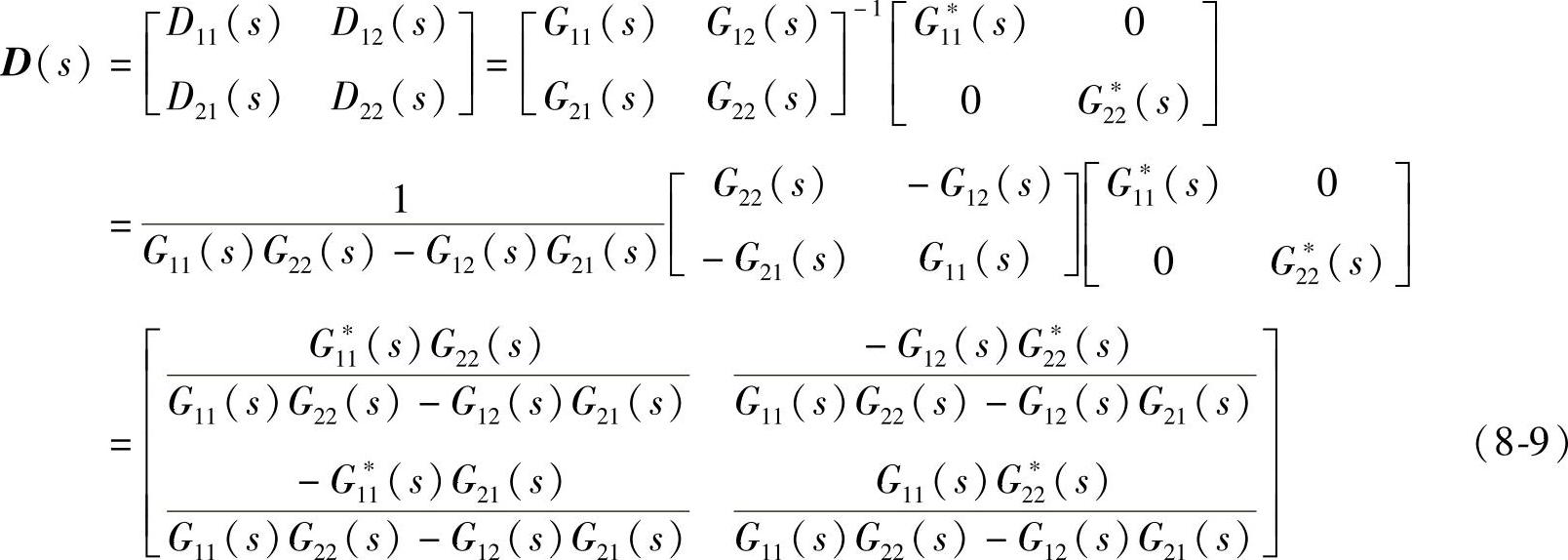
对角阵解耦后的等效控制系统如图8-6所示。

例如已知双输入双输出耦合系统如图8-7所示。

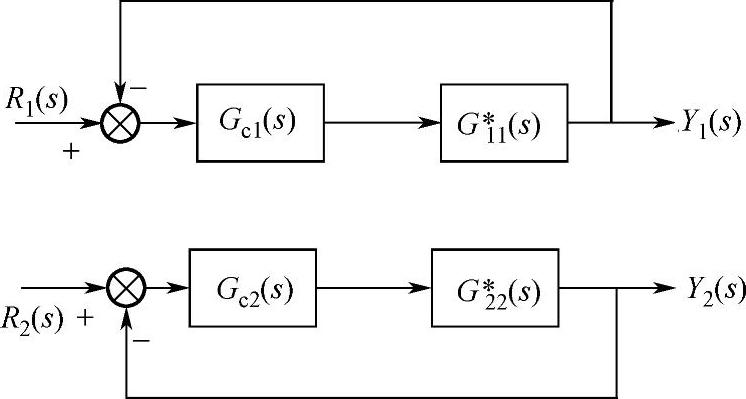
图8-6 对角阵解耦后的等效控制系统

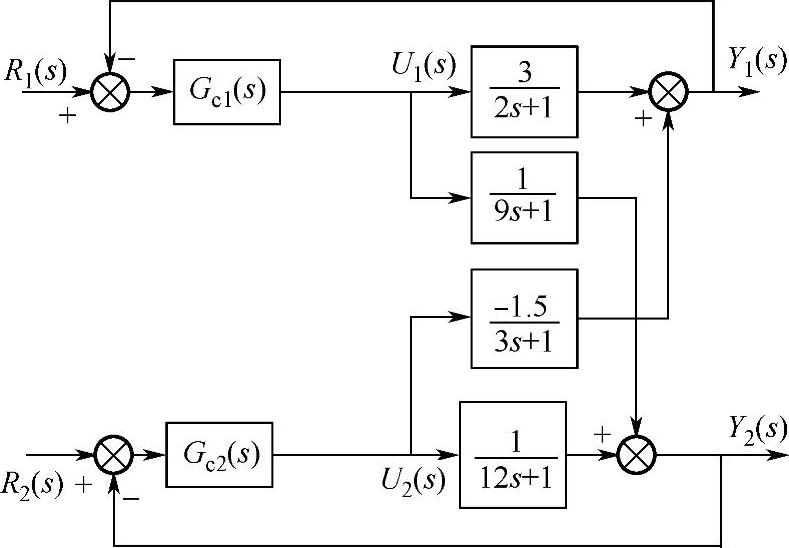
图8-7 双变量耦合控制系统

要求解耦后系统的传递函数矩阵为

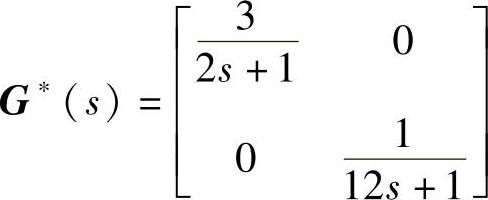
试设计解耦控制器。

解：由图8-7可知，被控对象的传递函数矩阵为

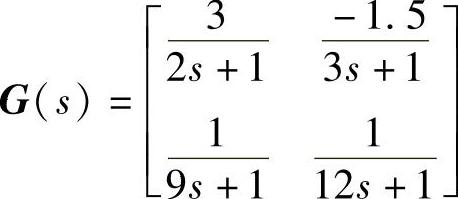
首先对系统进行耦合分析，由被控对象的传递函数矩阵得系统静态放大系数矩阵为

K即为系统的第一增益矩阵。

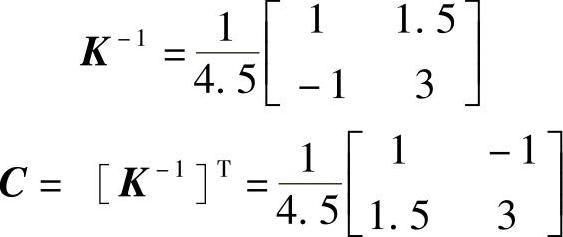
则系统相对增益矩阵为(www.xing528.com)

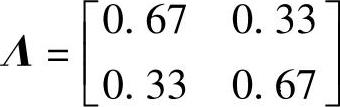
由相对增益矩阵可以看到，系统通道之间存在严重耦合，且系统输入与输出的配对正确。系统采用对角阵解耦法进行解耦。

根据式（8-9）可得解耦控制器的传递函数矩阵为

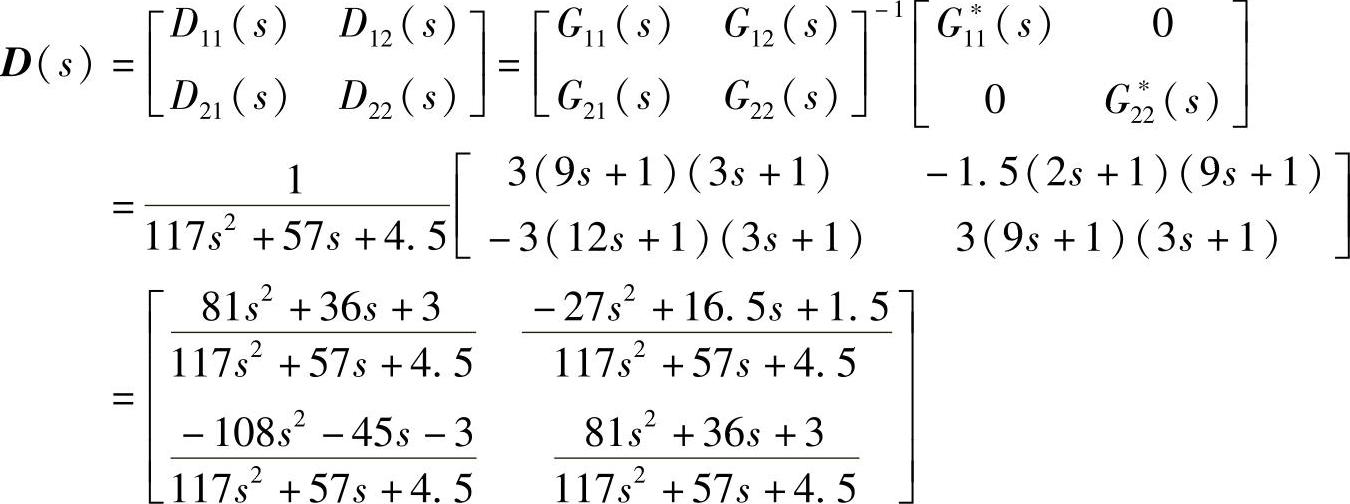
系统不存在耦合时的Simulink仿真框图如图8-8所示。

两个单输入单输出系统的控制器选择PI控制规律，参数整定为K_P1＝0.8、T_I1＝0.71、K_P2＝1、T_I2＝2.86，系统的单位阶跃响应如图8-9所示，依次为给定信号、第一通道的输出响应、第二通道的输出响应。

系统耦合的Simulink仿真框图如图8-10所示，对应系统阶跃响应曲线如图8-11所示。

从图8-9和图8-11来看，系统的耦合主要影响响应的幅值、响应速度、系统稳定性。

图8-8 不存在耦合时的Simulink仿真框图

图8-9 不存在耦合时的响应曲线

图8-10 存在耦合时的Simulink仿真框图

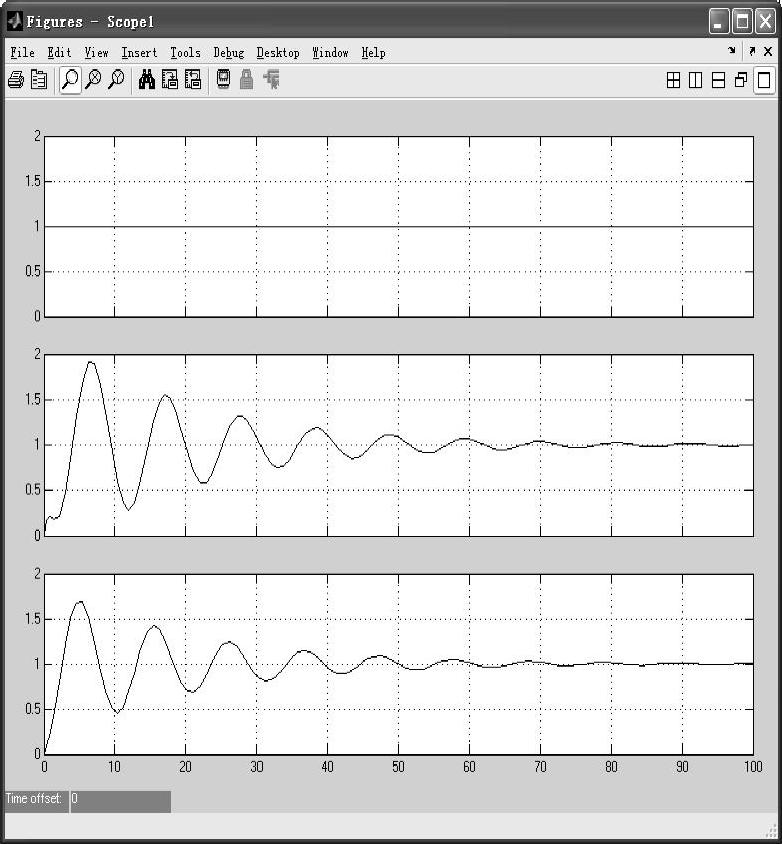
图8-11 存在耦合时的阶跃响应曲线

按前面对角阵设计的解耦控制器，系统单回路和解耦系统比较的Simulink仿真框图如图8-12a所示，系统在阶跃信号作用下响应曲线如图8-12b所示，依次为第一单回路系统输出响应、第一输出解耦后输出响应、第二单回路系统输出响应、第二输出解耦后输出响应。

解耦系统施加随机干扰的Simulink仿真框图如图8-13所示，系统在阶跃信号作用下，施加幅度为0.1的随机干扰的响应曲线如图8-14所示，依次为给定信号、随机干扰、输出响应Ⅰ和输出响应Ⅱ。

由图8-12和图8-14可以看到，对于耦合程度较严重的系统，在已知被控对象的精确数学模型的情况下，采用对角阵解耦可以变成独立的单变量系统，且控制器参数的整定可仿照单变量系统进行。

但是，必须指出，对于多变量耦合控制系统，经过对角阵解耦求出的解耦控制器的数学模型可能过于复杂，并且变量越多，解耦控制模型越复杂，实现解耦控制器就越困难。

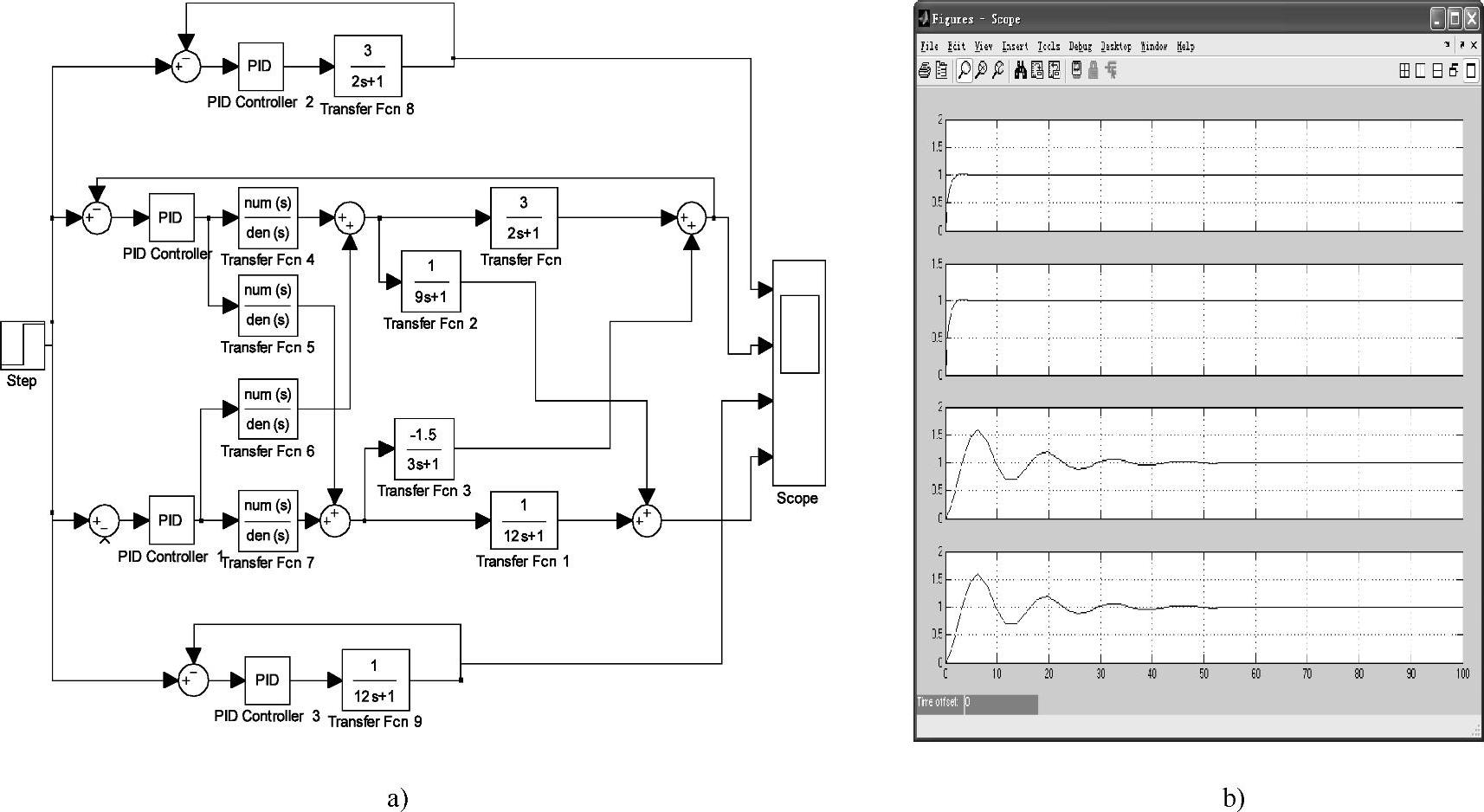
图8-12 单回路与对角阵解耦比较系统的Simulink仿真框图

图8-13 对角阵解耦系统整体Simulink仿真框图