多变量控制系统的耦合及优化方法

在线性控制系统中，经常假设系统只有一个被控变量。影响这个被控变量的诸多因素中，选择一个控制量，而其他因素均看成系统的扰动，构成单输入单输出控制系统。然而实际系统是复杂的，大多是多个过程参数需要控制，并且影响这些被控变量的控制量也往往不只一个，构成多输入多输出的过程控制系统。其中系统中常常一个输入将影响到多个输出，而一个输出也往往受到多个输入的影响，即系统各个输入输出变量之间的通道存在耦合。例如图8-1所示为流量、压力相互耦合的控制系统。

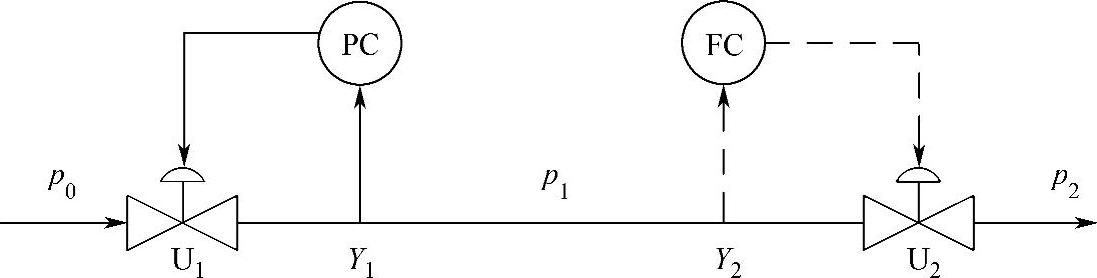
图8-1 流量、压力相互耦合的控制系统

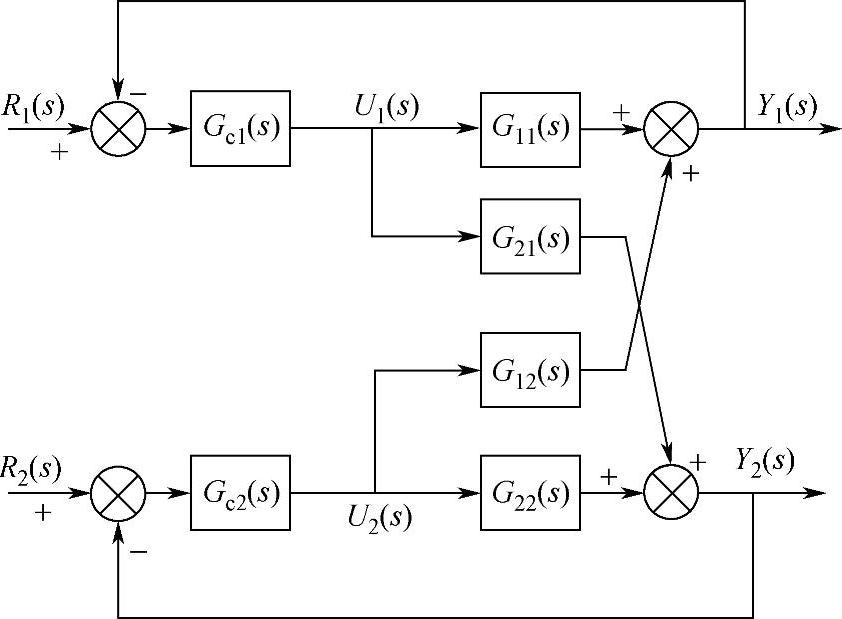
图8-2 双输入双输出控制系统结构框图

系统中流量和压力两个控制系统分别投入运行时，各个控制系统能正常运行。但是，如果两个控制系统同时运行时，控制阀U₁或U₂的开度变化不仅对各自的控制系统有影响，同时也对另一个控制系统有影响。例如，当压力Y₁低于要求值，则要求压力控制系统开大控制阀U₁，此时另一流量变量Y₂也随之增大，而流量控制系统又必须关小控制阀U₂，结果又使得压力升高。反之，流量控制阀的开度变化同样也会引起压力变化，从而使两个控制系统相互影响，这种影响称为系统的关联或耦合。控制系统之间的相互耦合将直接影响各被控变量和控制信号之间的独立控制作用，有时甚至会破坏各自系统的正常工作。

过程控制系统中变量之间的耦合（关联）是普遍存在的，各变量之间有时有强耦合（强关联），而有时只是松散的耦合，甚至无耦合。过程控制系统之间的耦合（关联）程度可用传递函数矩阵表示。图8-2所示为双输入双输出耦合控制系统结构框图。

从图8-2中可以看出，控制器G_c1（s）的输出U₁（s）不仅通过传递函数G₁₁（s）影响系统输出Y₁（s），而且还通过交叉通道传递函数G₂₁（s）影响系统的输出Y₂（s）；同样，控制器G_c2（s）的输出U₂（s）不仅通过传递函数G₂₂（s）影响系统输出Y₂（s），而且还通过交叉通道传递函数G₁₂（s）影响系统的输出Y₁（s）。

上述耦合关系可用传递函数矩阵来描述

Y（s）＝G（s）U（s） （8-1）(www.xing528.com)

或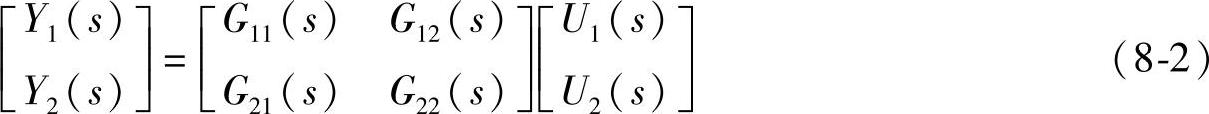

式中 Y（s）——输出矩阵；

U（s）——输入矩阵；

G（s）——传递函数矩阵。

确定各变量之间耦合程度的分析方法有直接法和相对增益法。直接法是采用解析法得到各变量之间的传递函数关系，从而确定过程中每个变量相对每个控制作用的耦合程度。相对增益法是一种通用的耦合特性分析工具，通过相对增益矩阵不仅可以确定变量之间的耦合程度，而且可依此去设计解耦控制系统。

相对增益矩阵是衡量多变量系统各变量之间耦合程度的静态参数。以图8-3所示静态时的双输入双输出系统为例说明几个定义，图8-3中，k₁₁、k₁₂、k₂₁和k₂₂为系统传递函数的静态增益系数。

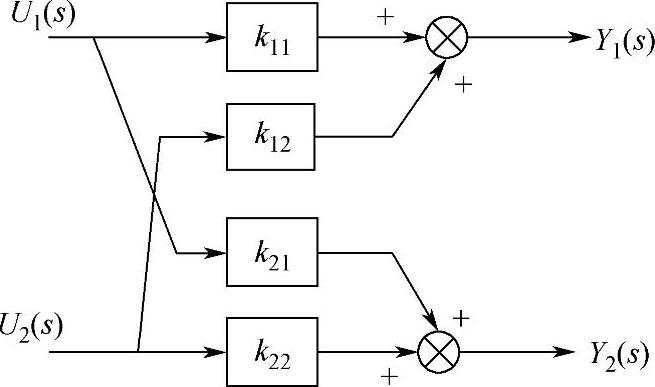
图8-3 双输入双输出对象的静态特性框图