预估补偿控制方法探究

当系统中有纯滞后环节（滞后时间比较大），会导致系统控制不及时，常规PID控制、微分先行控制、中间反馈控制往往难以取得显著效果。而预估补偿控制按照大纯滞后的工业过程的特性，设想一种模型（补偿器）加到反馈控制系统中，力图使控制滞后了τ的被控量提前反映到控制器上，使控制器提前动作，从而明显地减小或补偿了时滞给系统造成的不利影响，有效地降低了系统的超调量和过渡过程时间，提高了系统的控制质量。常见的预估补偿控制有Smith预估、Dahlin算法等。

1.Smith预估补偿原理

为了改善大时滞系统的控制品质，1957年史密斯（O.J.M.Smith）提出了以模型为基础的预估补偿控制方案。

对于如图7-41所示具有纯滞后的过程控制系统，控制器输出U（s）到系统输出Y（s）的传递函数为

控制器的输出要滞后时间τ才起作用。纯滞后时间τ愈大，系统滞后的愈严重，系统的稳定性大大降低，系统的控制品质下降。

Smith预估补偿是设想在广义的被控对象上并联一个补偿环节（补偿控制器）G_c∗（s），来达到消除纯时滞对系统的影响，Smith预估补偿控制原理的结构图如图7-42所示。

图7-41 常规控制系统结构图

图7-42 Smith预估补偿控制系统结构图

由图7-42可知，反馈信号Y∗（s）与系统控制信号之间U（s）的传递函数为

为了使控制器的输出信号与反馈信号之间无时延，即要求

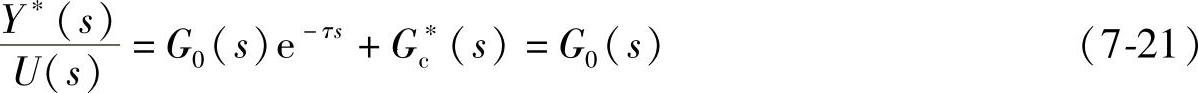
由式（7-21）可求得Smith预估补偿控制器的传递函数为

G_c∗（s）＝G₀（s）（1-e-τs） （7-22）

2.Smith预估补偿控制系统

在实际应用中，Smith预估补偿控制器并不接在被控对象上，而是反向并接在控制器上，如图7-43所示。

由图7-43得Smith预估补偿控制系统设定值、扰动信号作用下的闭环传递函数分别为

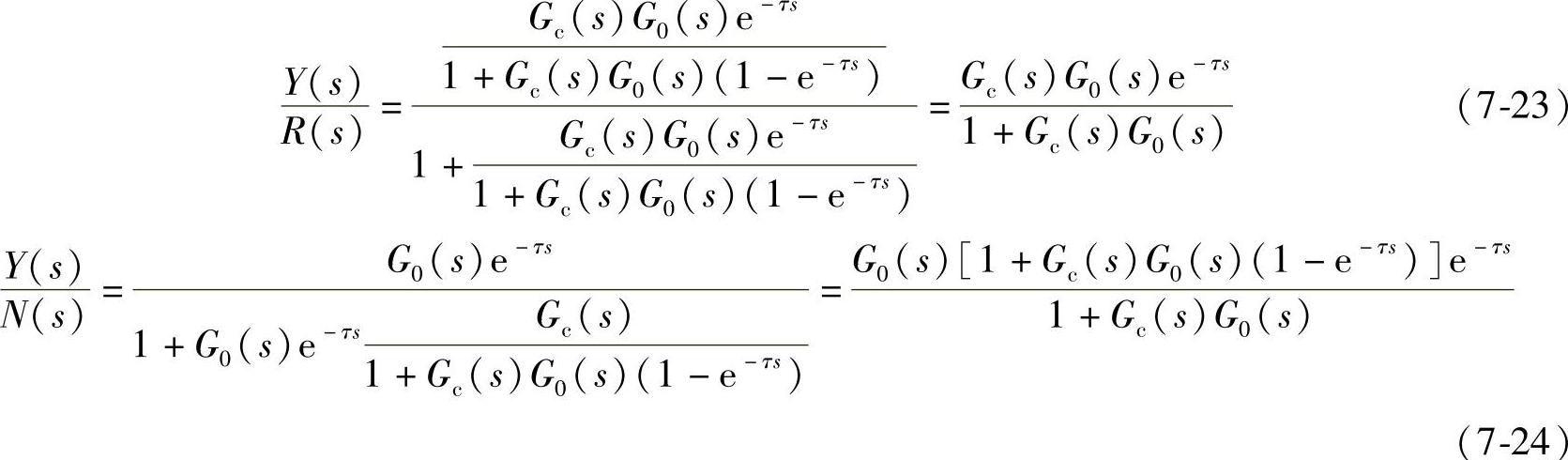
无论在设定值还是扰动信号作用下，闭环系统的特征方程式均为

D（s）＝1+G_c（s）G₀（s）＝0 （7-25）

从式（7-25）可见，系统的特征方程已不包含纯滞后环节，即系统已经消除了纯滞后对系统控制品质的影响。而闭环传递函数分子上的纯滞后e-τs仅仅将系统的被控量在时间上推迟了时间τ。

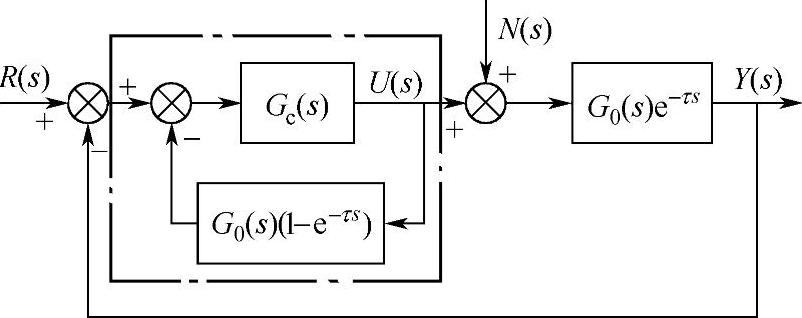
图7-43 Smith预估补偿控制系统

对于一阶惯性加纯滞后的被控对象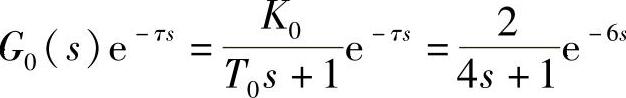，，采用常规PI控制器（K_P＝0.35，T_I＝125）时，设定值为5，常规PID控制和Smith预估补偿控制给定信号作用下的输出响应如图7-44所示。系统稳定运行下施加幅值为50％的干扰系统的输出响应曲线如图7-45所示。当被控对象的参数变化，而控制器参数不变，采用Smith预估补偿控制方案，被控对象增益变化时，系统的响应曲线如图7-46所示，被控对象时滞变化时系统的响应曲线如图7-47所示。

图7-44 给定信号作用下常规PID控制和Smith控制输出响应

图7-45 干扰信号作用下系统的输出响应曲线

图7-46 对象增益变化Smith预估补偿控制输出响应

从而可以看到，当被控对象模型精确已知时Smith预估补偿效果较好，但当被控对象发生变化（参数、时滞）时，Smith预估补偿效果欠佳。

3.Smith预估补偿控制的注意事项

从理论上分析，Smith预估补偿器可以完全消除时滞的影响，成为一种解决时滞系统的理想方案，但是在实际使用中却很不尽人意，主要原因有：

1）Smith预估补偿控制是基于过程模型已知的情况下的，因此Smith预估补偿前提是必须精确地已知被控过程的数学模型，即过程传递函数和时滞时间。由式（7-22）知Smith预估补偿控制的效果完全取决于补偿控制器模型的精度。

2）对于大多数过程控制系统，过程模型不可能与实际生产过程的特性完全一样，并且实际过程的特性还要随操作条件的变化而变化。要使过程模型越接近实际过程的特性，过程模型必定很复杂，导致补偿器的结构很复杂，难于在工业生产中广泛应用。

图7-47 对象时滞变化Smith预估补偿控制输出响应

为此，仍以上面的过程控制系统为例，如果被控过程的时滞τ与预估控制器的时滞τ^∗相差较大时，假设系统在幅值为5的阶跃信号和幅度为0.5的随机干扰作用下的响应曲线如图7-48所示，依次为模型精确匹配、τ与τ^∗相差为2时的响应曲线；图7-49所示依次为模型精确匹配、K₀与K₀^∗相差为4时的响应曲线。从图中明显地可以看出Smith预估补偿控制方案对模型的误差十分敏感。尤其当K₀和τ的变化较大时，Smith预估补偿就失去了良好的控制效果。(www.xing528.com)

图7-48 模型参数增益失配时Smith预估补偿的响应曲线

如何改善Smith预估补偿器的各种方法悠然而生，如增益自适应补偿控制器、完全抗干扰的Smith预估器等。

4.增益自适应补偿控制

增益自适应补偿控制是1997年由贾尔斯（R.F.Giles）和巴特利（T.M.Bartley）提出的，它在Smith预估补偿控制系统的基础上增加了一个除法器、一个比例微分和一个乘法器，其结构如图7-50所示。

增益自适应补偿控制中的除法器将过程的输出值除以模型的输出值；比例微分环节中的T_D＝τ，它将过程输出比估计模型输出提前τ的时间送入乘法器；乘法器是将预估器输出乘以比例微分环节的输出送入到控制器。这三个环节的作用是要根据模型和过程信号之间的比值提供一个自动校正预估器的增益信号。

在理想情况下，预估器模型与过程模型精确的一致时，除法器输出为1，此时增益自适应补偿控制蜕化为Smith预估补偿控制，过程的纯时延环节已被有效地排除在闭环控制回路之外，控制系统的等效框图如图7-51所示。

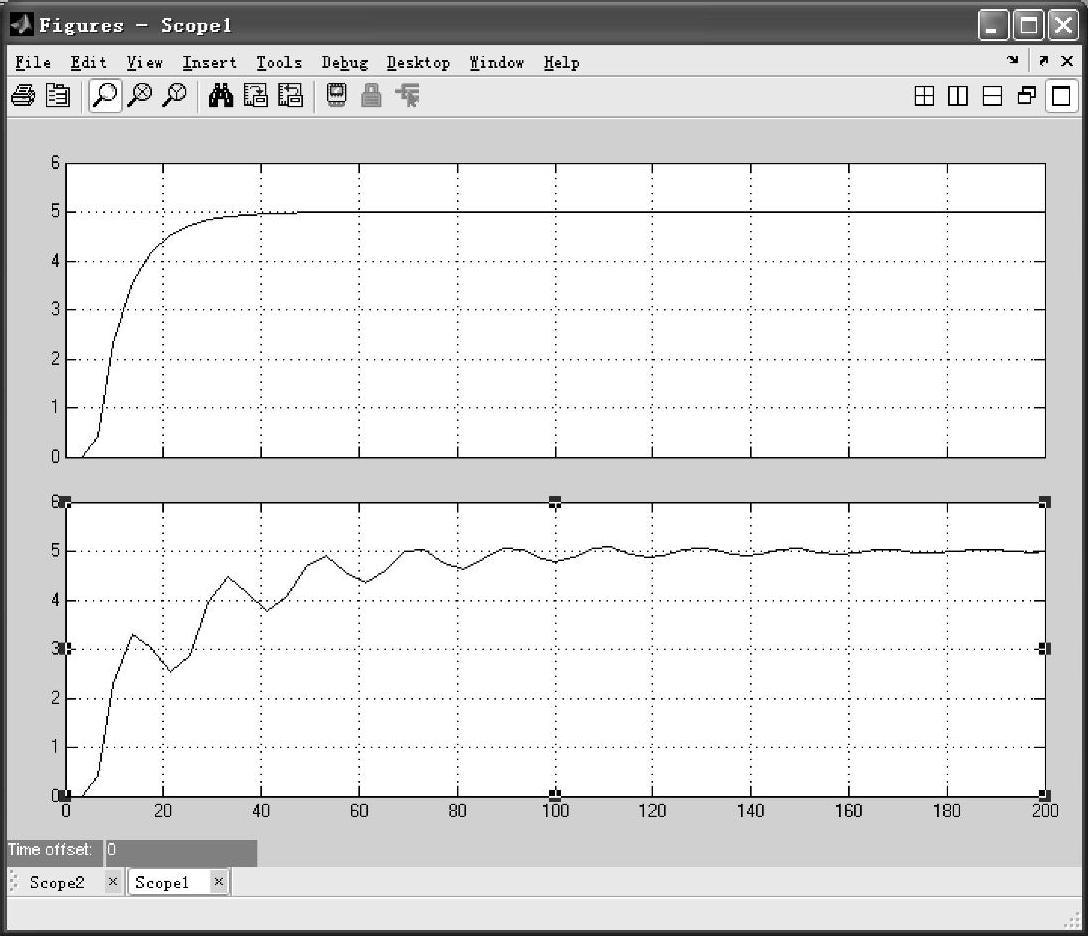
图7-49 模型参数时滞失配时Smith预估补偿的响应曲线

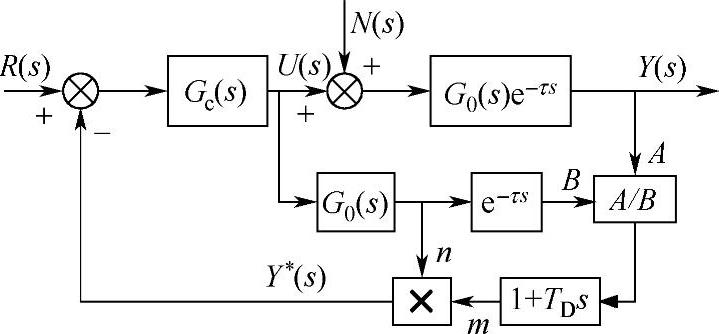
图7-50 增益自适应补偿控制结构图

图7-51 理想条件下增益自适应补偿系统等效框图

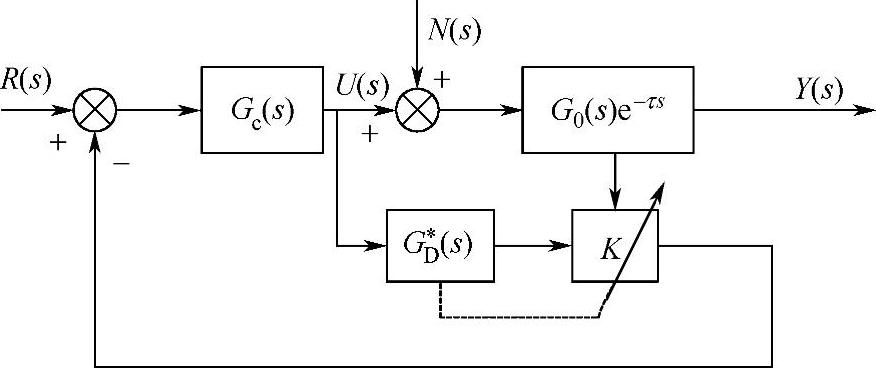
图7-52 可变反馈增益的补偿系统等效框图

在实际情况下，预估器模型往往与实际过程模型的增益存在偏差，若广义对象的增益由K₀增大到K₀+ΔK，则除法器的输出A/B＝（K₀+ΔK）/K₀。假设实际对象其他参数不变，此时比例微分中微分不起作用，其输出也是（K₀+ΔK）/K₀，则乘法器输出变为（K₀+ΔK）G₀（s）。可见系统反馈信号也变化了ΔK，相当于预估模型的增益变化了ΔK。此时，增益自适应补偿系统变成反馈增益可变的复杂控制系统，其等效框图如图7-52所示。

大量的数字仿真和模拟实验表明：在负载扰动作用下，增益自适应补偿控制方案优于Smith预估补偿控制方案，而在给定值变化时，Smith预估补偿控制方案优于增益自适应补偿控制方案。

5.改进型Smith补偿控制

Smith预估补偿控制采用预估器抵消闭环特征方程中出现的时滞项。增加一个合适的补偿控制器使时滞项对系统的影响大大减小，可出现各种各样的Smith补偿控制改进方案。将模型失配的差值作为补偿控制器的输入构成反馈控制，如图7-53所示。

系统输出与给定值和扰动信号之间的传递函数为

图7-53 改进型Smith补偿控制方案一

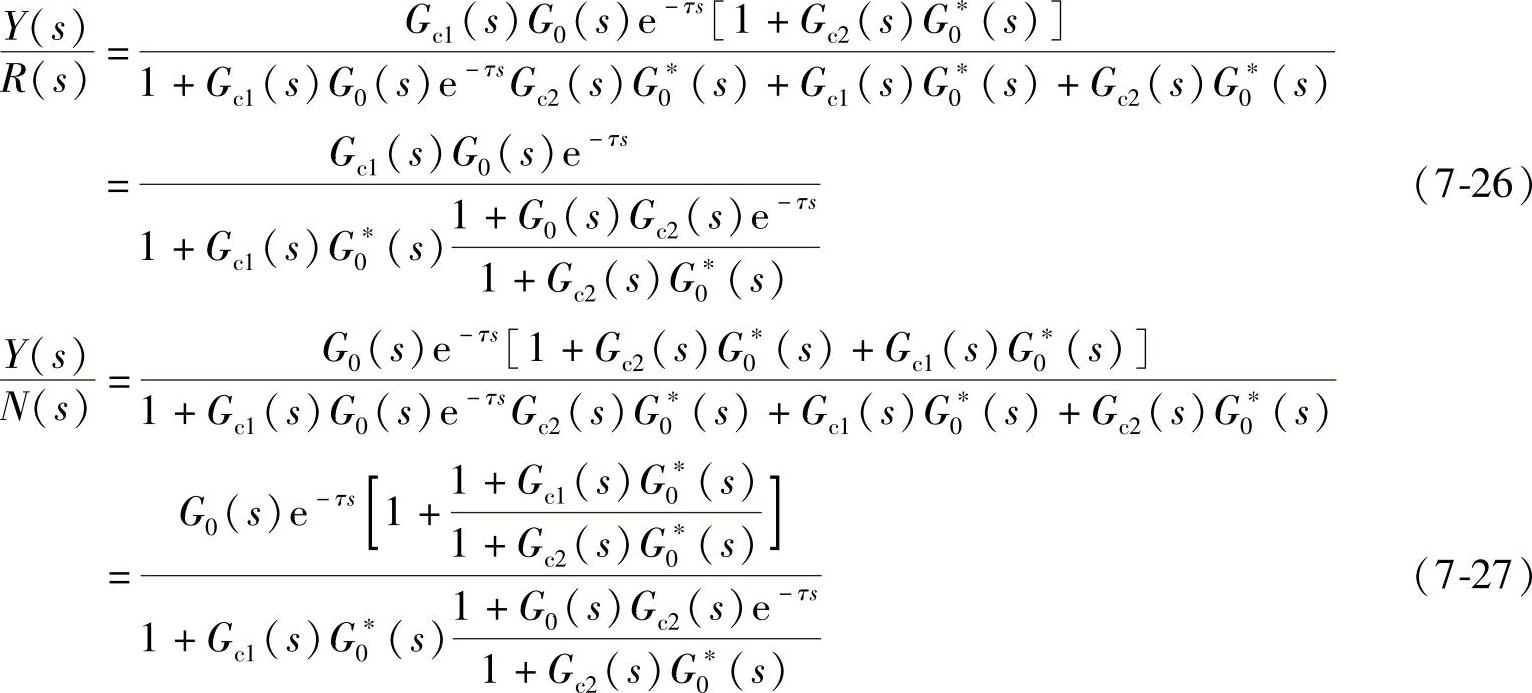
系统的特征方程为

如果选择G_c2（s）的模足够小，则

1+G₀（s）G_c2（s）e-τs≈1，1+G_c2（s）G₀∗（s）≈1

闭环系统的特征方程近似为

D（s）＝1+G_c1（s）G₀∗（s）＝0

系统的稳定性与补偿控制器无关，与被控对象的时滞无关。由式（7-26）和式（7-27）可以看到，系统对模型参数的变化不敏感，且模型不含时滞。

对于一阶惯性加纯滞后的被控对象，G₀（s）e-τs＝2e^-4s/（4s+1），当模型参数失配时（假设K₀与K₀∗相差为4），为了使系统无静差，控制器均选择为PI规律，参数整定采用试探观测法，主控制器的参数K_P＝0.1、T_I＝12.5，补偿控制器的参数K_P＝1、T_I＝80。

当系统在幅值为5的阶跃信号和幅度为0.5的随机干扰作用下时，采用Smith预估补偿控制方案和改进型Smith补偿控制方案的仿真框图如图7-54所示，对应的响应曲线如图7-55所示，依次为随机扰动、模型精确匹配Smith预估补偿控制、模型失配Smith预估补偿控制和模型失配改进型Smith补偿控制响应曲线。

由图7-55可知，虽然系统模型失配很严重，系统所受的干扰也较大，但是采用改进型Smith补偿控制方案后系统响应较为理想，系统对模型参数的变化不敏感。

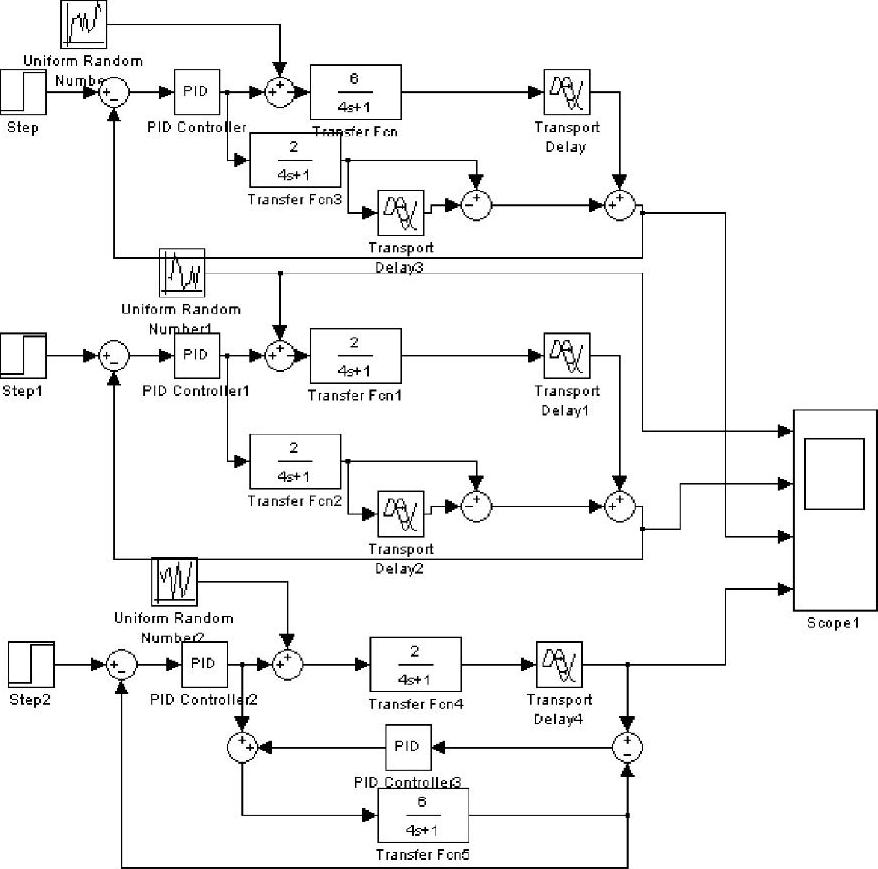
图7-54 改进型Smith补偿控制方案的仿真框图

图7-55 控制系统阶跃响应曲线