前馈控制系统参数整定技巧

前馈控制器参数的整定取决于被控对象的特性和扰动通道的特性，若模型确定则控制器参数也就确定了。但是，由于特性建模的精度、测试工况与在线工况的差异，以及前馈控制装置的精度等，使得控制效果并不那么理想。因此，必须对前馈控制器参数进行在线整定。

目前在实际系统中，应用较为广泛的是前馈-反馈控制方式，反馈控制可保证系统的最终控制精度，并且可以降低对前馈控制的要求，使前馈控制器可以选择比较简单的形式和动态特性。同时又可采用前馈控制来抵消一些主要干扰，减轻了反馈控制的负担，使被控量不致出现过大的动态偏差。在整定前馈-反馈控制系统时，反馈回路和前馈控制分别整定，一般先反馈后前馈，且两者基本独立。反馈控制器按反馈控制系统整定原则进行整定，前馈控制器直接按抵消干扰对被控变量的影响来整定。

这里以前馈控制模型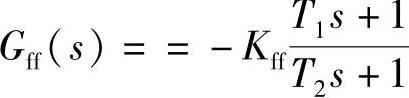为例，讨论控制器参数K_ff及T₁和T₂的工程整定方法。

1.K_ff的整定

静态参数K_ff是前馈控制器中最基本的参数，在工程实际中常采用开环整定法及闭环整定法。

（1）开环整定法

开环整定法是在前馈-反馈系统中将反馈回路断开，使系统处于单纯静态前馈控制状态下，施加干扰信号n（t），K_ff值由小逐步增大，直到系统的被控制量回到设定值，即直到系统完全补偿为止。此时，所对应的K_ff值为最佳整定值。在整定过程中，应力求使系统工况稳定，减少其他干扰对被控变量的影响。

（2）闭环整定法

闭环整定法分为在前馈-反馈运行状态下和反馈运行状态下整定K_ff。

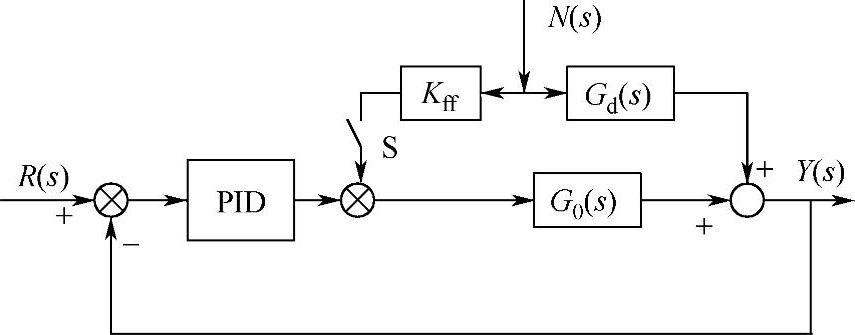
图7-10 K_ff闭环整定法系统框图

1）前馈-反馈运行状态下整定K_ff，整定法系统结构图如图7-10所示。将开关S闭合，使系统处于前馈-反馈运动状态，施加干扰信号，将K_ff由小到大逐渐改变，直到得到满意的补偿过程为止。K_ff对控制过程的影响如图7-11所示。图7-11a为无前馈作用；图7-11b为补偿作用欠缺，此时整定的K_ff值小；图7-11c为补偿合适，整定的K_ff适当；图7-11dK_ff值过大，则造成过补偿。

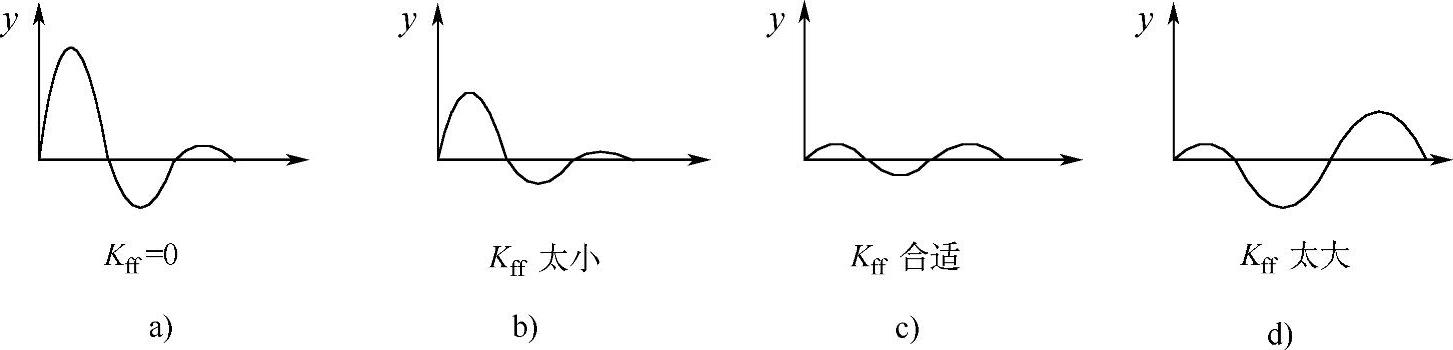
图7-11 K_ff大小对控制过程的影响

假设G₀₁（s）＝e^-10s/（15s+1）、G₀₂（s）＝e^-50s/（60s+1）、G_d（s）＝1/（5s+1），整定反馈控制器PI的参数为K_P＝0.97、T_I＝187s，前馈-反馈运行状态下整定K_ff的Simulink仿真框图如图7-12所示。

在干扰信号为单位阶跃信号时，逐步调整静态系数K_ff使系统的输出响应平稳，不同K_ff下系统的响应曲线如图7-13所示。

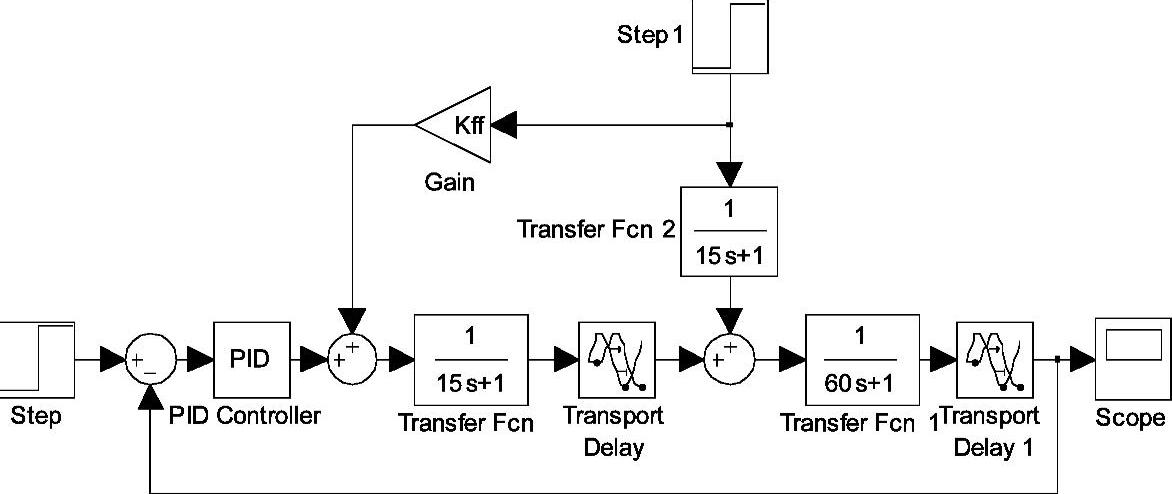
图7-12 闭环整定K_ff的Simulink仿真框图

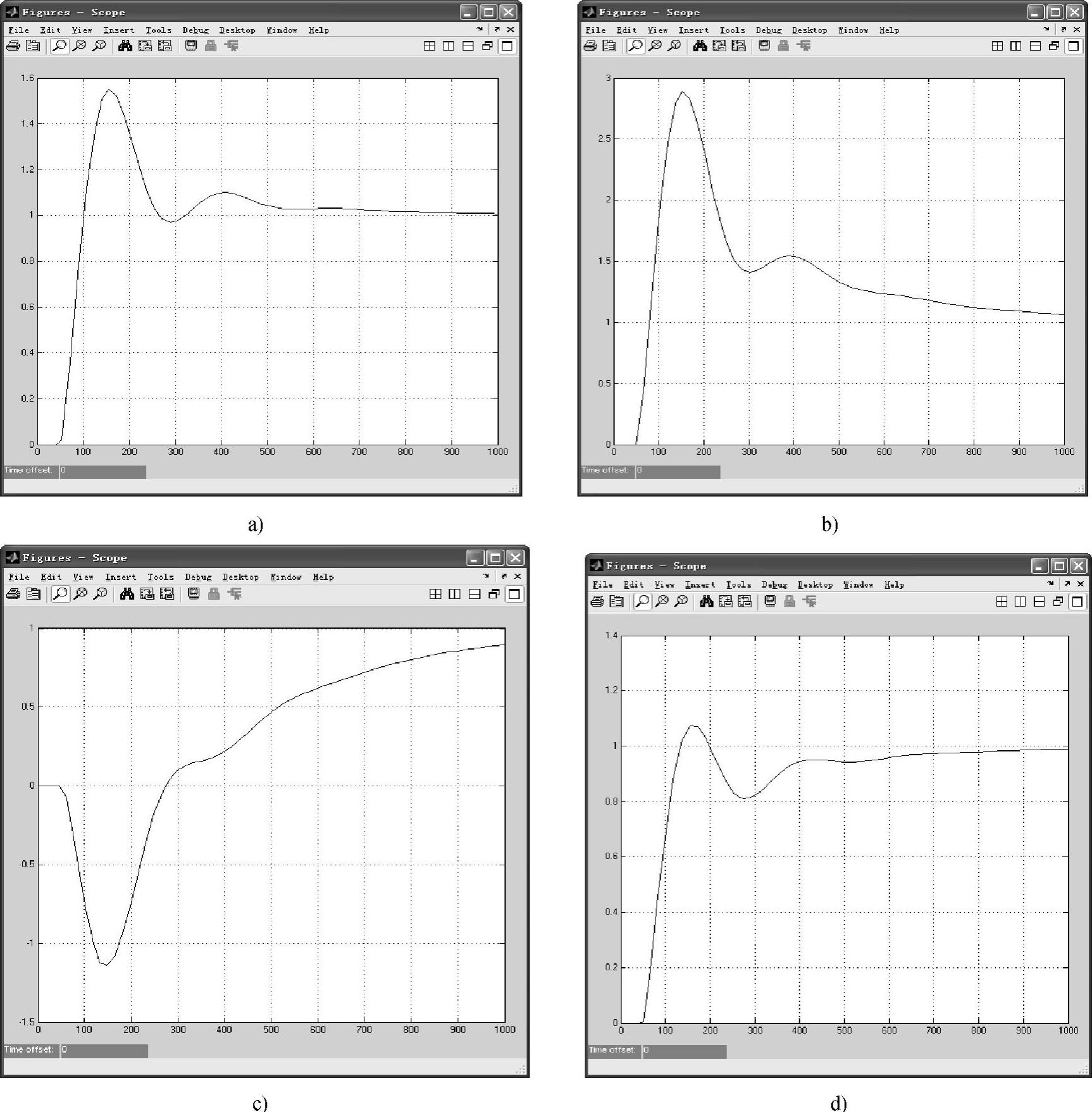
图7-13 静态前馈系数整定过程曲线

a）PID控制下输出（K_ff＝0） b）前馈补偿方向错误（K_ff＝2） c）前馈补偿方向正确但幅度偏大（K_ff＝-4） d）前馈补偿较佳（K_ff＝-0.7）

2）反馈运行状态整定K_ff，整定步骤如下：

①将图7-10中的开关S打开，使系统处于反馈运行状态。待系统运行稳定后，记录下干扰变送器的输出Y_n0和反馈控制器的稳态输出值Y_c0。

②对干扰n施加一增量Δn，等到反馈控制系统在Δn作用下，被控量重新回到设定值时，再记下干扰变送器的输出Y_n和反馈控制器的稳态输出值Y_c。

③计算前馈控制器的静态放大系数K_ff为

④将K_ff的计算值设置在前馈控制器上，合上开关。在前馈-反馈控制系统中，施加扰动n，观测系统的响应过程。若不够理想，适当调整K_ff，直到响应曲线符合要求为止。

这种整定方法需要注意两点：一是反馈控制器应具有积分作用，否则在干扰作用下无法消除被控变量的静差；二是要求系统工况尽可能稳定，以消除其他干扰的影响。

假设G₀₁（s）＝e^-10s/（15s+1）、G₀₂（s）＝e^-50s/（60s+1）、G_d（s）＝1/（5s+1），整定反馈控制器参数为K_P＝0.97、T_I＝187s，反馈运行状态下整定K_ff的Simulink仿真框图如图7-14所示。

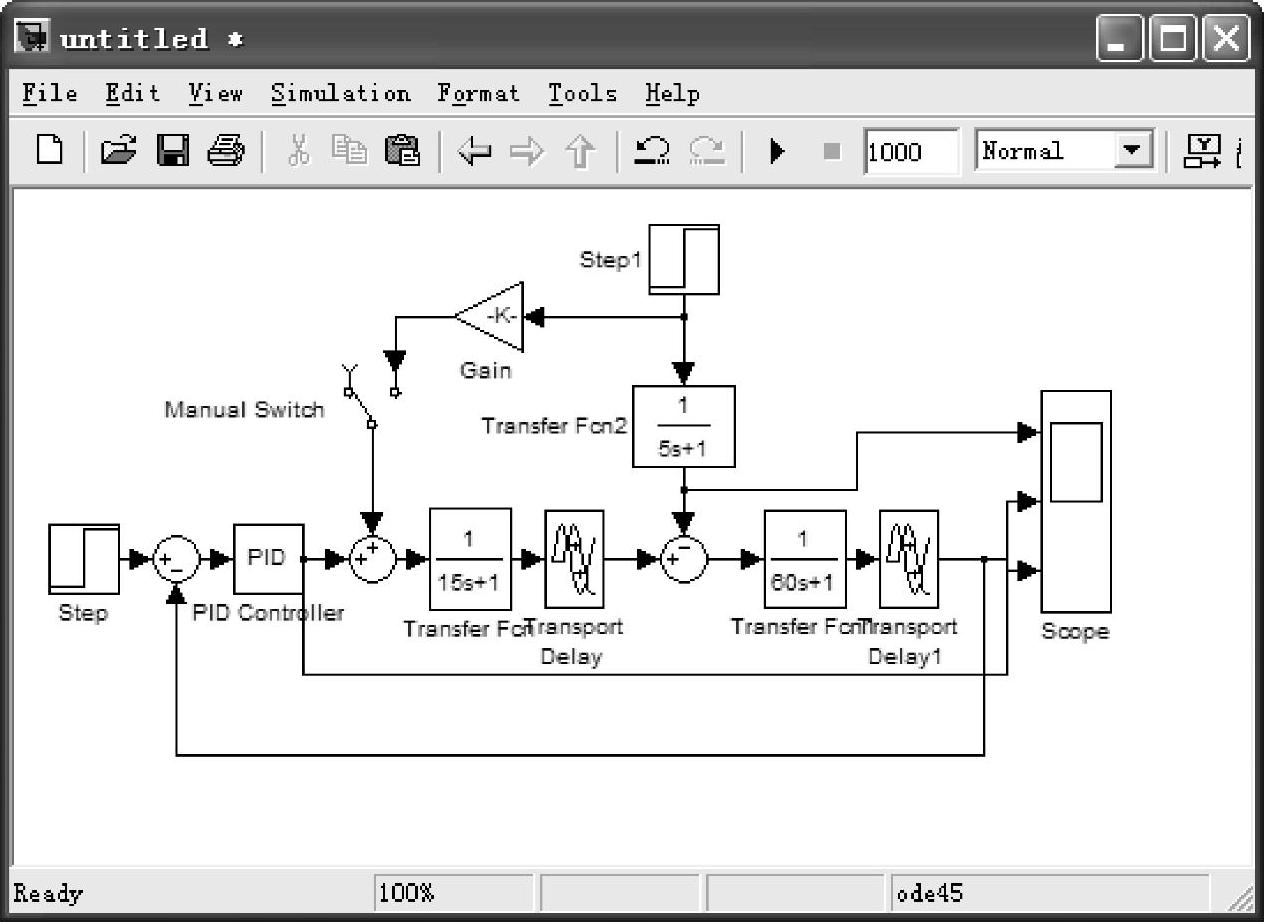
图7-14 反馈运行状态下整定K_ff的Simulink仿真框图(https://www.xing528.com)

给定信号为单位阶跃，扰动信号突变时系统干扰变送器的输出曲线、反馈控制器的输出曲线和系统输出响应曲线如图7-15所示。

计算静态系数K_ff＝（Y_c-Y_c0）/（Y_n-Y_n0）＝（2-1）/（1-0）＝1，前馈-反馈系统中K_ff＝1时，系统给定信号和突加干扰信号作用下的响应曲线如图7-16所示。

2.T₁、T₂参数的整定

前馈控制器的动态参数整定主要途径是经验或定性分析，同时借助在线运行曲线来判断与整定T₁、T₂的值。

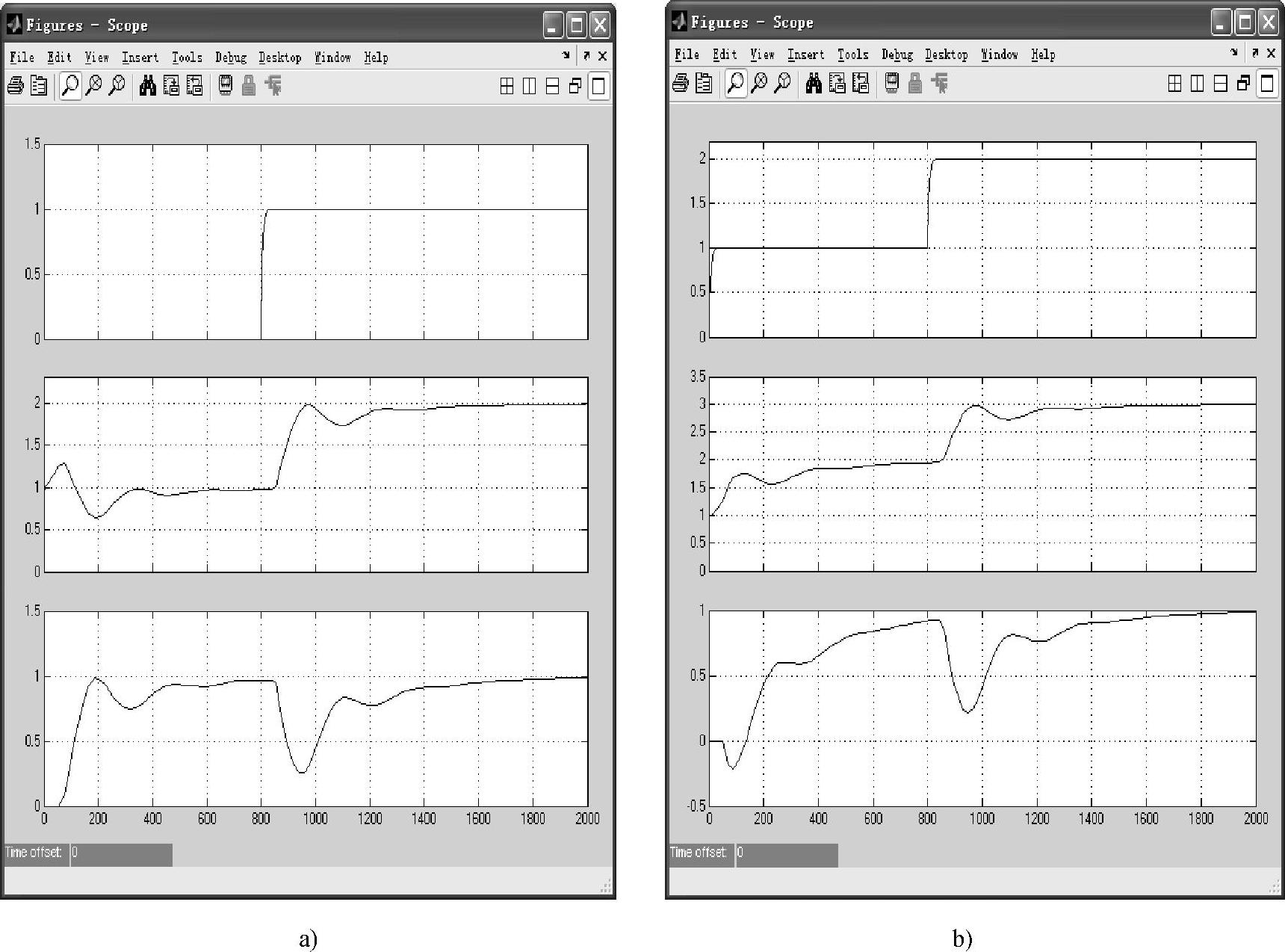
图7-15 扰动突变下干扰变送器、反馈控制器和系统输出的曲线

a）干扰由0突变为1的输出曲线 b）干扰由1突变为2的输出曲线

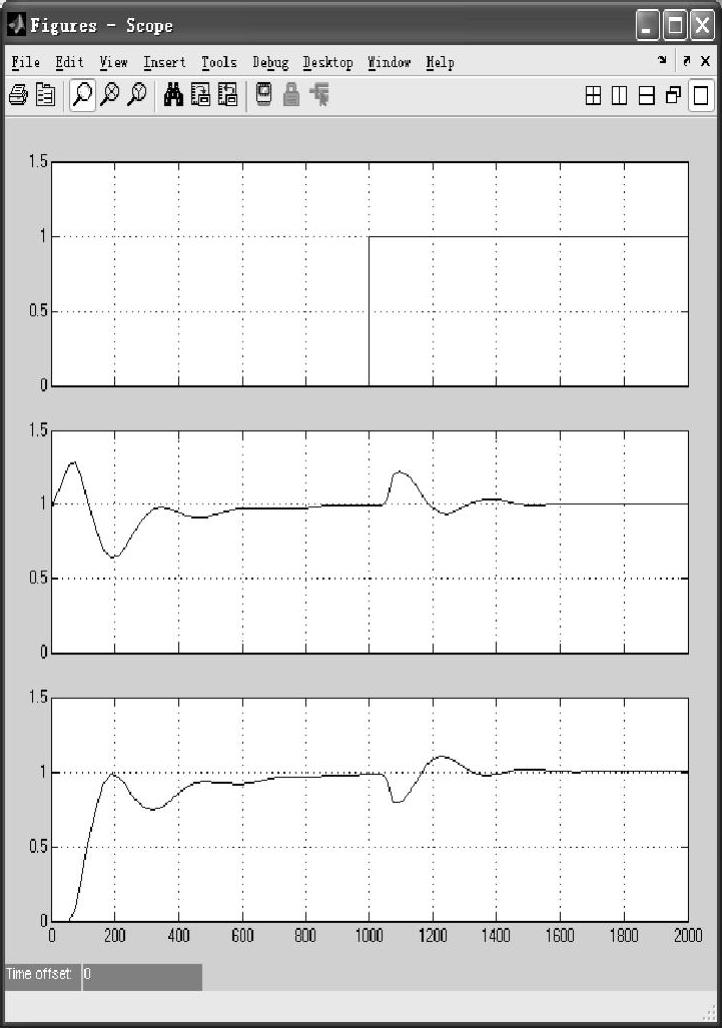
图7-16 前馈-反馈系统输出响应曲线

动态参数T₁、T₂的值决定了系统动态特性补偿的程度，当T₁＞T₂时，前馈控制器在动态补偿过程中起超前作用；当T₁＜T₂时，前馈控制器在动态补偿过程中起滞后作用；当T₁＝T₂时，动态补偿不起作用。而当T₁过小或T₂过大时，系统会产生欠补偿现象，未能有效地发挥前馈补偿的功能；当T₁过大或T₂过小时，系统会产生过补偿现象，所得到的控制效果甚至比单纯的反馈控制的品质还差；当T₁、T₂分别接近或等于对象控制通道和干扰通道的时间常数时，过程的控制质量最佳，此时补偿合适。

由于过补偿会破坏控制过程，甚至运行到系统不能允许的地步。相反，欠补偿是寻求合理的前馈控制器动态参数的途径。欠补偿的结果总比反馈过程好一些，因此动态参数T₁、T₂的整定应从欠补偿开始，并逐步强化前馈作用，即增大T₁或减小T₂，直到出现过补偿的趋势再略减弱前馈作用，便可获得满意的控制效果。该整定方法实际上是看曲线调参数的经验法。

假设G₀₁（s）＝e^-10s/（15s+1）、G₀₂（s）＝e^-50s/（60s+1）、G_d（s）＝1/（5s+1），整定反馈控制器参数为K_P＝0.97、T_I＝187s，静态前馈控制的K_ff＝1.2，时间常数T₁、T₂的整定采用动态特性曲线法，Simulink仿真框图如图7-17所示。

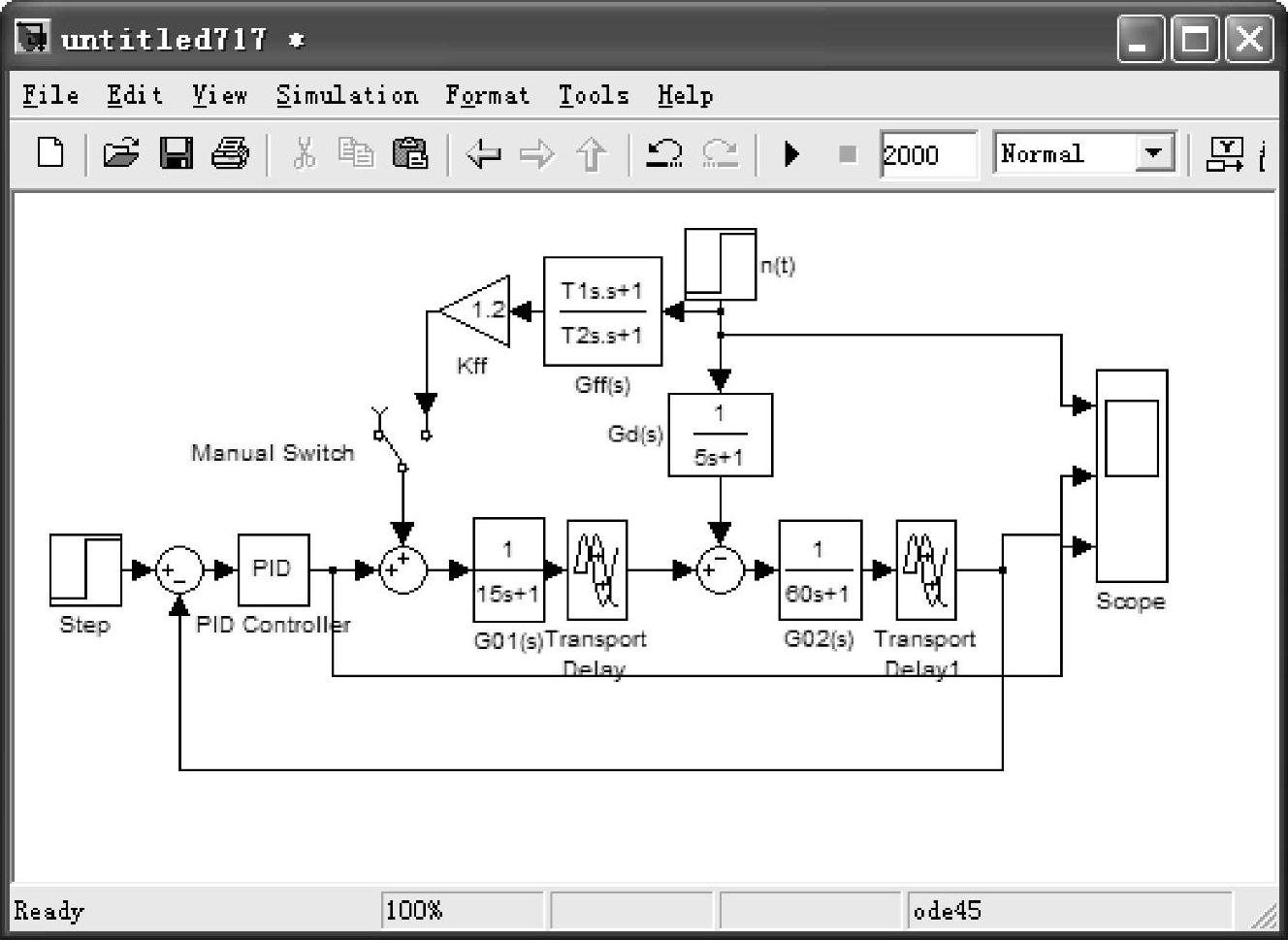
图7-17 动态特性曲线法的Simulink仿真框图

当干扰为零时（n＝0），系统的单位阶跃响应曲线如图7-18点画线所示；干扰为单位阶跃信号无前馈补偿时（n（t）＝1（t），G_ff（s）＝0）单位阶跃响应曲线如图7-18虚线所示，动态补偿调节T₁＝T₂＝1（动态补偿不起作用）系统的响应曲线如图7-18实线所示。

根据被控变量的响应曲线对T₁、T₂的值进行整定。初选择T₁＝50，T₂＝5时，系统为无前馈补偿时纯反馈系统的输出和加动态前馈补偿控制器的输出响应曲线如图7-19所示，从曲线看到采用T₁＞T₂动态超前补偿作用，控制效果比单纯的反馈控制的品质还差。

为此，选择T₁＝5、T₂＝50时，系统无动态补偿时输出响应曲线和动态前馈控制的输出响应曲线如图7-20a所示。从曲线看到采用T₁＜T₂动态滞后补偿作用，控制效果比单纯的反馈控制的品质要好，但补偿的时间太长。缩小T₁和T₂的差值，选择T₁＝5、T₂＝35时，系统的响应曲线如图7-20b所示，表明补偿朝合理方向变化。进一步调整T₁＝5，T₂＝15，系统的响应曲线如图7-20c所示。进一步调整T₁＝10、T₂＝15，系统的响应曲线如图7-20d所示，前馈补偿效果最佳。

综合考虑，最佳动态前馈控制器为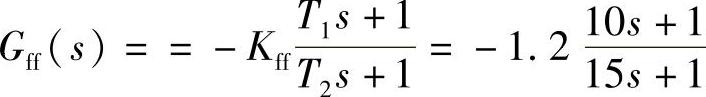，前馈-反馈控制系统在设定值为10、系统施加幅值为1的随机干扰，系统的Simulink仿真框图如图7-21所示，随机扰动信号、动态前馈控制器的输出、动态前馈-反馈系统的输出响应曲线如图7-22所示。

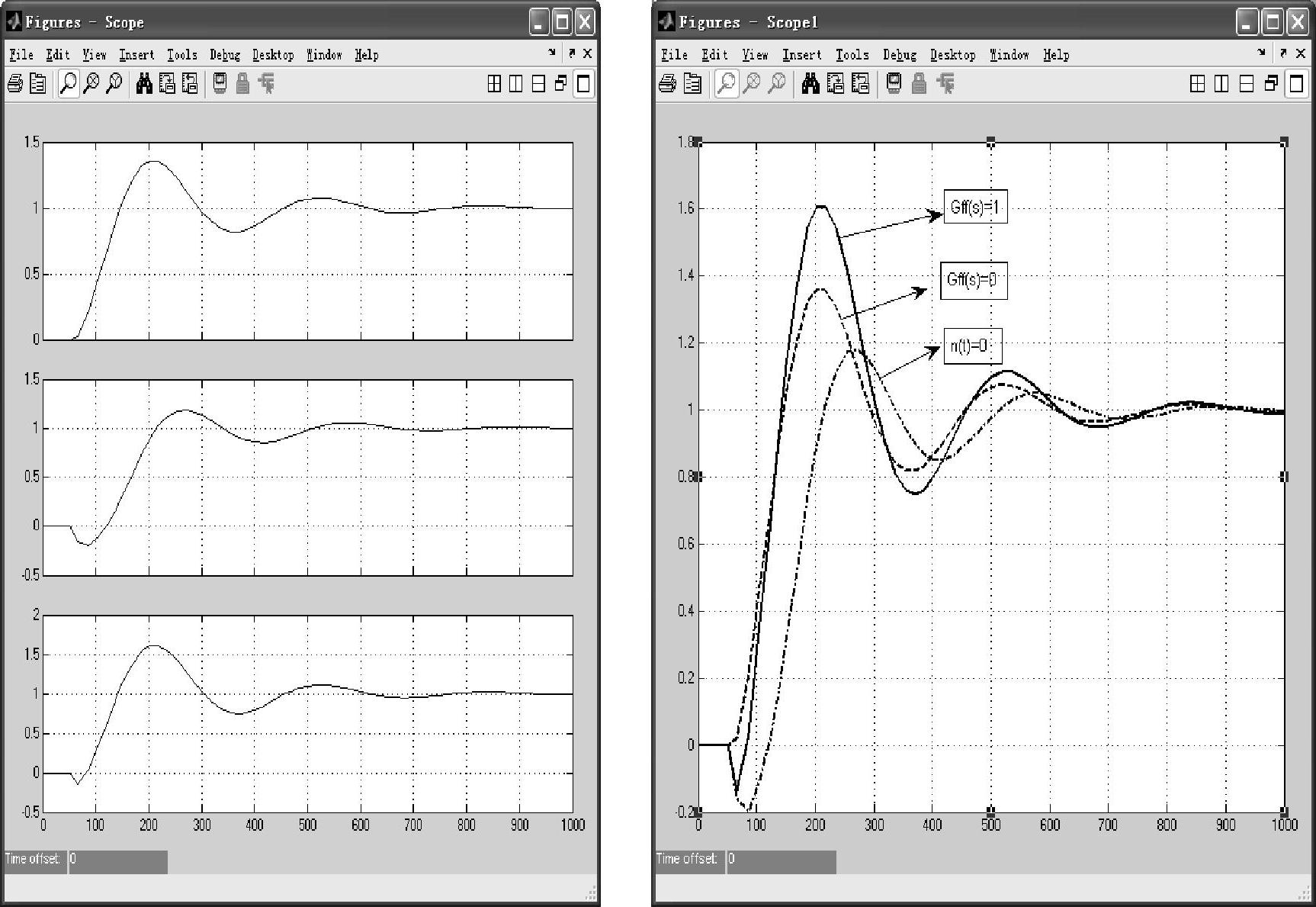
图7-18 系统的输出响应曲线

图7-19 动态前馈控制系统响应曲线

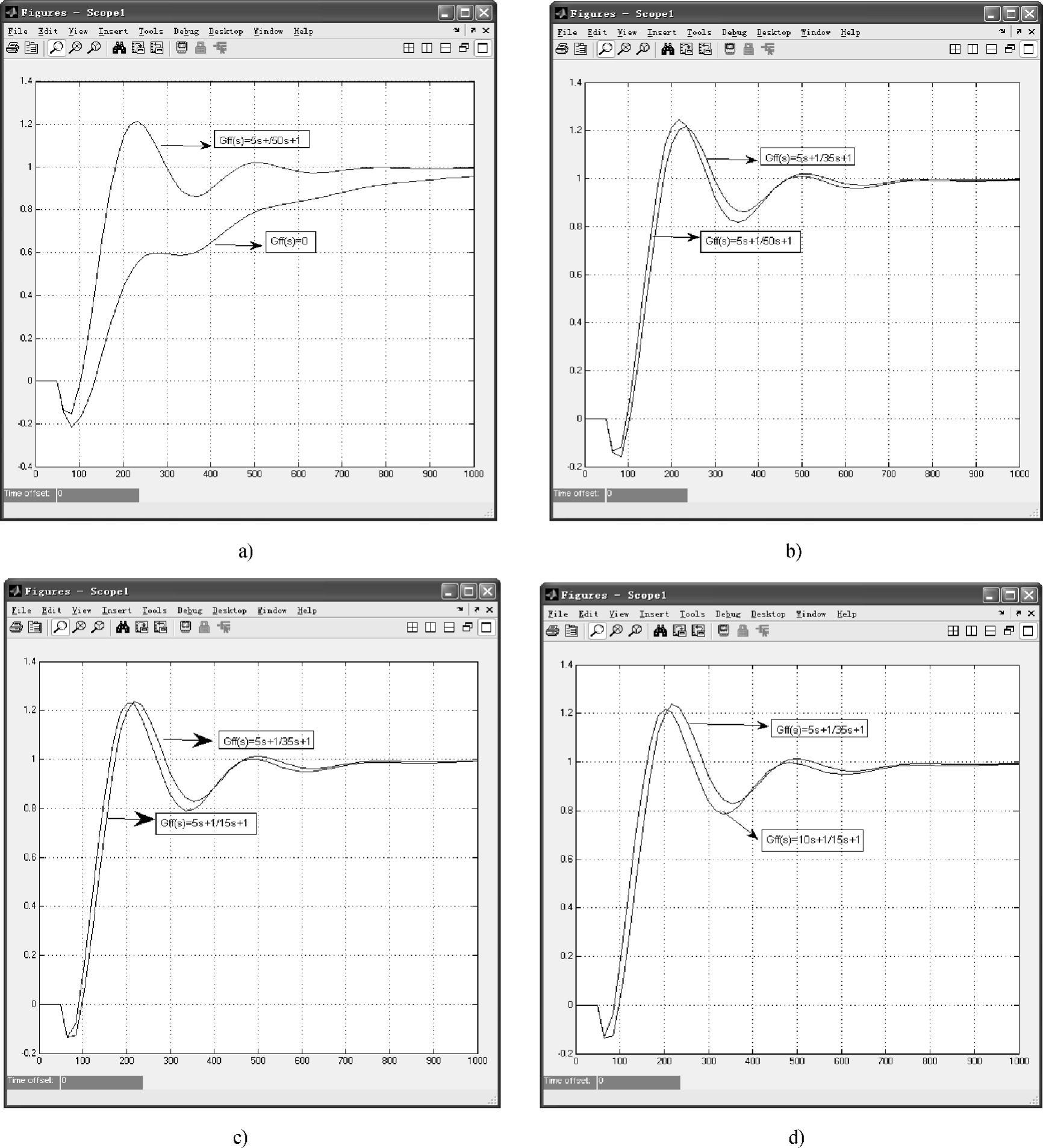
图7-20 动态前馈控制系统响应曲线

a）T₁＝5、T₂＝50 b）T₁＝5、T₂＝35 c）T₁＝5、T₂＝15 d）T₁＝10、T₂＝15

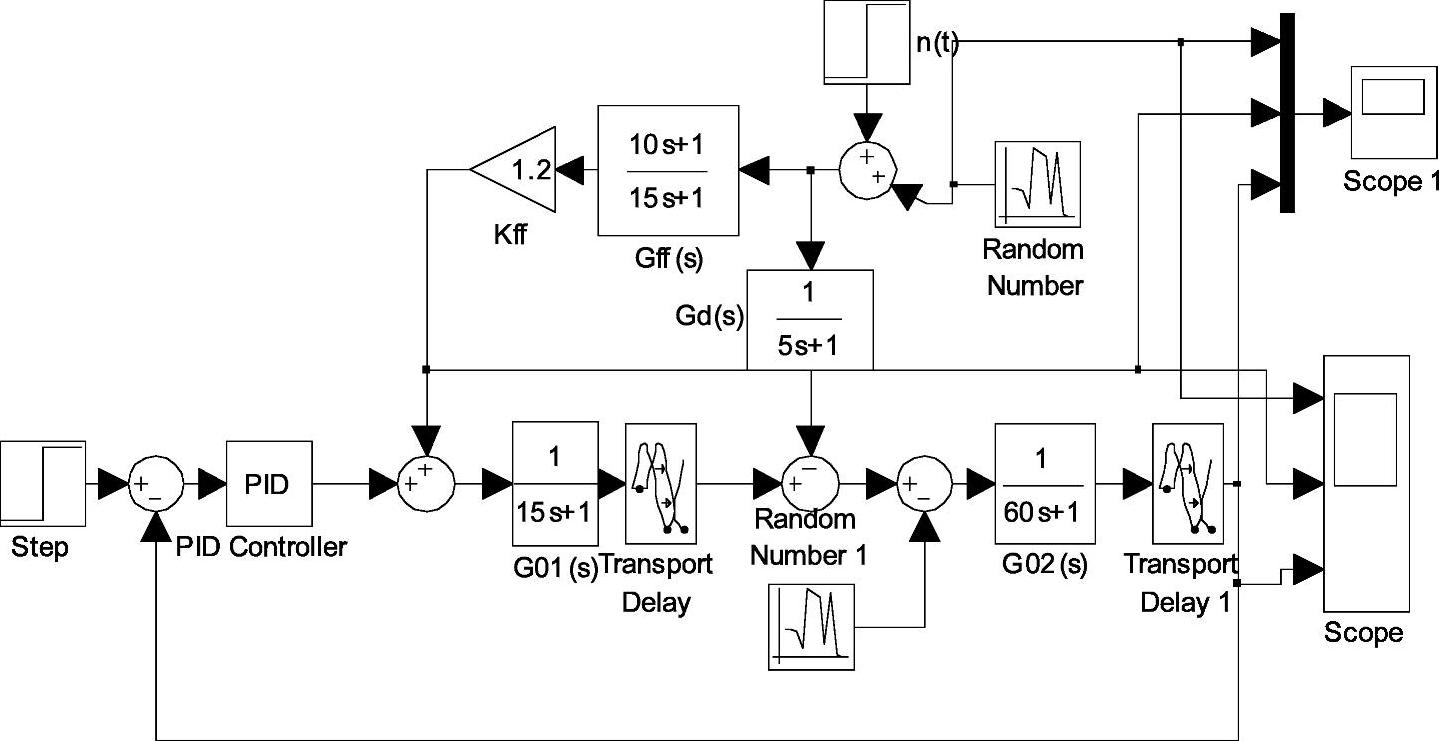
图7-21 控制系统Simulink仿真框图

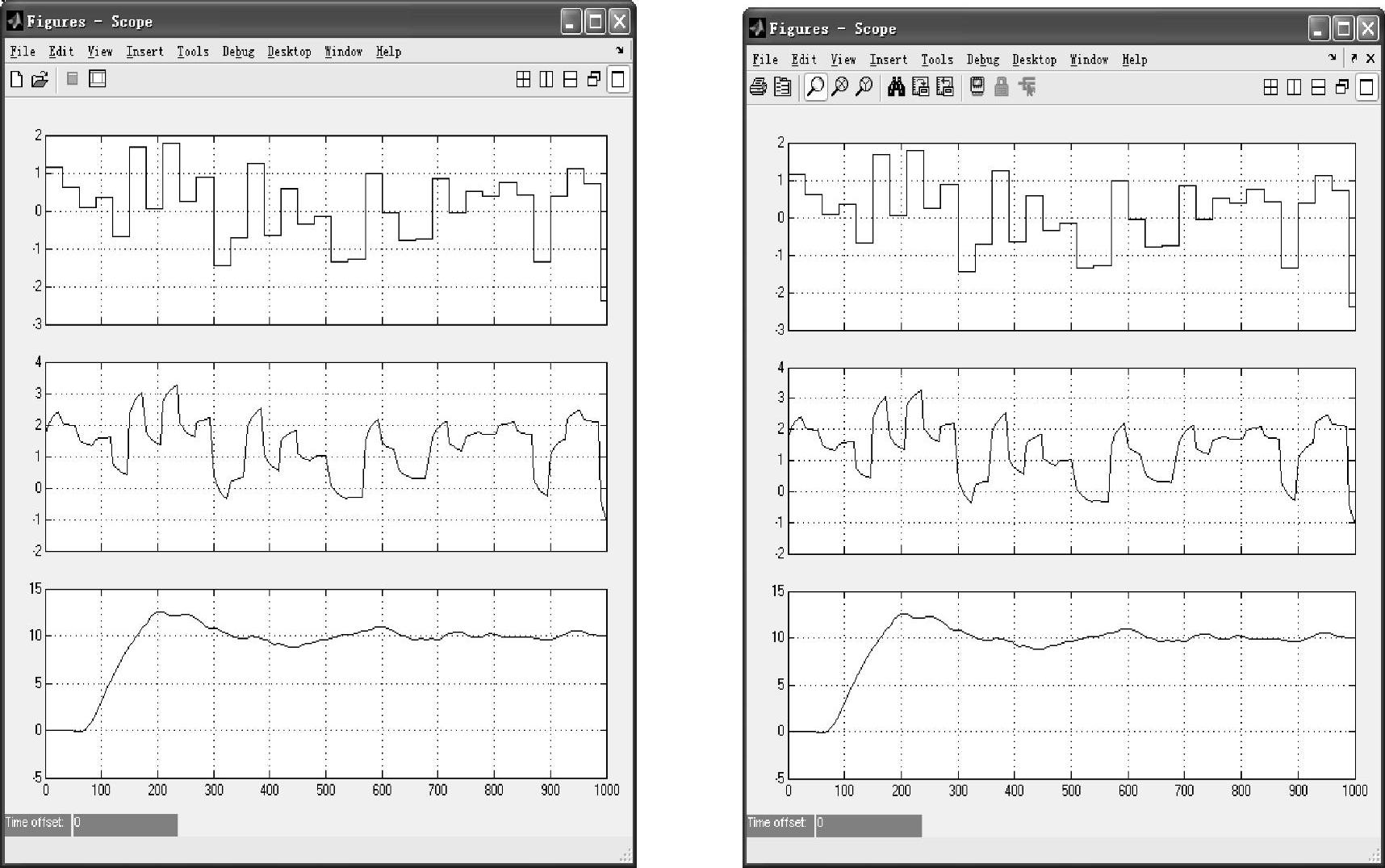
图7-22 控制系统输出响应曲线