串级控制系统克服对象容量滞后的方法

在工业生产中，往往很多被控对象的容量滞后较大，采用单回路控制系统则因为其容量滞后较大、控制通道时间常数大造成控制作用迟缓、系统的超调量大、过渡过程时间长，很难满足生产工艺的要求。

对象容量滞后大、干扰复杂的情况下，采用串级控制系统，选择一个容量较小的被控量组成副回路，使等效副对象的时间常数减小，提高系统的工作频率，加快系统的响应速度，缩短系统的调节时间，获得较好的控制效果。

图5-45 串级控制系统Simulink仿真图

图5-46 串级控制系统输出响应曲线

a）系统的跟踪特性曲线 b）二次干扰作用下输出响应 c）一次干扰作用下输出响应 d）一、二次干扰同时作用下输出响应

例如管式加热炉出口温度与炉膛温度串级控制系统。管式加热炉出口温度单回路控制系统如图5-47所示。

假设原料油出口温度的特性可近似为G_o1（s）＝e^-180s/（30s+1）（30s+1），燃料热值变化对炉膛温度影响特性可近似为G_o2（s）＝e^-18s/（10s+1）（s+1）2。

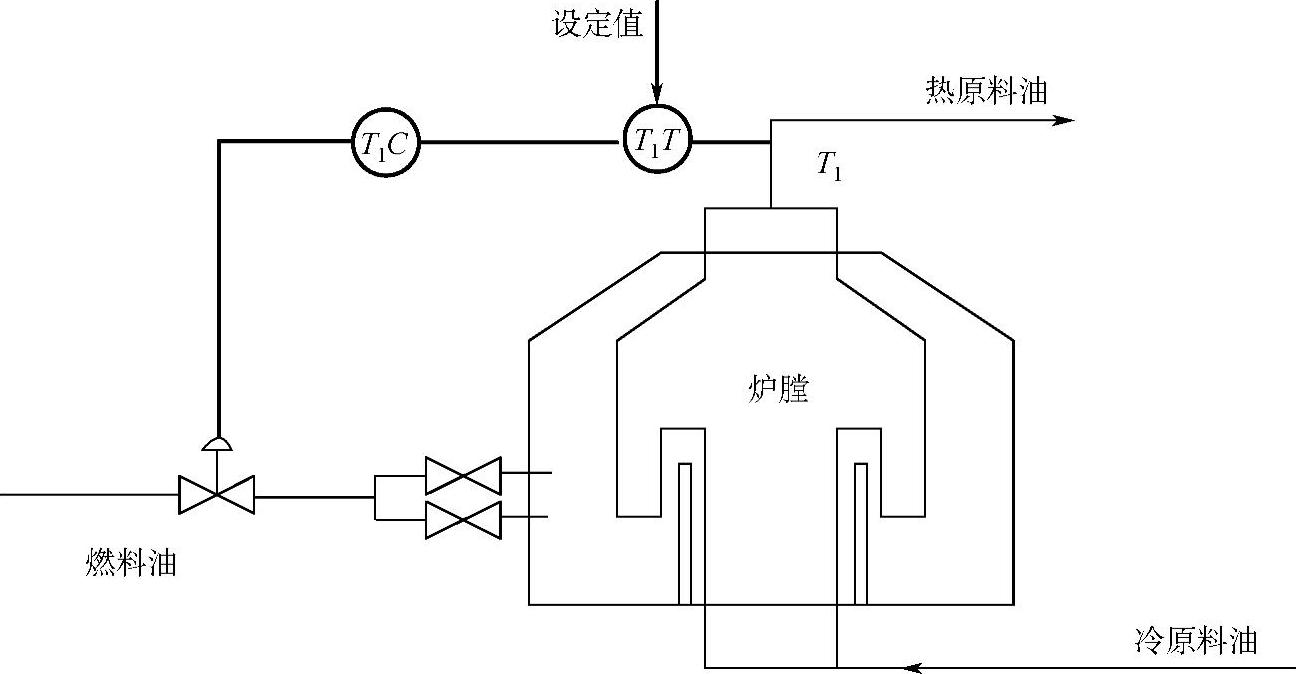
图5-47 管式加热炉出口温度单回路控制系统

采用临界比例度法整定单回路PID控制器参数仿真如图5-48所示，临界比例值K_P＝1.135，临界振荡周期T_K＝540，查表得PID控制时K_P＝0.6676，T_I＝270，T_D＝67.5，系统的阶跃响应曲线如图5-49a所示，动态偏差达23％，调节时间非常长，且系统波动太频繁，难以满足要求，工程中采用优化整定PID参数得K_P＝0.4694，T_I＝240，T_D＝25得单回路系统阶跃响应曲线如图5-49b所示，最佳的动态偏差为14％，系统的过渡过程时间为520min。

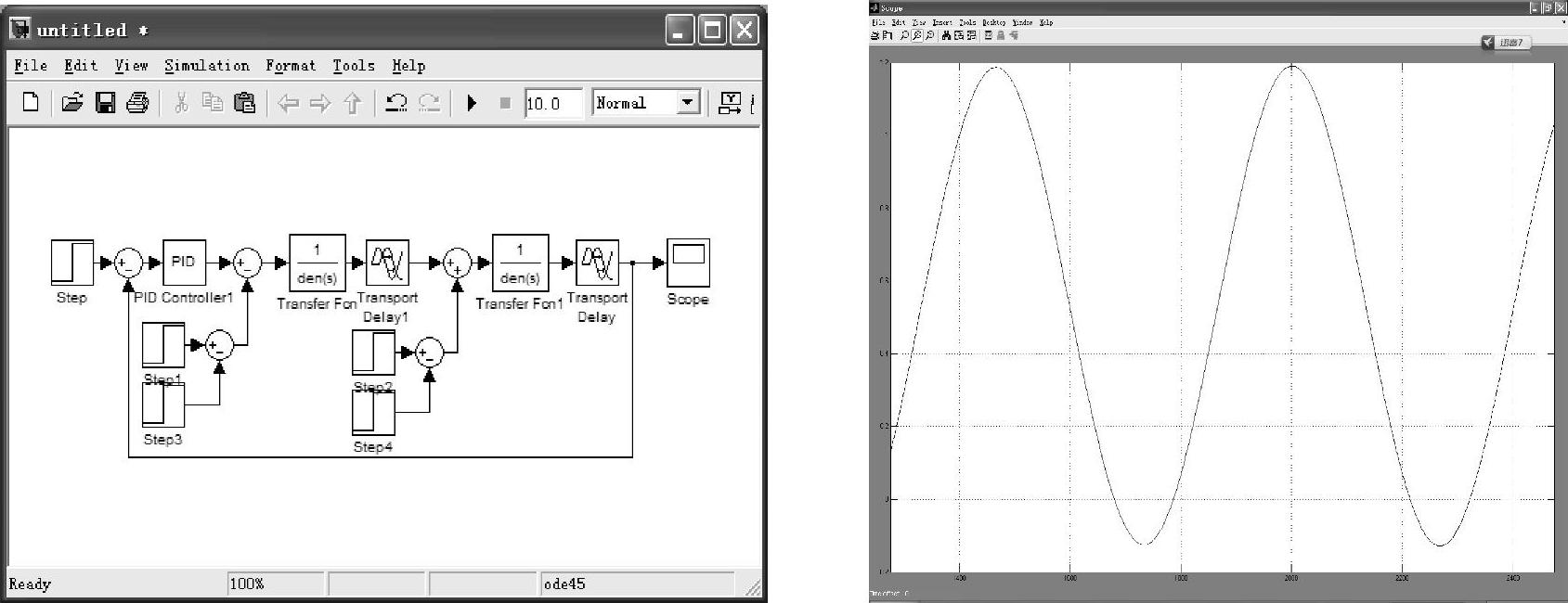
图5-48 单回路控制系统Simulink仿真

从扰动响应来看，给系统突加30％的干扰信号作用分别作用在一次、二次时的抗扰曲线如图5-50所示，系统的调节时间大于13min。

从图5-50可以看到，采用单回路控制原料油出口温度波动比较大，且干扰作用下系统的动态偏差及调节时间均无法满足系统要求。

分析可知原料油出口温度的特性纯滞后时间为3min，时间常数为15min。对象的容量较大，而燃料热值变化对炉膛温度的纯滞后时间为0.3min，时间常数为10s，反映较灵敏。为此，选择炉膛温度作为副变量构成管式加热炉出口温度与炉膛温度串级控制系统，如图5-51所示。

采用两步整定法整定串级控制系统主、副控制器PID的参数，系统Simulink仿真框图如图5-52所示。

(www.xing528.com)

图5-49 单回路系统PID控制的阶跃响应曲线

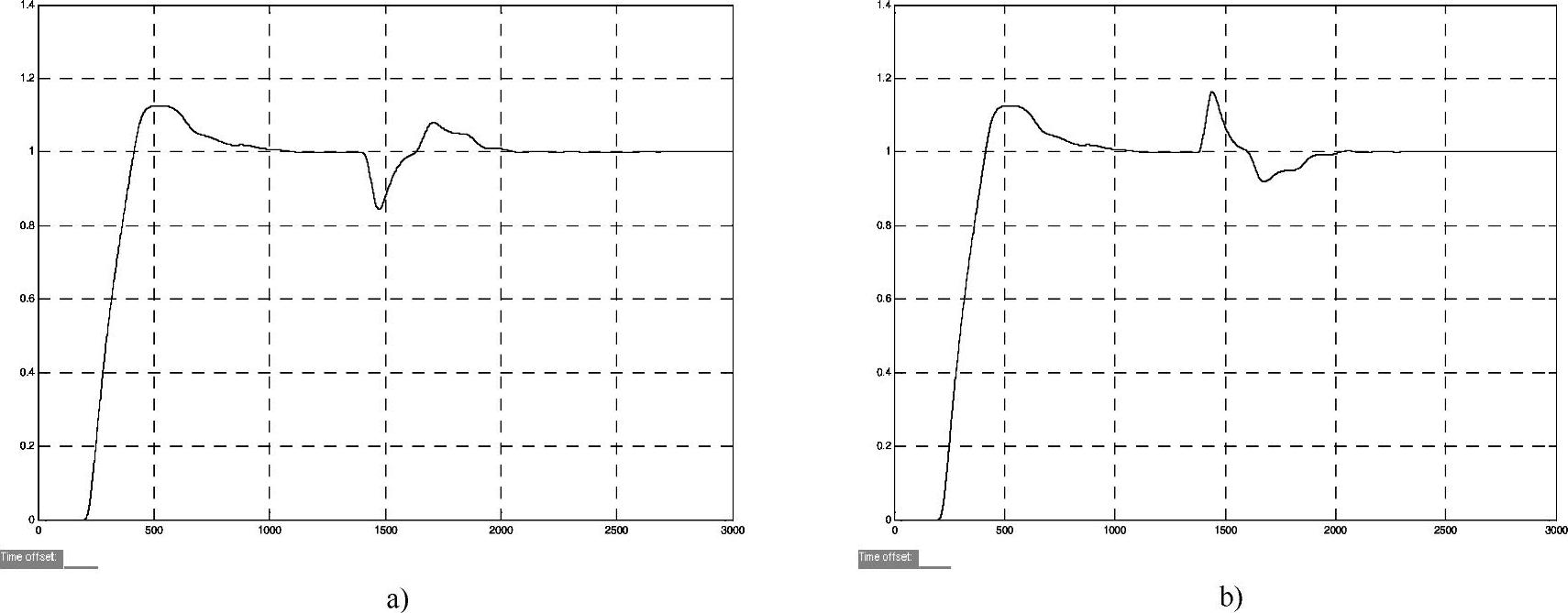
图5-50 干扰作用下系统响应曲线

a）二次干扰作用下输出响应 b）一次、二次干扰同时作用下输出响应

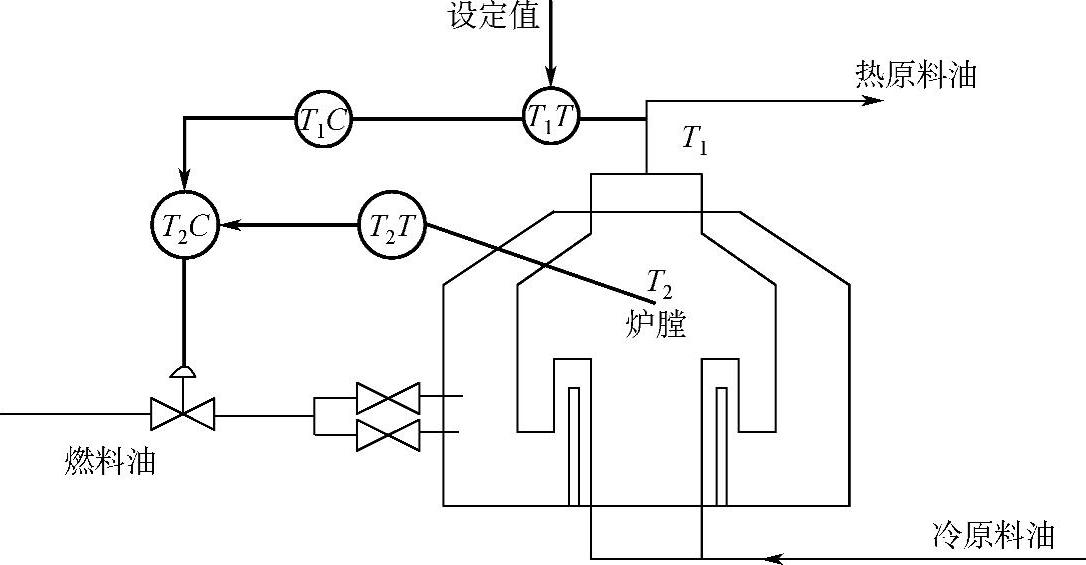
图5-51 管式加热炉出口温度与炉膛温度串级控制系统

首先将主控制器的比例度置于δ_1S＝100％，按单回路系统的衰减曲线法整定副回路，如图5-53所示为副变量满足4∶1衰减的过渡过程曲线，此时的比例度为δ_2S＝86.4％，衰减振荡周期T_2S＝55s，在副控制器的比例度不变的情况下，将副回路看成是主回路的一个环节，用同样的方法将主控制器的比例度由大到小调节，直到主变量出现4∶1衰减的过渡过程曲线如图5-54所示，此时的比例度δ_1S＝117.64％，衰减振荡周期T_1S＝270s。

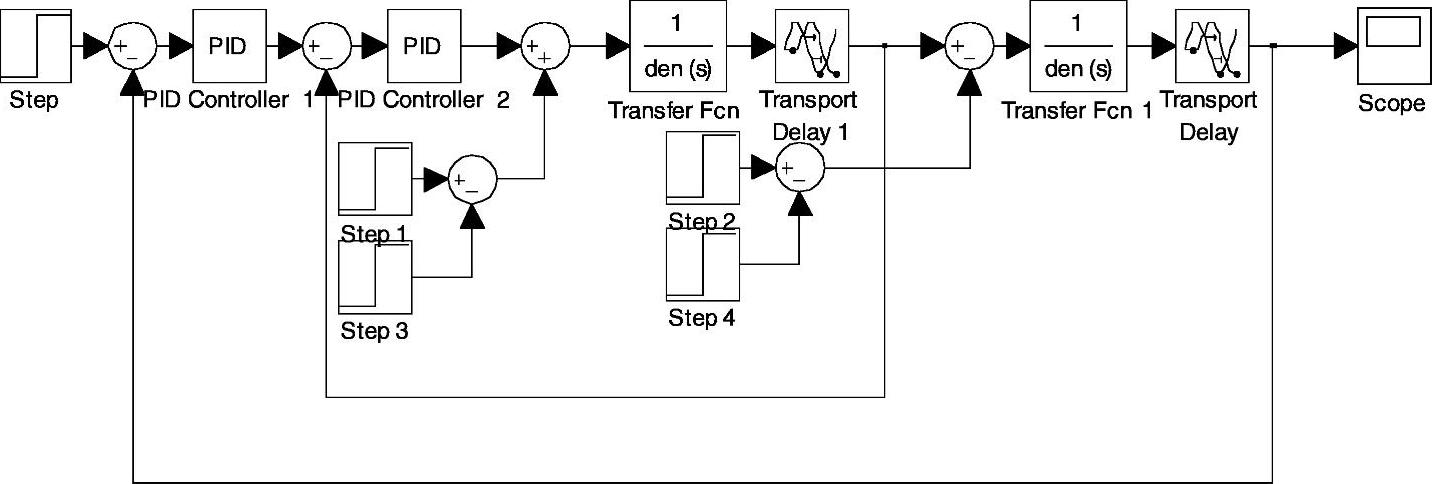
图5-52 串级控制系统Simulink仿真框图

图5-53 副变量呈4∶1响应曲线

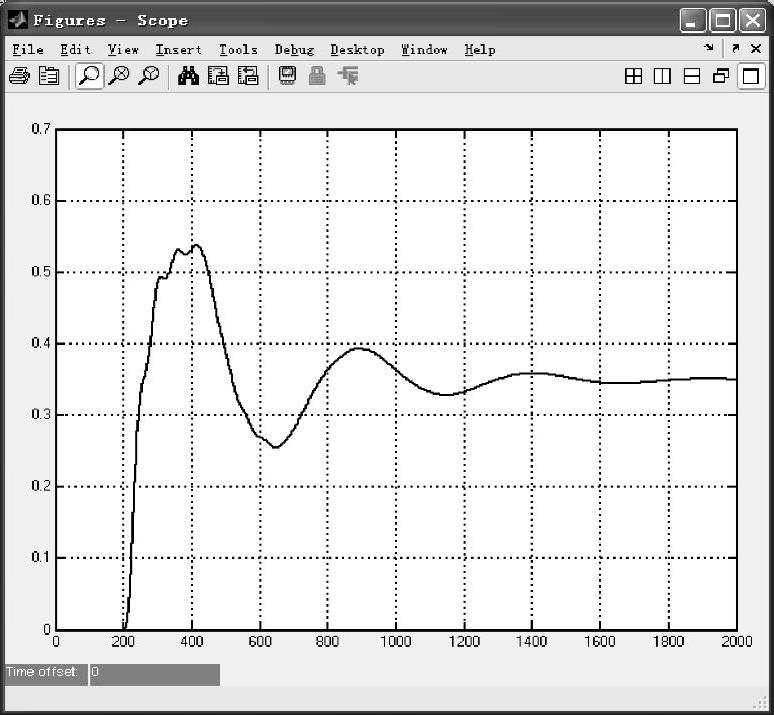
图5-54 主变量呈4∶1响应曲线

根据已求得的δ_1S、T_1S、δ_2S、T_2S的值，按照经验公式且适当修正求得主控制器PID的最佳参数K_P＝0.48、T_I＝270、T_D＝3和副控制器PI的最佳参数K_P＝1.13、T_I＝28，系统的跟踪特性响应曲线如图5-55a所示。

系统稳定运行后在1500s时，施加幅值为30％的一次脉冲扰动信号，系统的输出曲线如图5-55b所示。

系统稳定运行后在1500s时，施加幅值为30％的二次脉冲扰动信号系统的输出曲线如图5-55c所示。

系统稳定运行后在1500s时，施加幅值为30％的一次和二次同时脉冲扰动信号系统的输出曲线如图5-55d所示。