串级控制系统分析及优化建议

串级控制系统在结构上仅仅比简单控制系统多了一个副控制回路，但对系统的影响特别大。

对于同样的被控对象，当采用单回路控制时，系统的框图如图5-13所示。采用串级控制时，系统框图如图5-14所示，图中，主、副被控对象的传递函数分别为G₀₁（s）、G₀₂（s）；主、副控制器的传递函数分别为G_c1（s）、G_c2（s）；主、副检测变送器的传递函数分别为G_m1（s）、G_m2（s）；控制阀的传递函数为G_v（s）。

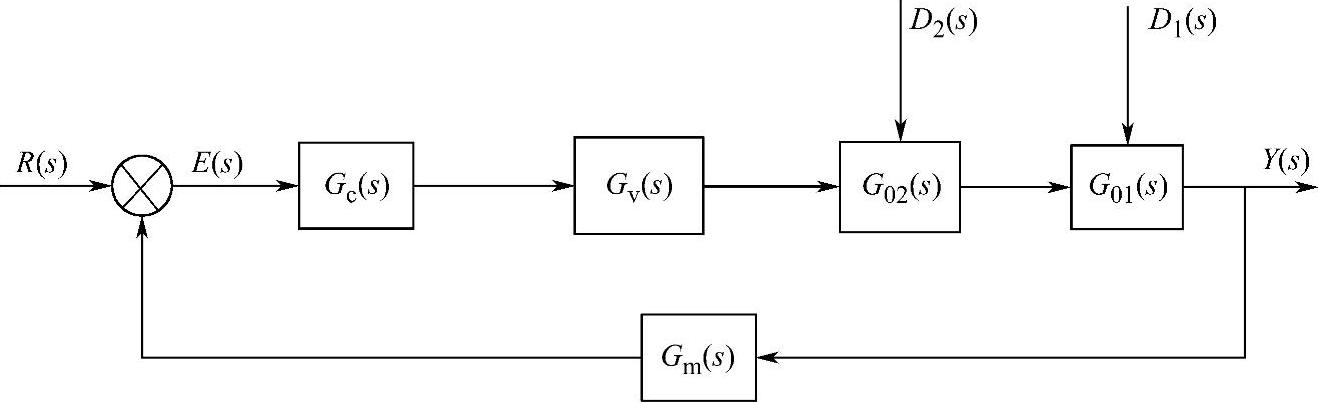
图5-13 单回路控制系统框图

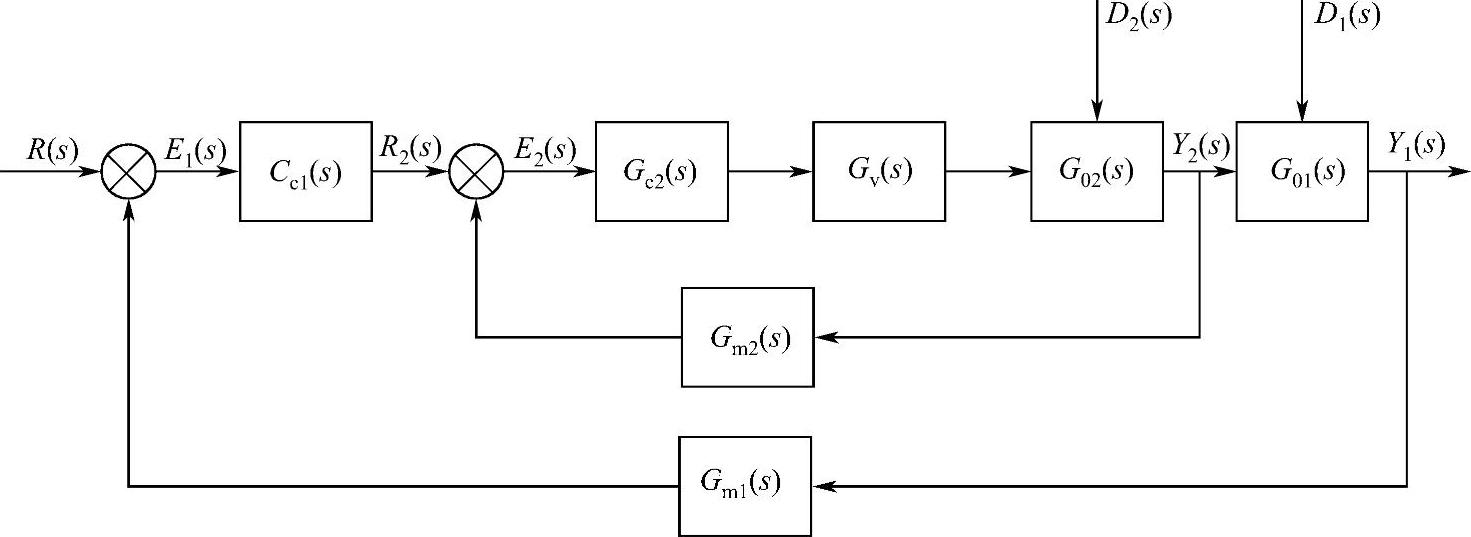
图5-14 串级控制系统的框图

5.2.1.1串级控制系统改善了对象的动态特性减小了被控对象的等效时间常数

如果把整个副回路看作是一个等效副对象，并用G^∗₀₂（s）表示其传递函数，则图5-14可简化为图5-15所示的单回路控制系统，其中

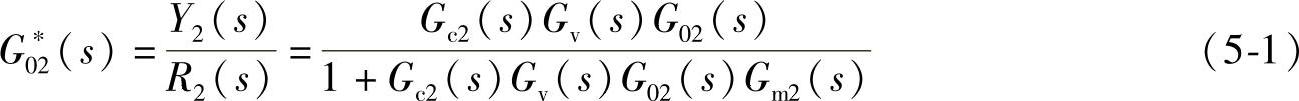
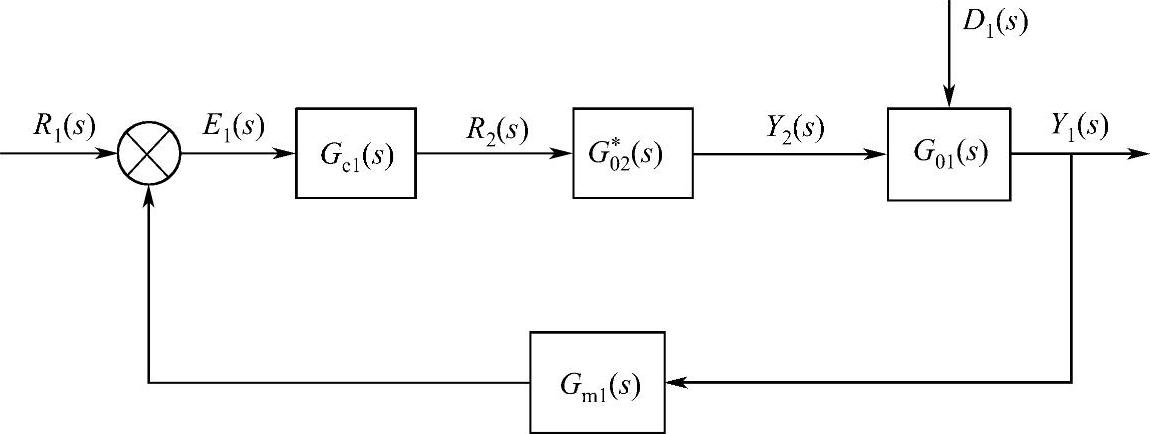
图5-15 串级控制系统的简化框图

根据串级控制系统传递函数简化框图，假设主、副回路各个环节的传递函数分别为

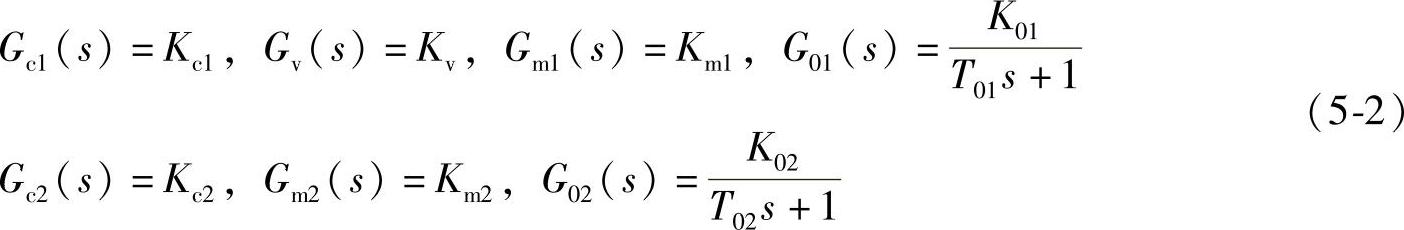
令

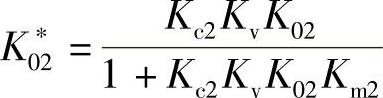
K^∗₀₂为等效副对象的放大倍数。

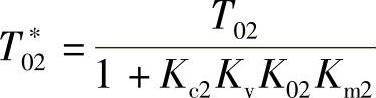
T^∗₀₂为等效副对象的时间常数。

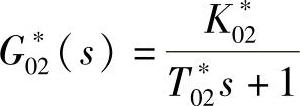
G^∗₀₂（s）为等效副对象的传递函数。

无论在何种情况下，1+K_c2K_vK₀₂K_m2＞1不等式总是成立的，由此得串级控制系统能使等效副对象的时间常数T₀∗₂变小到原来的1/（1+K_c2K_vK₀₂K_m2）倍。时间常数减小意味着副对象的容量滞后减小，使系统的响应速度加快，控制更加及时。同时，对于克服二次干扰的能力也有一定程度的提高。另外，因为副对象时间常数减小，对主回路来说其控制通道的时间也缩短了，克服一次干扰时，比同等条件下单回路控制系统的控制作用更及时，响应速度更快，控制质量有所提高。

等效副回路的放大系数K^∗₀₂减小了1/（1+K_c2K_vK₀₂K_m2），这可使主控制器的增益整定的比单回路控制大些，这对系统抗干扰能力更有利。

5.2.1.2 串级控制系统由于副回路作用对干扰具有较强的抗干扰能力

串级控制系统的框图对二次干扰可等效为如图5-16所示的框图。

串级控制系统在二次干扰D₂作用下系统的传递函数为

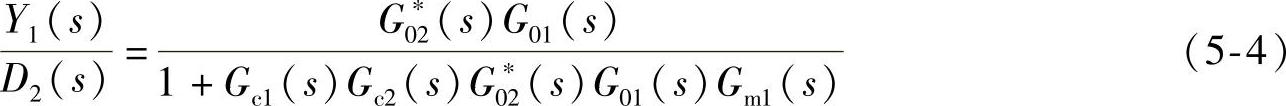
式中

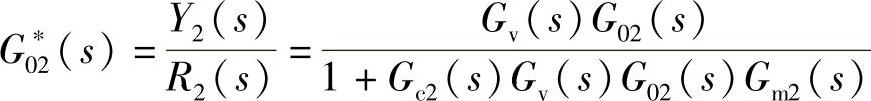
设定值作用下系统的传递函数为

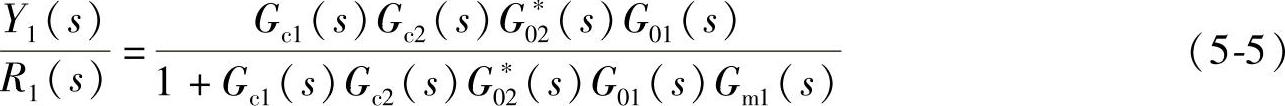
对于一个控制系统，在干扰作用下，控制作用能迅速克服干扰的影响，使被控变量稳定在设定值上，即Y₁的稳态值趋近于零；而在设定值作用下，其控制作用能使被控变量尽快地跟踪设定值的变化，即Y₁的稳态值越趋近于设定值1，则该系统的控制质量就越好，系统的抗干扰能力就越强。当干扰D₂由副回路作用于系统时，综合考虑上述情况，系统对干扰D₂抗干扰能力可以表示为

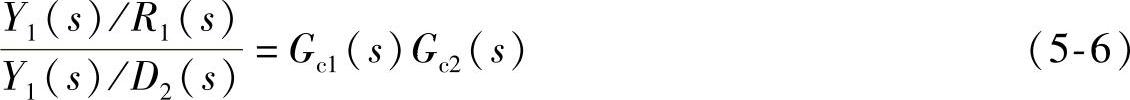
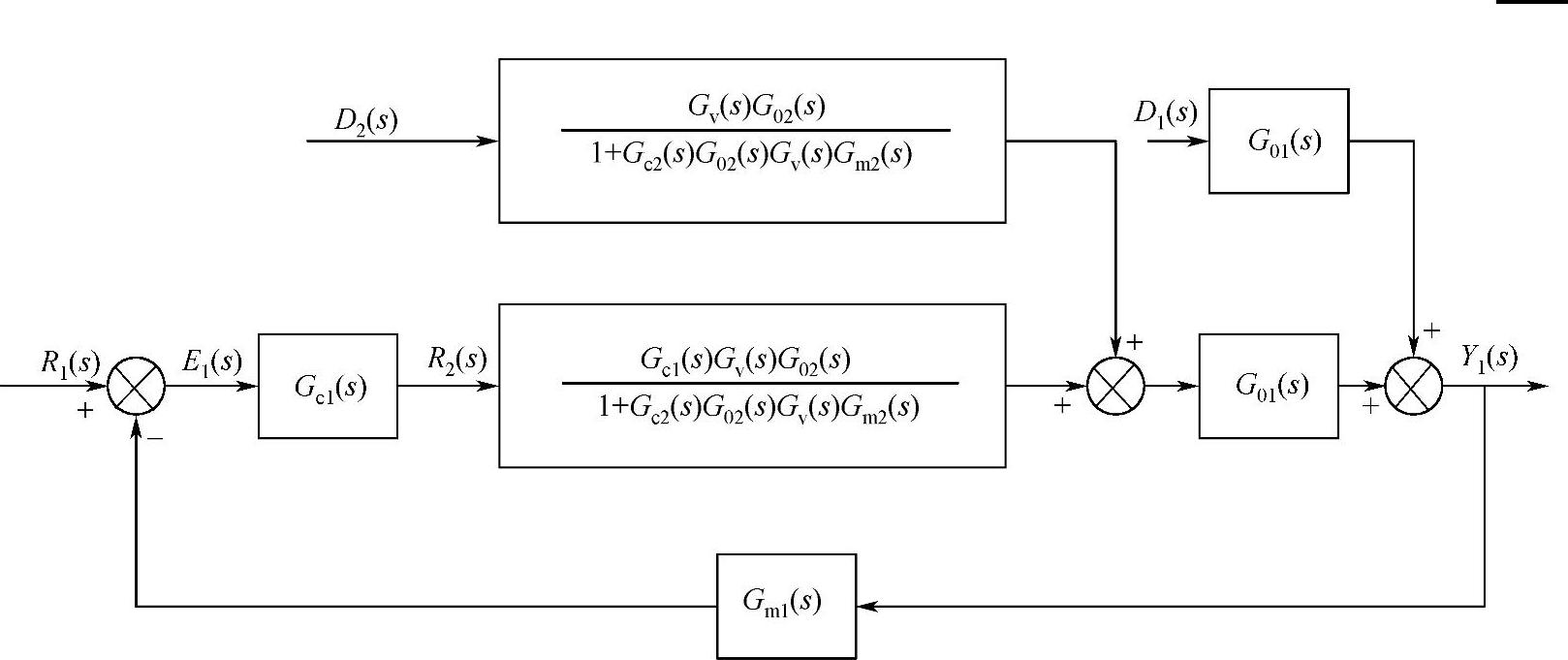
图5-16 串级系统等效框图

在串级控制系统中，若主、副控制器均采用比例作用，其比例放大系数分别为K_c1、K_c2，则式（5-6）可写为

这表明串级控制系统中，主、副控制器的比例放大系数的乘积越大，则系统的抗干扰能力越强，控制质量也就越高。

当干扰D₁由主回路作用于系统时（见图5-16），采用相同的分析可以得到串级控制系统对干扰D₁的抗干扰能力为

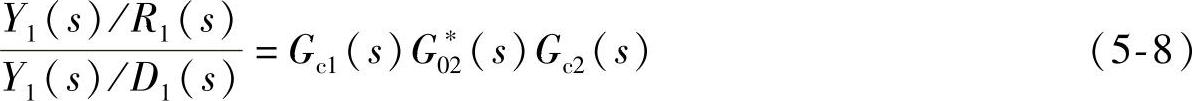
采用前面假设的主、副控制器，主、副被控对象及主、副变送器，则一次干扰作用于系统的抗干扰能力为

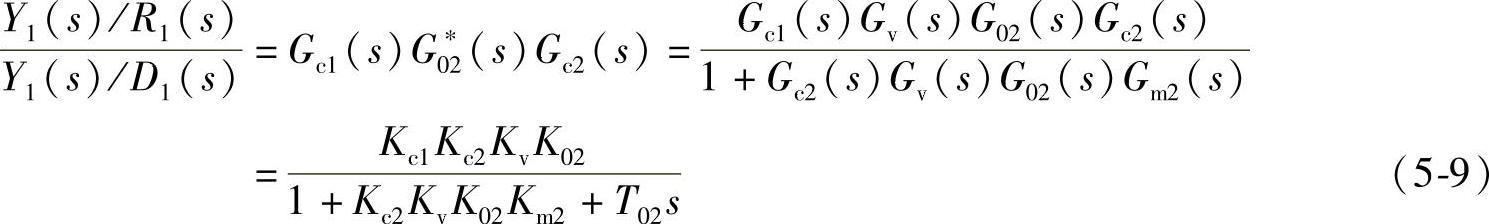
比较干扰由副回路进入系统时的抗干扰能力（见式（5-7））和干扰由主回路进入系统时的抗干扰能力（见式（5-9）），可得

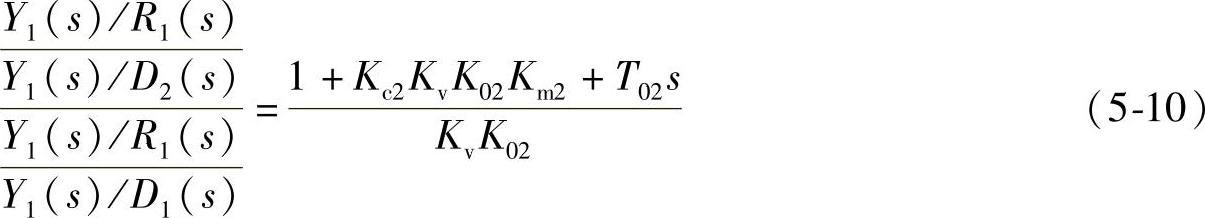
显然，式（5-10）是大于1的。也就是说，对串级控制系统，它对由副回路进入系统的干扰比由主回路进入系统的干扰有更强的抑制干扰的能力，并且在系统中其他环节特性不变的情况下，副控制器的放大系数越大，则抗干扰的能力越强。

对图5-13单回路控制时扰动D₂作用于副回路的结构框图如图5-17所示。

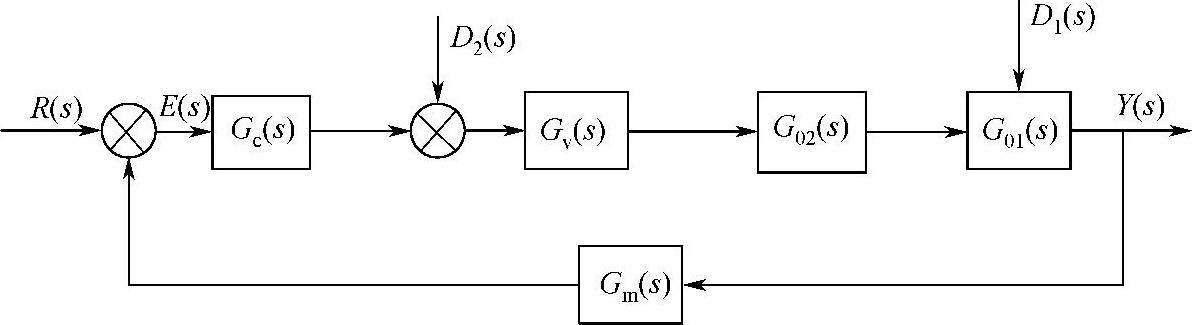
图5-17 单回路控制时扰动D₂作用于副回路的结构框图

单回路系统在扰动D₂和设定值作用下的传递函数分别为(www.xing528.com)

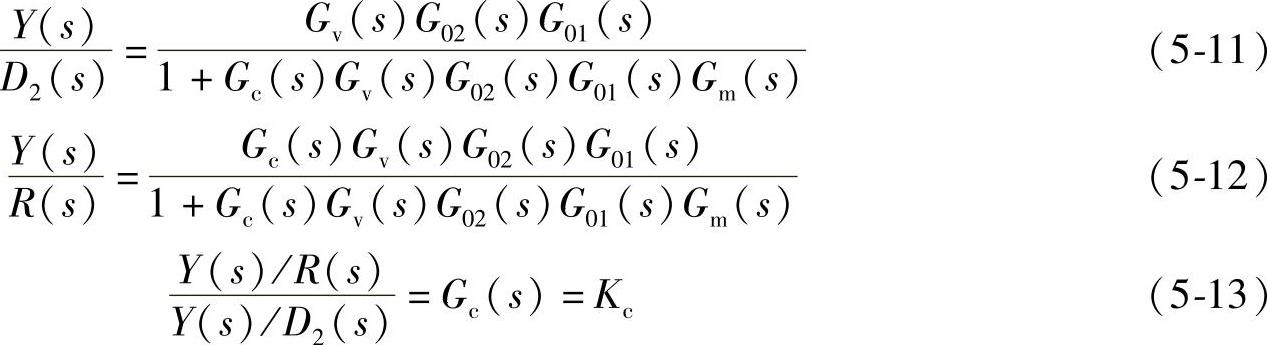
串级控制系统与单回路系统相比较，由于有副回路的存在，系统能迅速克服二次干扰对主被控变量的影响，大大提高了控制质量。同时，对于一次干扰，因等效时间常数的减小，其抗干扰能力也有一定提高。

5.2.1.3 串级控制提高了系统的工作频率

对于串级控制系统，可以把整个副回路看成主回路的一个环节，或把副回路看成等效被控对象G^∗₀₂（s）。G^∗₀₂（s）的传递函数为

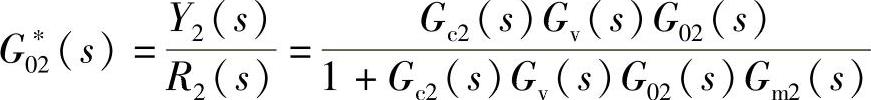
此时串级控制系统的特征方程为

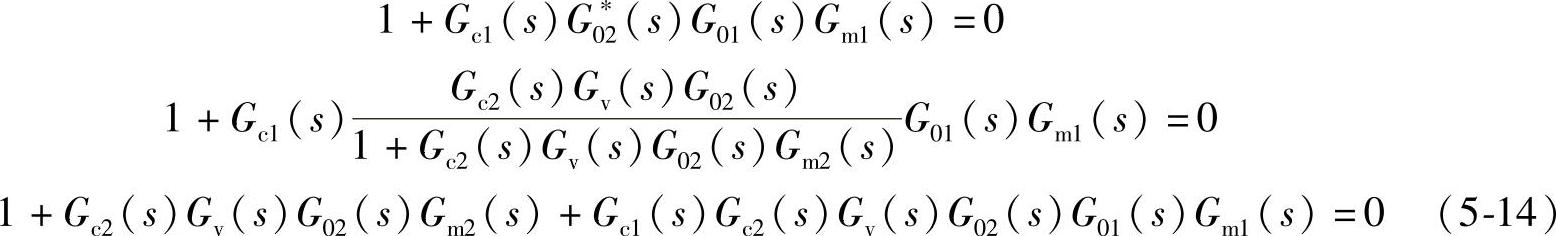
在主、副回路各环节的传递函数假设为

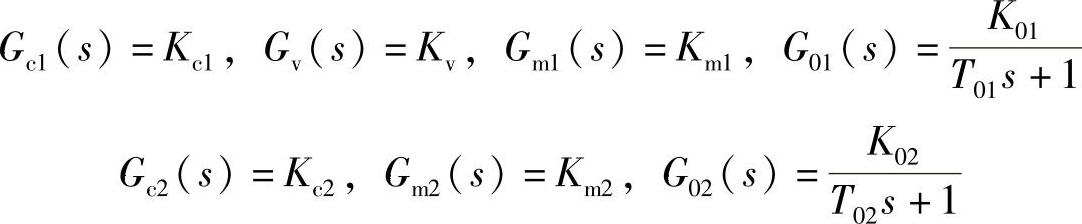
将其代入式（5-14），整理得串级控制系统的特征方程为

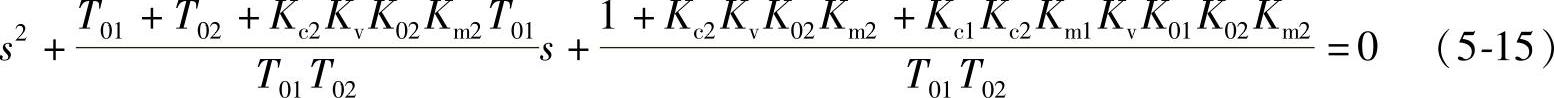
将其与典型二阶系统的标准型比较，有

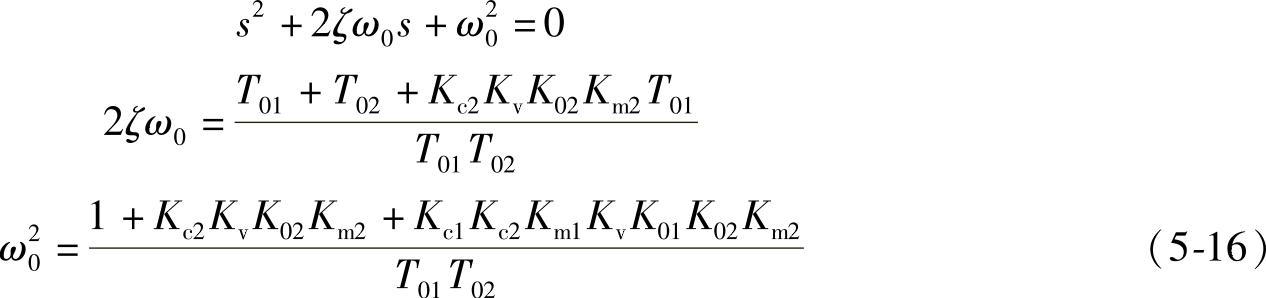
式中 ζ——串级控制系统的阻尼比；

ω₀——串级控制系统的无阻尼自然振荡角频率。

串级控制系统的工作角频率即其特征方程根的虚部为

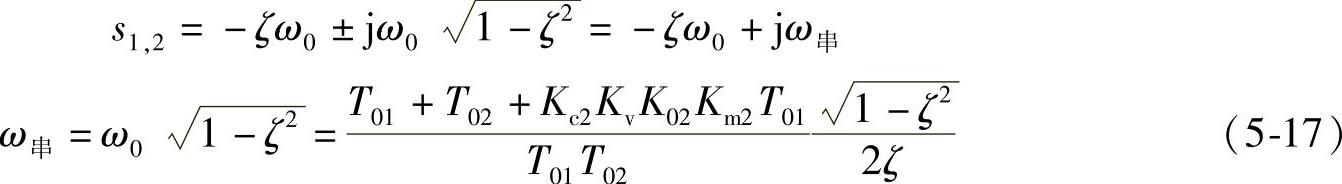
同理，可得单回路控制系统的特征方程及工作角频率为

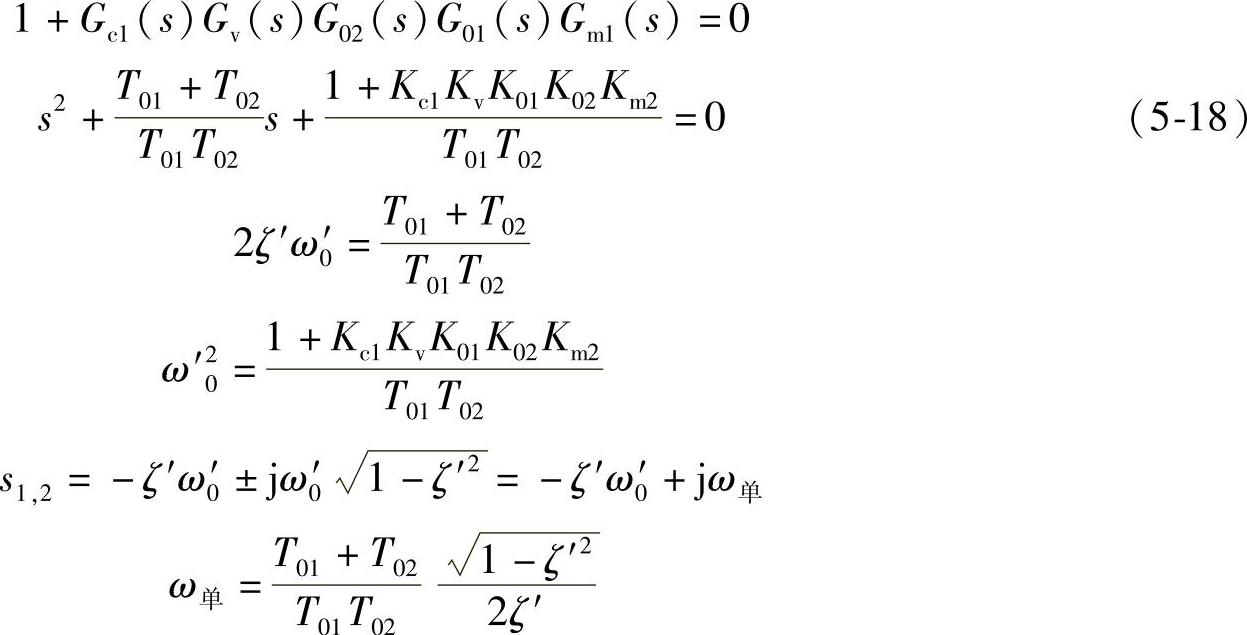
假设串级控制系统和单回路控制系统的衰减系数相同，即ζ＝ζ′，则

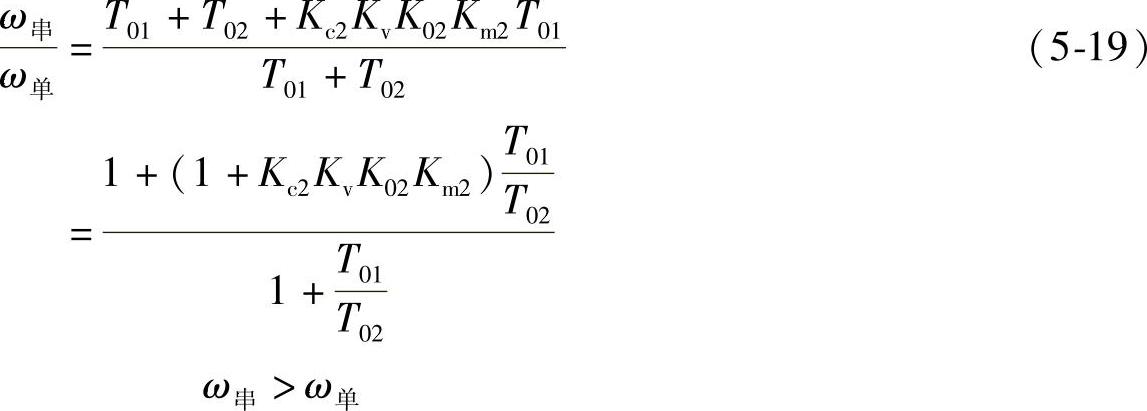
由此看到，当主、副被控对象均为一阶惯性环节，主、副控制器均为比例环节时，副回路的引入可以改善系统的动态特性，提高整个系统的工作频率，而且当主、副对象的特性一定时，副控制器的放大系数越大，系统的工作频率越高。当副控制器的放大系数一定时，系统的工作频率随主、副对象的时间常数的比值，即随T₀₁/T₀₂的增大而增大。串级控制系统的工作频率提高，使系统响应的振荡周期缩短，从而提高了系统的快速性，改善了系统的动态品质。

5.2.1.4 对负荷变化的适应性增强

单回路控制系统中，控制器参数是根据具体的被控对象特性整定得到的。一定的控制器参数只能适应于一定的对象特性，如果生产过程负荷变化，而且负荷的改变又会影响对象特性的变化时，原先整定好的控制器参数就不再能够适应，这时如果不及时修改控制器的参数，控制质量就会降低，这是单回路控制系统难以克服的矛盾。

对于串级控制系统，主回路是一个定值控制系统，副回路却是一个随动控制系统，且其设定值随主控制器的输出而变化。主控制器能够根据系统要求和负荷的变化不断修改副控制器的给定值，以适应设定值和负荷变化的情况。如果对象具有非线性特性，则可以把它设计在副回路之中。当负荷发生变化时，虽然副回路的衰减比会发生一些变化，稳定裕度会降低一些，但是它对主回路的稳定性影响却很小，串级控制系统对负荷变化的适应能力较强。

从串级控制系统的等效副对象的放大倍数K^∗₀₂（s）来看，即

当负荷变化时，将会引起副对象特性G₀₂（s）的变化，但是在一定的条件（K_c2K_vK₀₂K_m2＞1）下，对等效副对象的放大倍数K₀∗₂的影响却很小。这样对主回路的影响也就很小。当副控制器的放大系数K_c2整定得足够大时，则有K_c2K_vK₀₂K_m2＞＞1，K₀∗₂可近似为

对于串级控制系统，当副控制器的放大系数整定得足够大时，副被控对象的等效放大倍数仅仅与检测变送环节的增益K_m2有关，而与控制阀和副被控对象的增益K₀₂（s）无关。这表明串级控制系统能自动克服对象特性的影响，从而显示它对负荷变化具有一定的自适应能力。

5.2.1.5 串级控制可实现更为灵活的控制操作方式

串级控制系统可实现串级控制、主控制和副控制多种控制方式。主控制是切除副回路，以主被控变量作为被控变量的单回路控制；副控制是切除主回路，以副被控变量构成的单回路控制。若系统中某些部件发生故障，则系统可灵活地切换，减小对生产过程的影响。

为了对串级控制系统的控制效果有一个定量的概念，下面采用计算机辅助设计给出一个例子。

例如设串级控制系统的框图如图5-18a所示，Simulink仿真图如图5-18b所示，其中主、副被控对象的传递函数分别设为

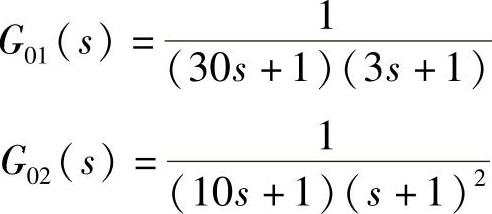
主、副控制器的传递函数分别采用PI和P控制，其传递函数为

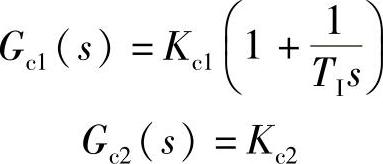
对于单回路控制系统，取K_c＝3.7，T_I＝38，对于串级控制系统，控制器参数选取K_c1＝8.4，K_c2＝10，T_I＝12.8。单回路系统和串级控制系统的阶跃响应如图5-19所示，单回路系统和串级控制系统在二次干扰作用下的响应曲线如图5-20所示，单回路系统和串级控制系统在一次干扰作用下的响应曲线如图5-21所示，单回路系统和串级控制系统在一次干扰和二次干扰同时作用下的响应曲线如图5-22所示。

从系统的响应曲线估算得系统的各项指标见表5-1。

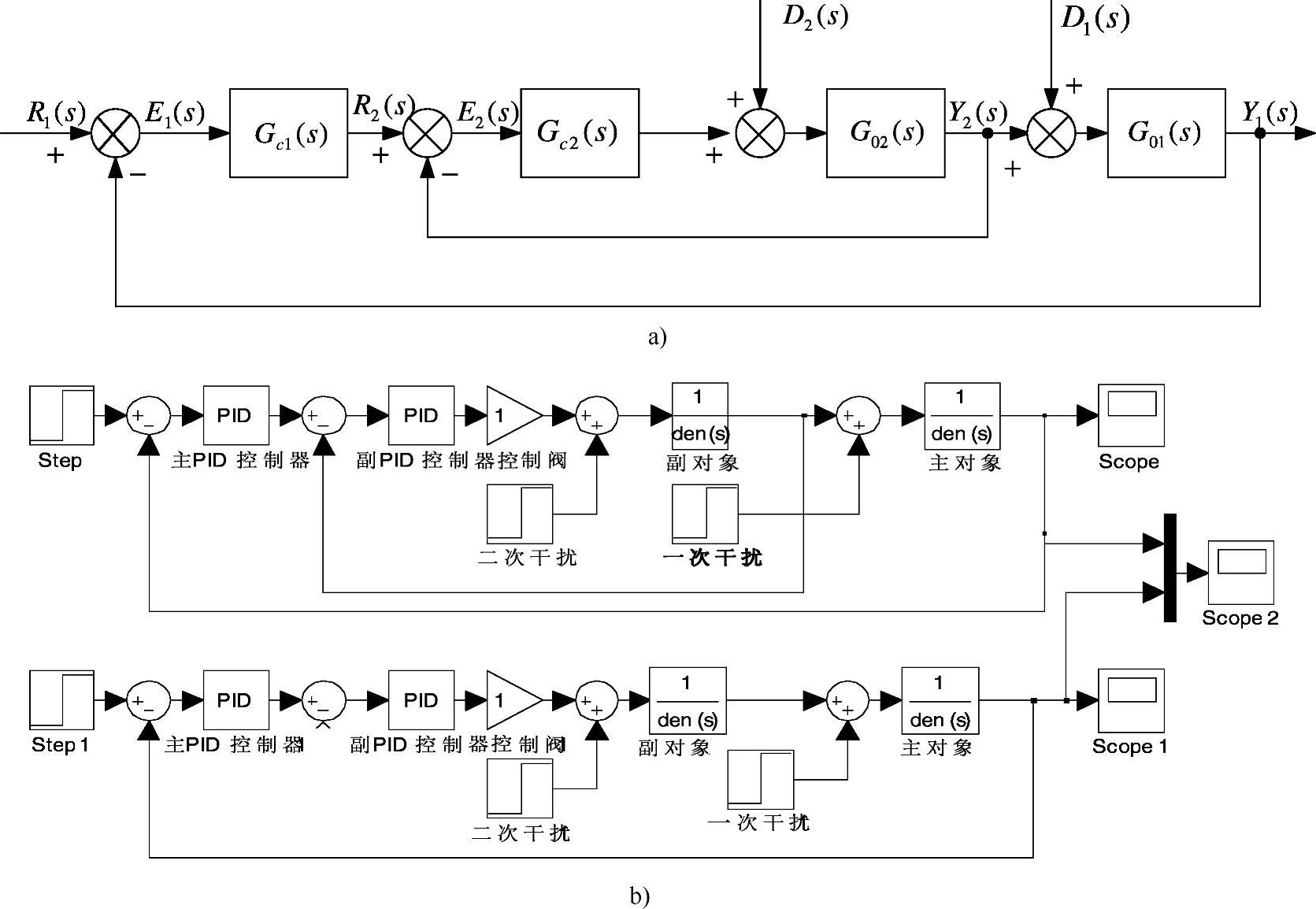
图5-18 串级控制系统框图及Simulink仿真图

a）框图 b）Simulink仿真图

表5-1 单回路控制与串级控制效果

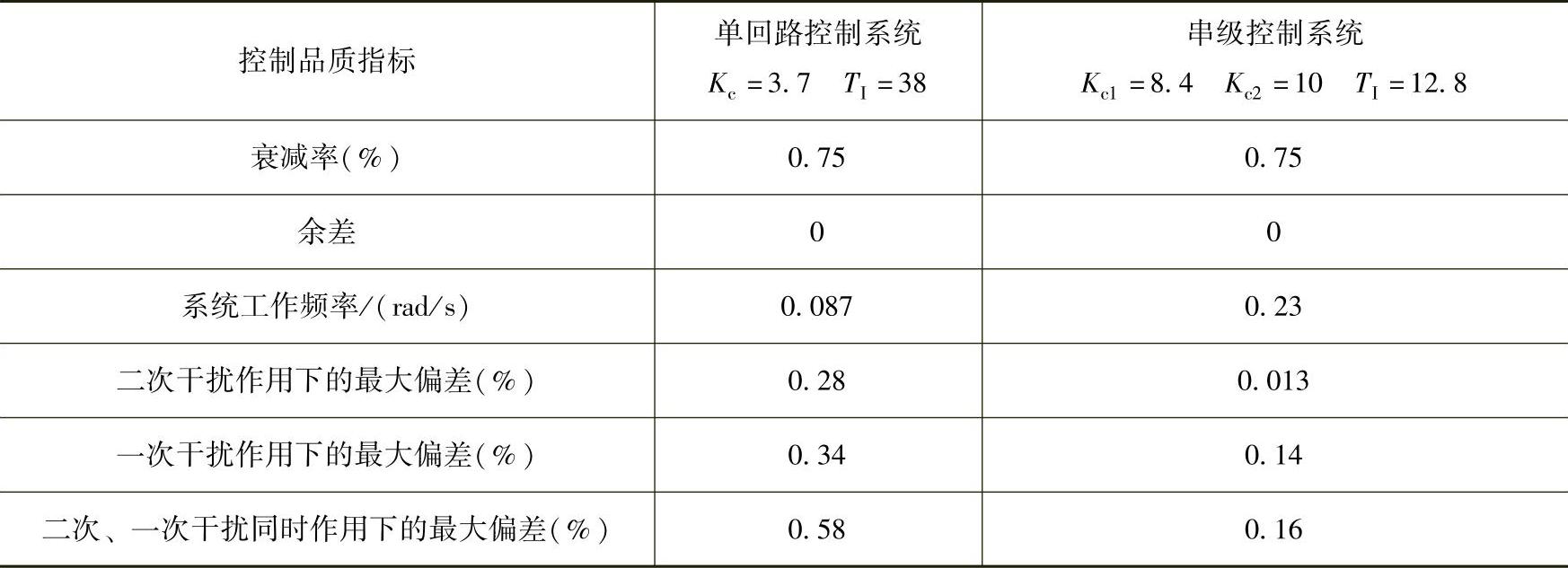
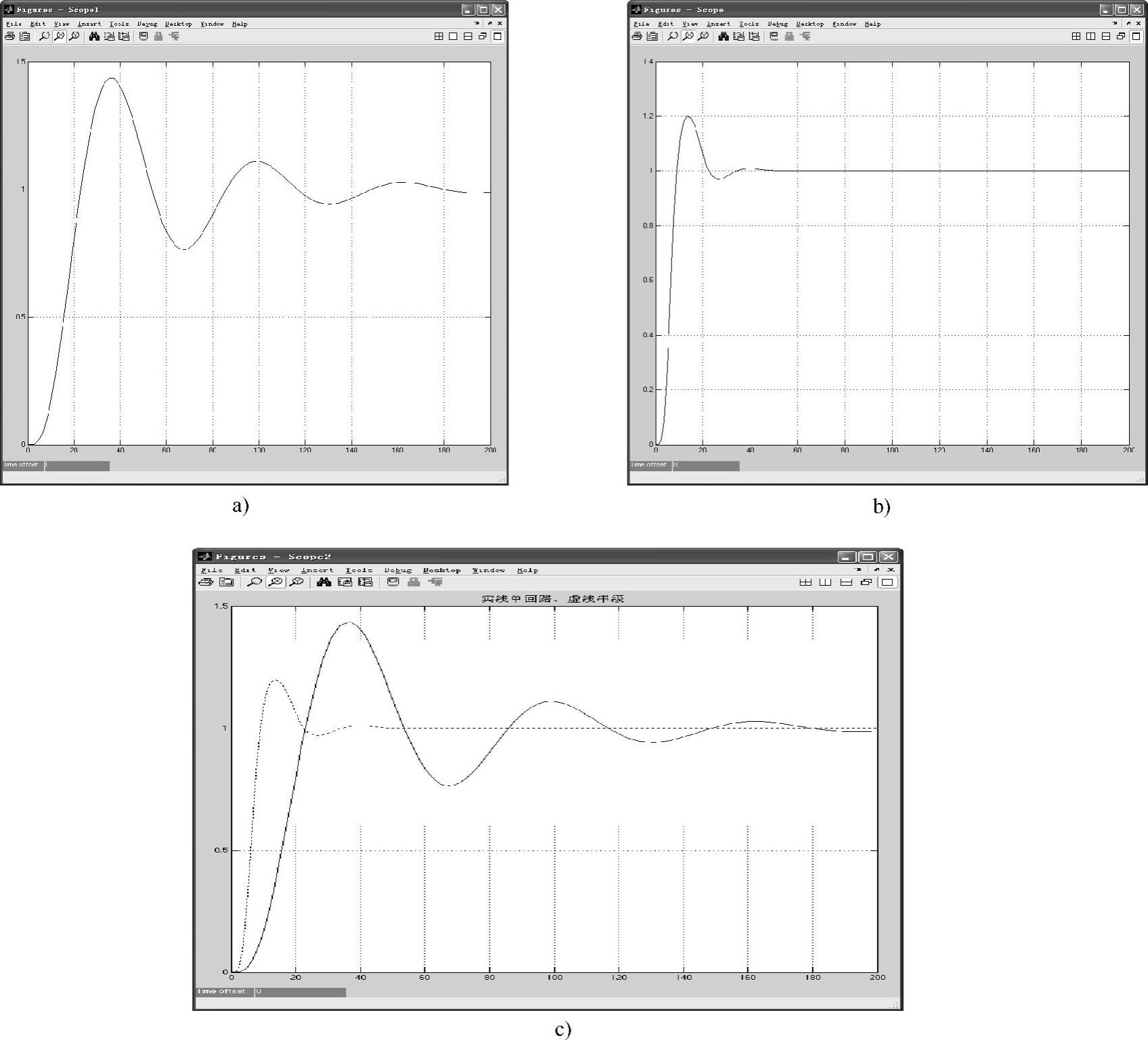
图5-19 单回路系统和串级控制系统单位阶跃响应

a）单回路系统 b）串级控制系统 c）单回路、串级控制比较

从表5-1中可以定量地看出，采用串级控制，系统的工作频率大大提高；一次干扰和二次干扰作用下系统的最大动态偏差大大减小，串级控制系统对控制品质的改善是十分明显的。