被控对象动态特性分析

过程控制的被控对象涉及的范围很广。被控对象不一定是指一个具体的设备，不少情况下被控对象是指一个过程。有些过程可能涉及好几种设备，而在有些设备内部可能包括了几个过程。

过程控制被控对象的内在机理较为复杂，有简单过程、有存在严重非线性的过程、有多变量过程、有被控对象的特性随时间或工作条件而变化等。对被控对象动态特性的了解，一种方法是通过分析被控对象的工作机理，建立被控对象的数学模型。但由于连续生产过程的复杂性，完全从机理上揭示其内在规律，获得精确的数学模型还有较大的困难。另一种方法是工程上经常使用的方法，它采用实验法来获得被控对象的数学模型。这种方法通过测量被控对象的阶跃响应曲线（称为飞升曲线）近似确定被控对象的数学模型。

过程控制中大多数被控对象都具有较大的惯性和时间延迟，一般不具有振荡特性，其飞升曲线是单调变化的。按照被控对象所含存储器件的多少，被控对象可分为单容对象、双容对象和多容对象。按照被控变量受扰动作用后的变化规律，被控对象可分为有自平衡能力的对象和无自平衡能力的对象。典型被控对象的动态特性大致可分为：

1.自平衡能力的过程

系统的被控变量受到扰动作用后，偏离了原来的平衡状态，在没有外部干预的情况下（指没有自动控制或人工控制参与），被控变量依靠被控对象内部的反馈机理，能自发达到新的平衡状态，这种特性称自平衡，具有这种特性的过程称为自平衡能力的被控过程。

（1）自平衡的非振荡过程

对于具有自平衡能力的被控对象，若在外部阶跃信号作用下系统的原有平衡状态被破坏，系统在外部信号作用下的输出响应单调的从一个稳态趋向于另一个稳态，该类过程被称为具有自平衡的非振荡过程。

例如，液位贮罐在进料阀开度增大时，原来的液位会上升，由于出料阀开度未变，随着液位的升高，静压增大，出料量也增大，因此液位上升逐渐变慢，直到液位达到一个新的平衡状态，如图4-3a、b所示，多容液位自平衡非振荡过程如图4-3c、d所示。

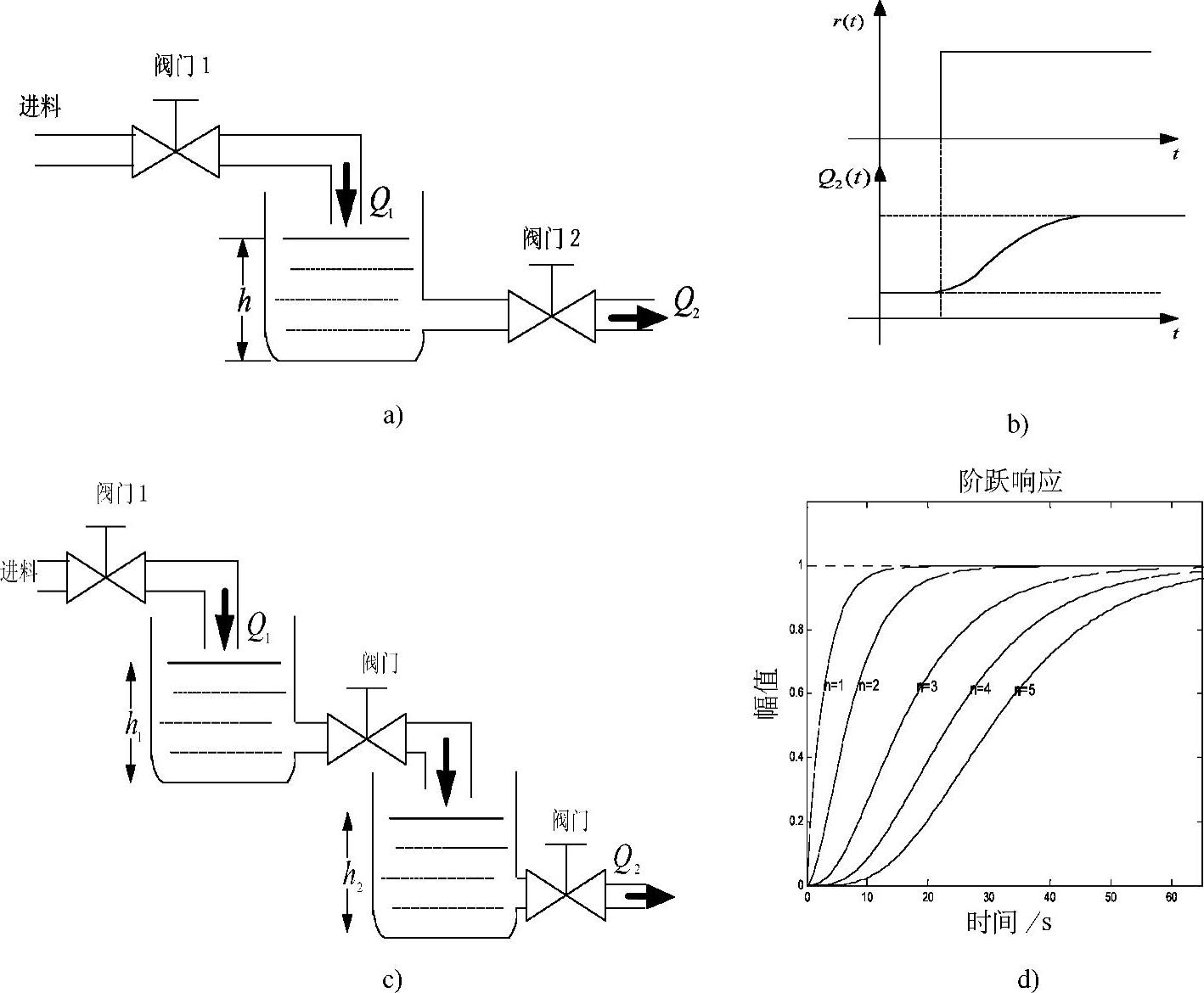
图4-3 自平衡非振荡过程的阶跃响应

a）单容液位贮罐原理图 b）动态过程响应 c）多容液位贮罐原理图 d）动态过程响应

具有自平衡非振荡过程特性的单容、双容及多容被控对象的传递函数可用一阶惯性环节、一阶惯性加时滞环节、二阶非振荡环节、二阶非振荡加时滞环节和高阶环节描述，见式（4-1）。

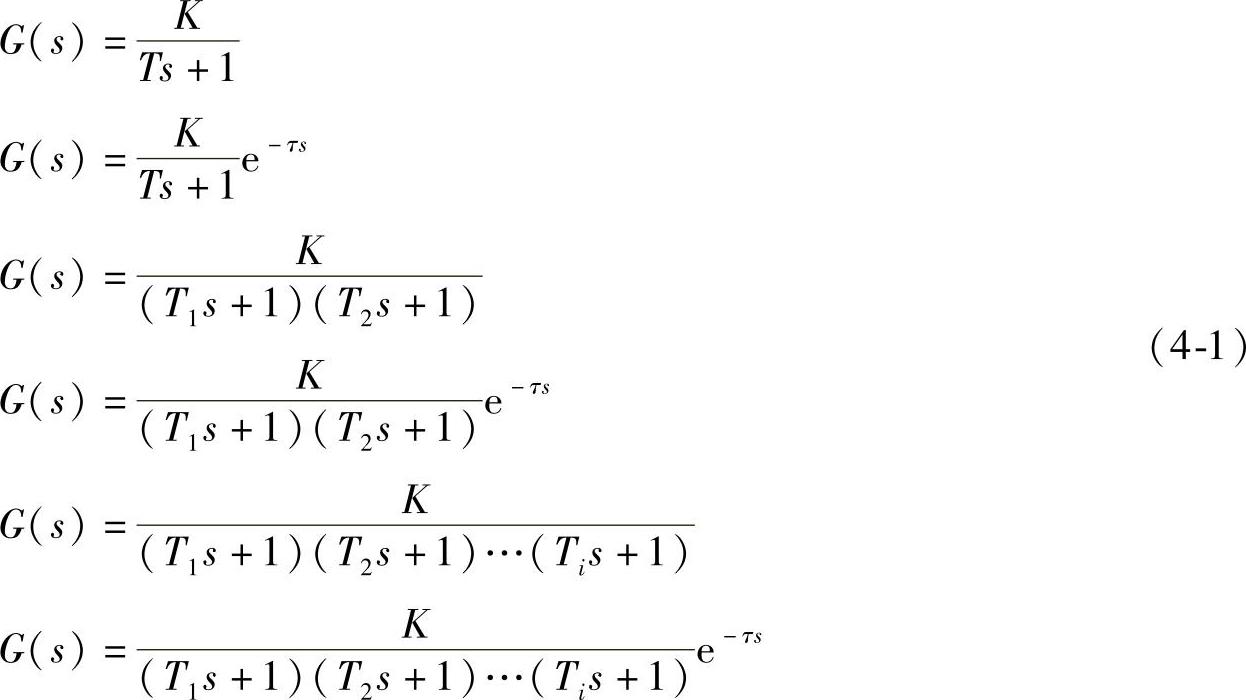
从响应曲线来看，n＝1为单容对象的阶跃响应曲线，其响应曲线的切线斜率最大，以后随时间增大逐渐减小到零，曲线在动态的初始阶段变化最快，以后逐渐变慢。从n≥2开始的双容和多容被控对象的阶跃响应曲线与n＝1时的曲线有明显的不同。双容被控对象和多容被控对象在t＝0时，阶跃响应曲线的斜率是零，随时间变化，斜率逐渐变大，达到某一个最大值时，又开始逐渐减小，直到减小到零。曲线在斜率最大处有一个拐点。双容对象和多容对象在动态过程的初始阶段变化非常缓慢，在动态过程的中间阶段变化较快，但其变化速度仍不及单容对象，且容量元件越多，变化速度越慢。所以，多容对象表现出的特点就是惯性大，响应慢。

在工业控制过程中，常根据被控对象的实验曲线来近似拟合被控对象的传递函数为一阶惯性加滞后的形式，即

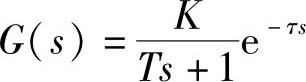
被控对象有三个参数，即时间常数T，放大系数K和容量延迟（时滞）τ。

（2）自平衡的振荡过程

过程系统具有自平衡能力，系统在外部阶跃信号作用下，输出响应为衰减振荡特性，系统的过渡过程最终趋于新的稳态值。系统的阶跃响应曲线如图4-4所示，其传递函数可表示为

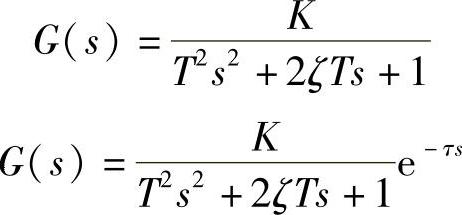
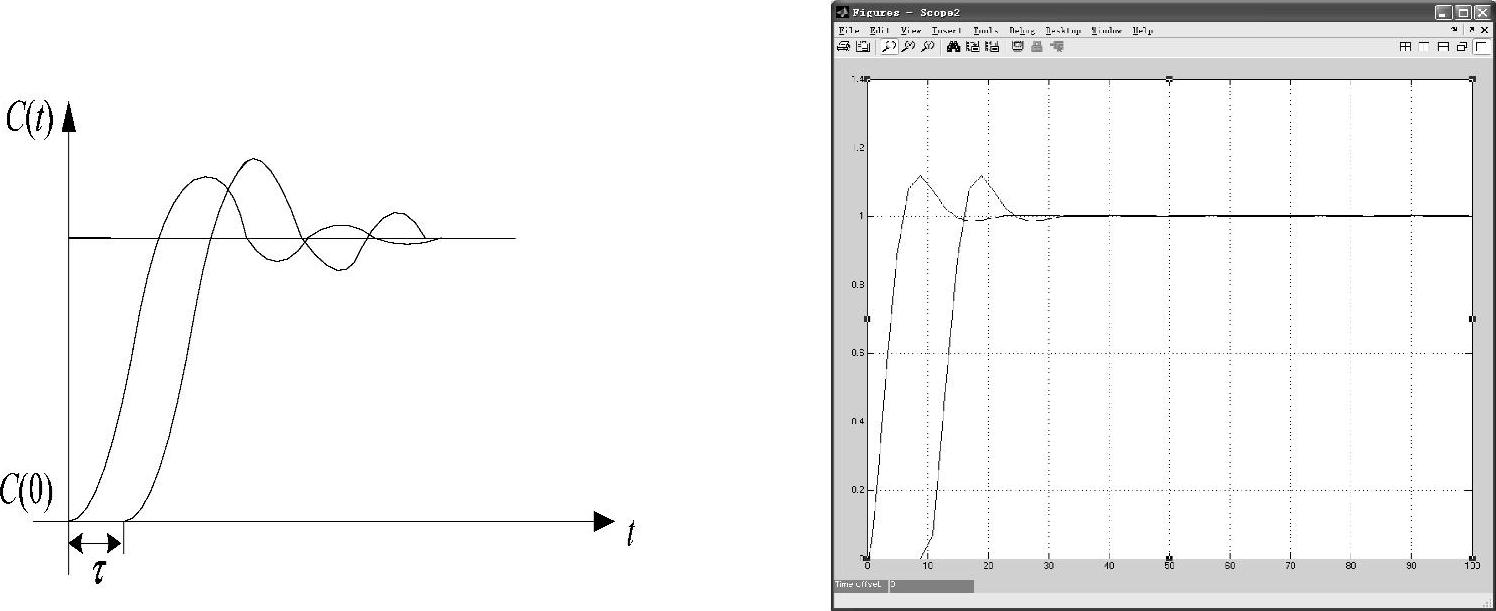
图4-4 自平衡振荡系统的阶跃响应曲线

2.无自平衡能力的过程

当被控对象原来的平衡状态被扰动作用破坏后，如果不依靠自动控制或人工控制的外来作用，被控变量将一直变化下去，不可能达到新的平衡状态，称这类对象为无自平衡能力的被控对象（被控过程）。

对于无自平衡能力的过程，若在外部阶跃信号作用下系统的原有平衡状态被破坏，系统在外部信号作用下的输出响应无振荡地从一个稳态一直上升或下降，不能趋向于新的稳态，该类过程称为无自平衡的非振荡过程。图4-5所示为单容无自平衡液位系统原理图和系统阶跃响应。

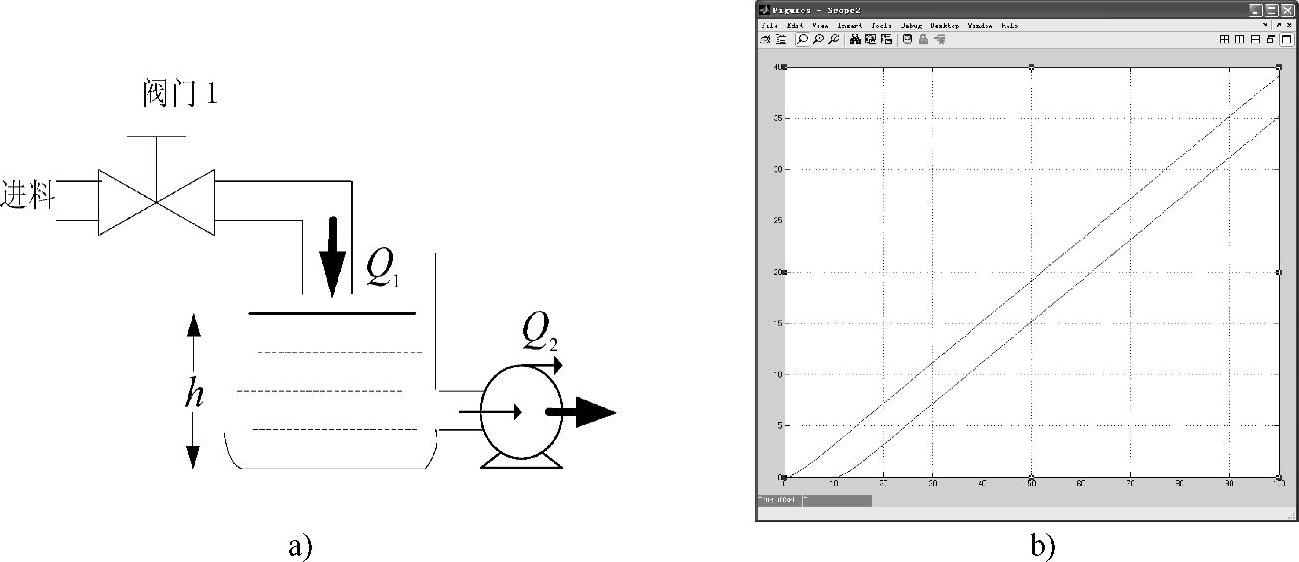
图4-5 无自平衡非振荡系统的阶跃响应

a）单容无自平衡液位系统 b）系统阶跃响应

无自平衡的非振荡系统的数学模型为

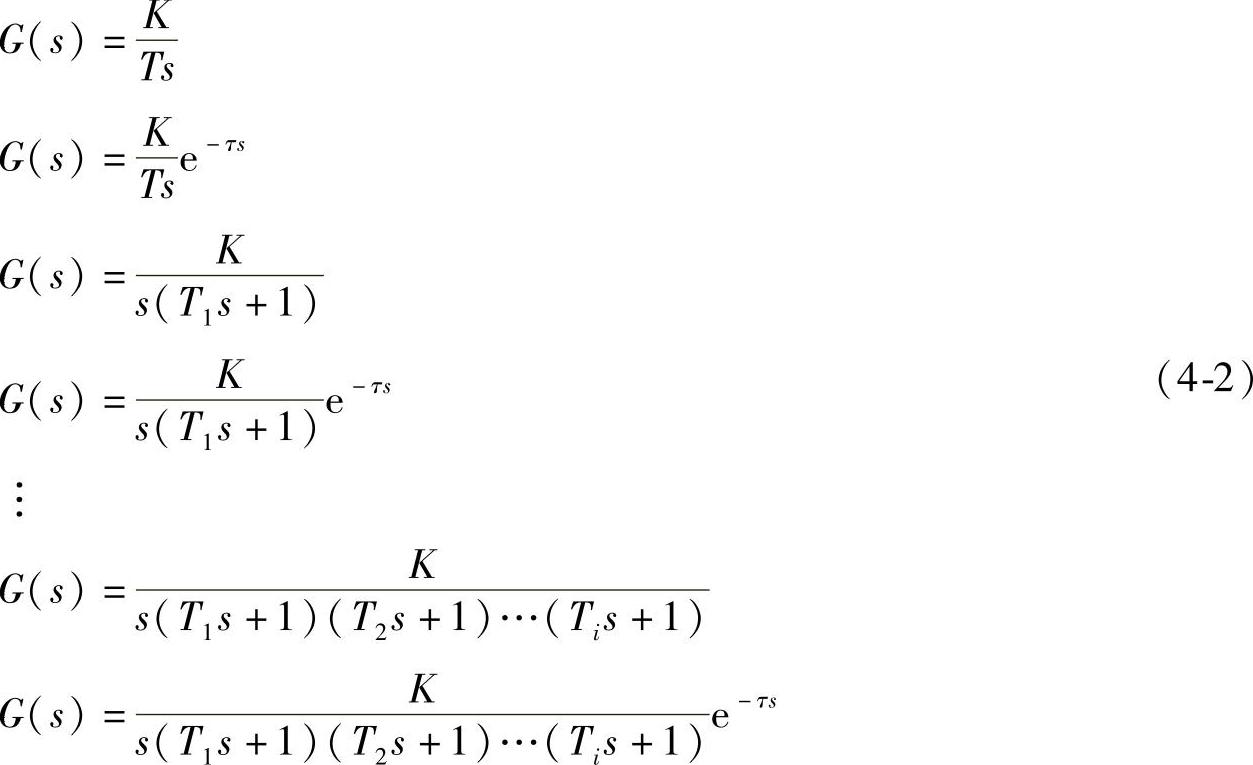
3.具有反向特性的过程

该类过程在阶跃输入信号作用下，系统的输出先降后升，即响应曲线在开始与结束时出现反向的变化，故称该过程具有反向特性，其阶跃响应曲线如图4-6所示。

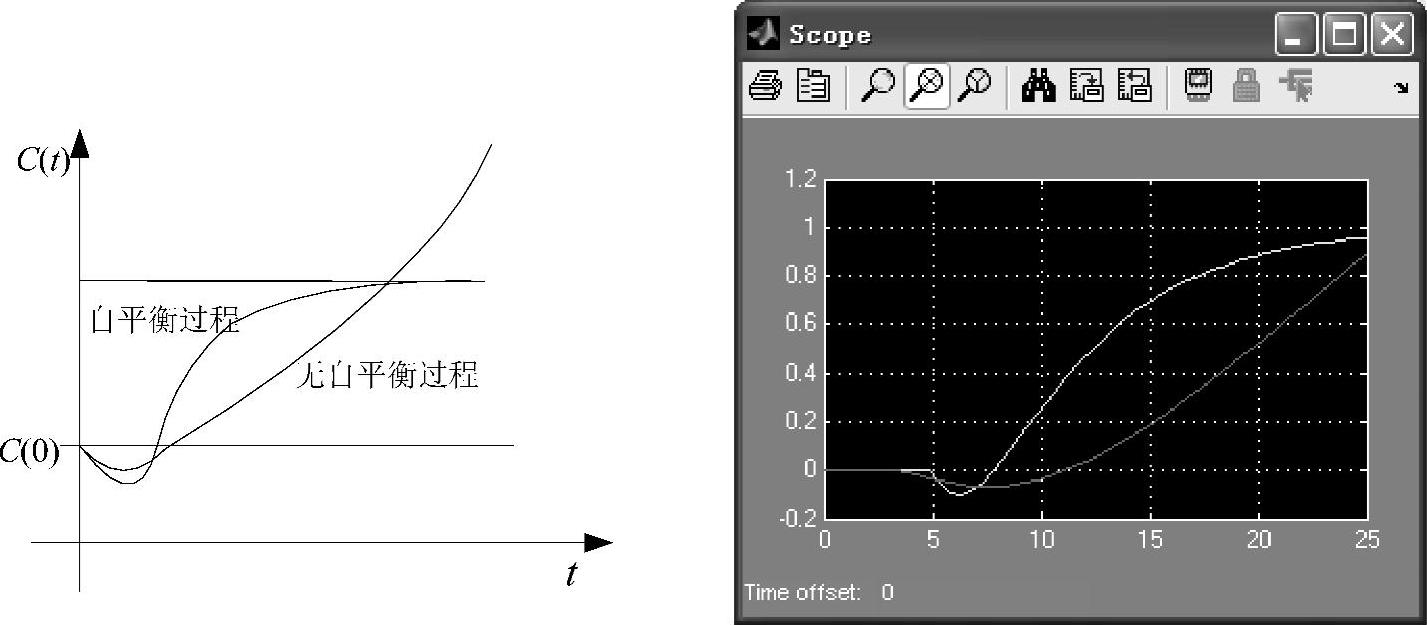
图4-6 反向特性系统的阶跃响应曲线

具有反向特性过程的传递函数为

自平衡型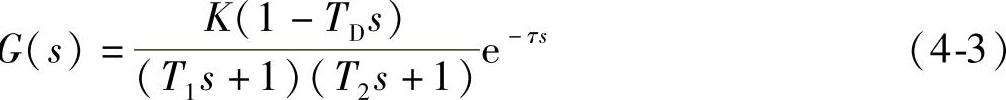

无自平衡型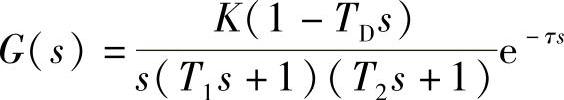

对于锅炉锅筒水位系统就是一个典型的反向特性过程，当蒸汽用量阶跃变化时，引起蒸汽压力突然下降，锅筒水位因水的急速变化造成系统虚假水位上升，但因用汽量的增加，最终水位反而下降。

对于具有反向特性的过程，其传递函数总有一个右零点，系统属于非最小相位系统，其控制较难，需要特殊处理。

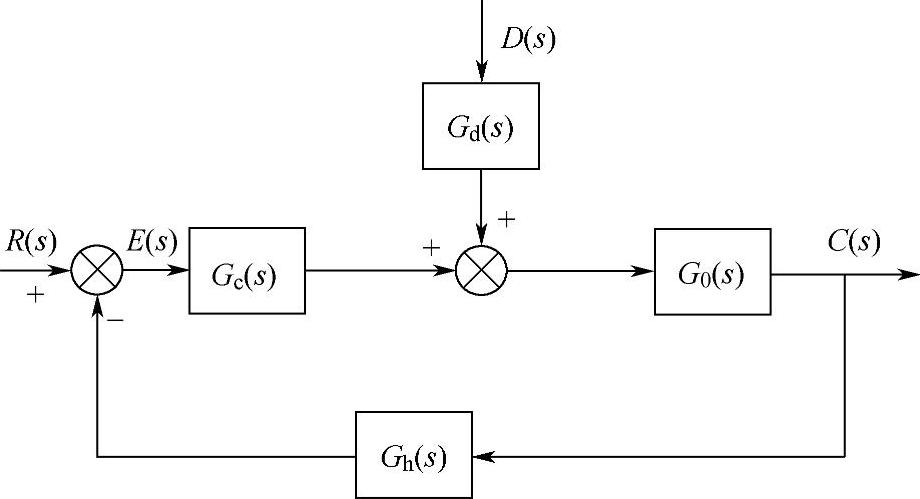
图4-7 给定值输入和扰动输入系统的框图

工业过程除上述几种类型外，有些控制过程还存在严重的非线性、时变，甚至不稳定。如何使控制作用有效地克服干扰对被控变量的影响，关键要研究对象特性、研究各种输入量对被控对象的影响、研究控制变量的选取等。

（1）被控对象特性对控制系统性能的影响

典型给定值输入（设定值）和扰动信号输入下系统的框图如图4-7所示。控制系统的输出可由两条通道来产生：

控制通道——设定值对被控变量影响的通道，其作用是抵消扰动影响，以使被控变量尽可能快地维持在给定值附近。系统在设定值单独作用下产生的输出为

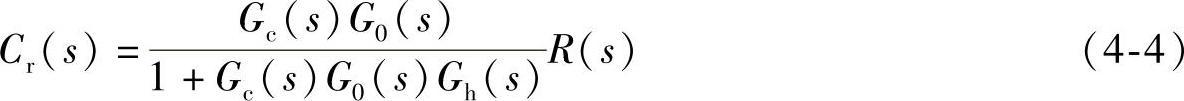
干扰通道——干扰信号对被控变量影响的通道，扰动信号单独作用下系统的输出为

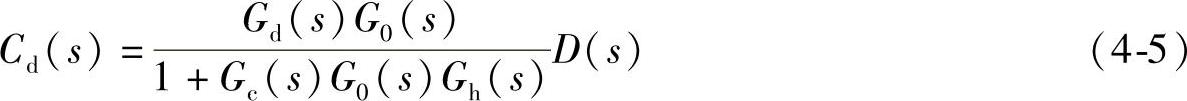
为分析方便起见，假设各个环节的传递函数如下：

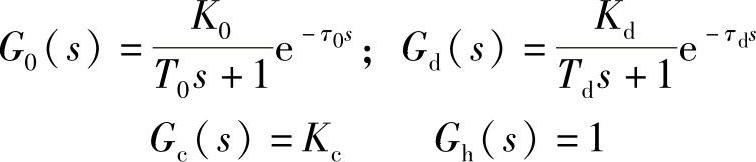
（2）控制通道增益对系统性能的影响

过程控制系统中假设扰动信号为零d（t）＝0，设定值信号为单位阶跃信号r（t）＝1（t）作用下，系统的稳态输出及稳态误差为

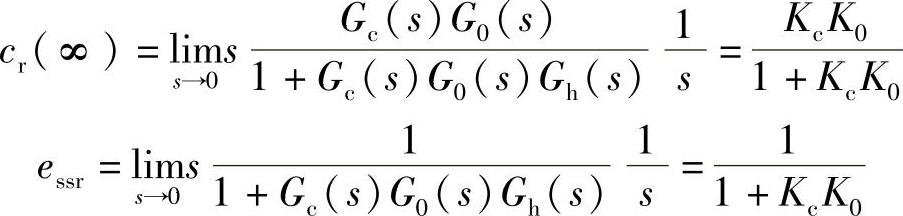
可见，随着控制通道增益K_c的增加，系统的稳态误差减小且控制作用增强，但系统的稳定性变差。

假设被控对象的传递函数为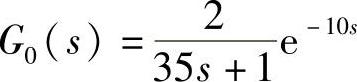，系统在单位阶跃信号作用下，不同控制通道增益下系统的响应曲线如图4-8所示。

(www.xing528.com)

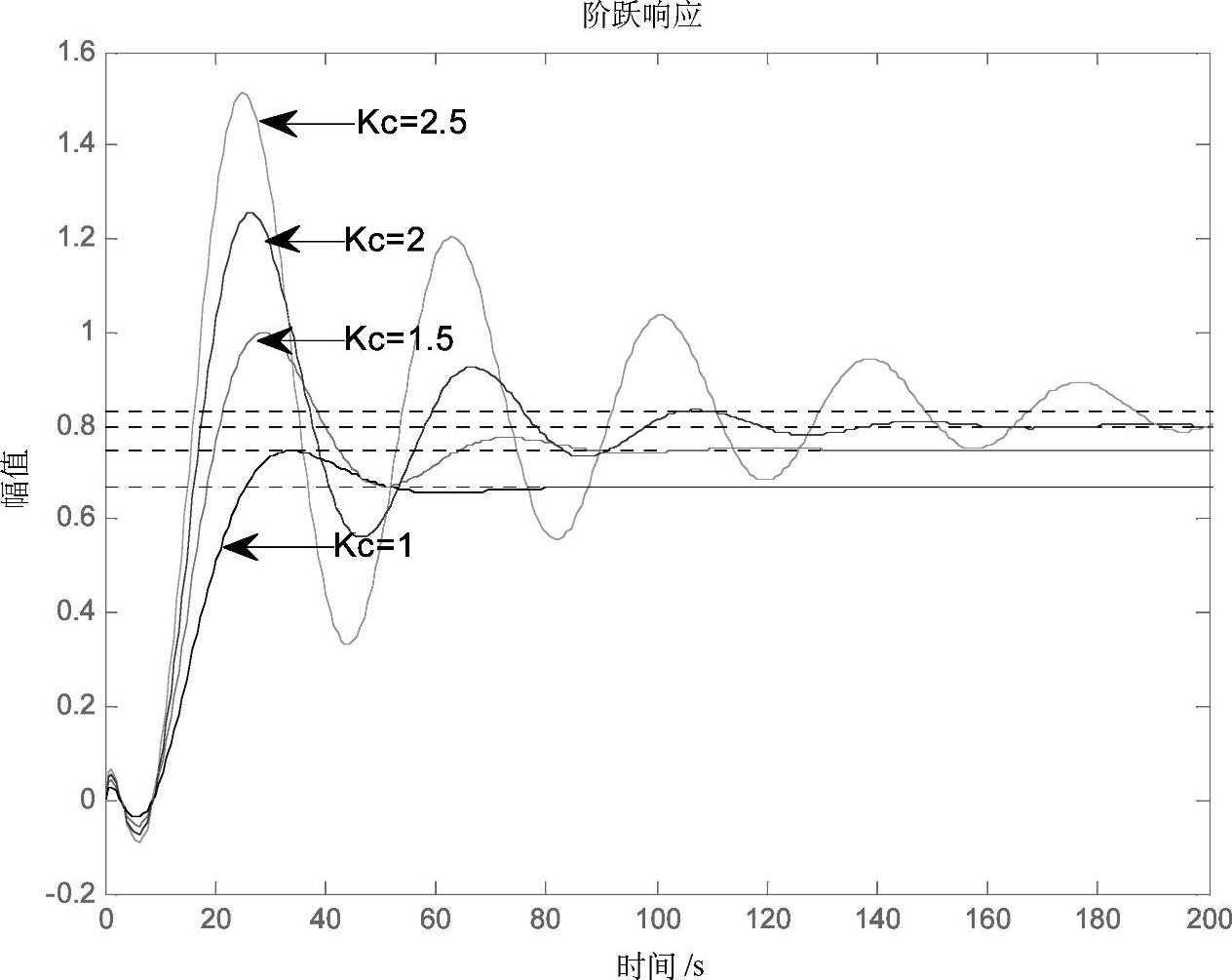
图4-8 不同过程增益下系统的阶跃响应曲线

由于增益反映的是对象处于稳态下输出与输入之间的关系，所以增益是描述对象静态特性的参数。并且控制器的增益应随被控对象的增益发生变化，以保证闭环系统有足够的稳定裕量和足够快地克服系统的稳态误差。

（3）扰动通道增益对系统性能的影响

过程控制系统中假设设定值为零r（t）＝0，设扰动信号在d（t）＝1（t）的作用下，系统的稳态输出及稳态误差为

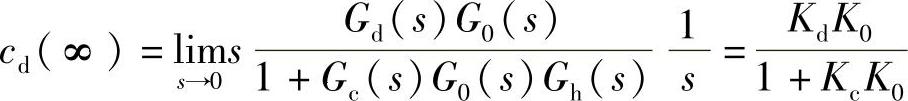
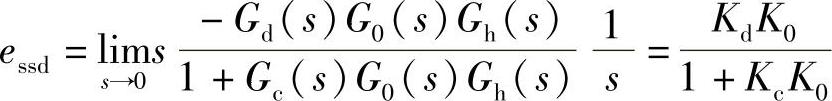
可见，随着扰动通道增益K_d的增加，系统的稳态误差增加，且扰动作用下的输出响应也增大。

假设系统的传递函数为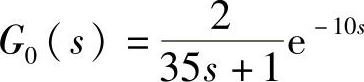、、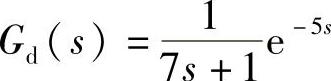G_h（s）＝1，则系统在单位阶跃扰动信号的作用下，不同扰动通道增益变化的响应曲线如图4-9所示。

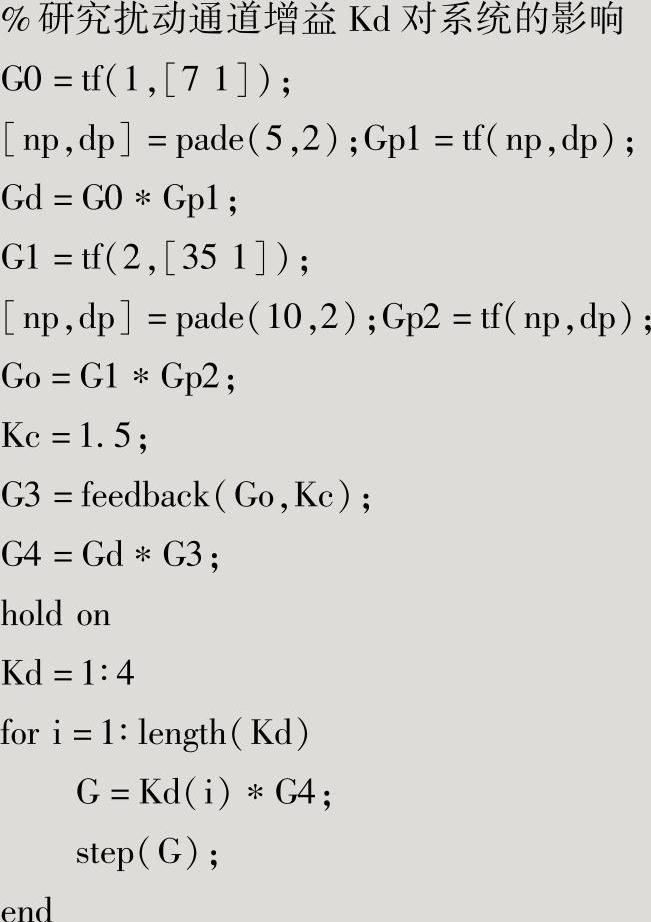
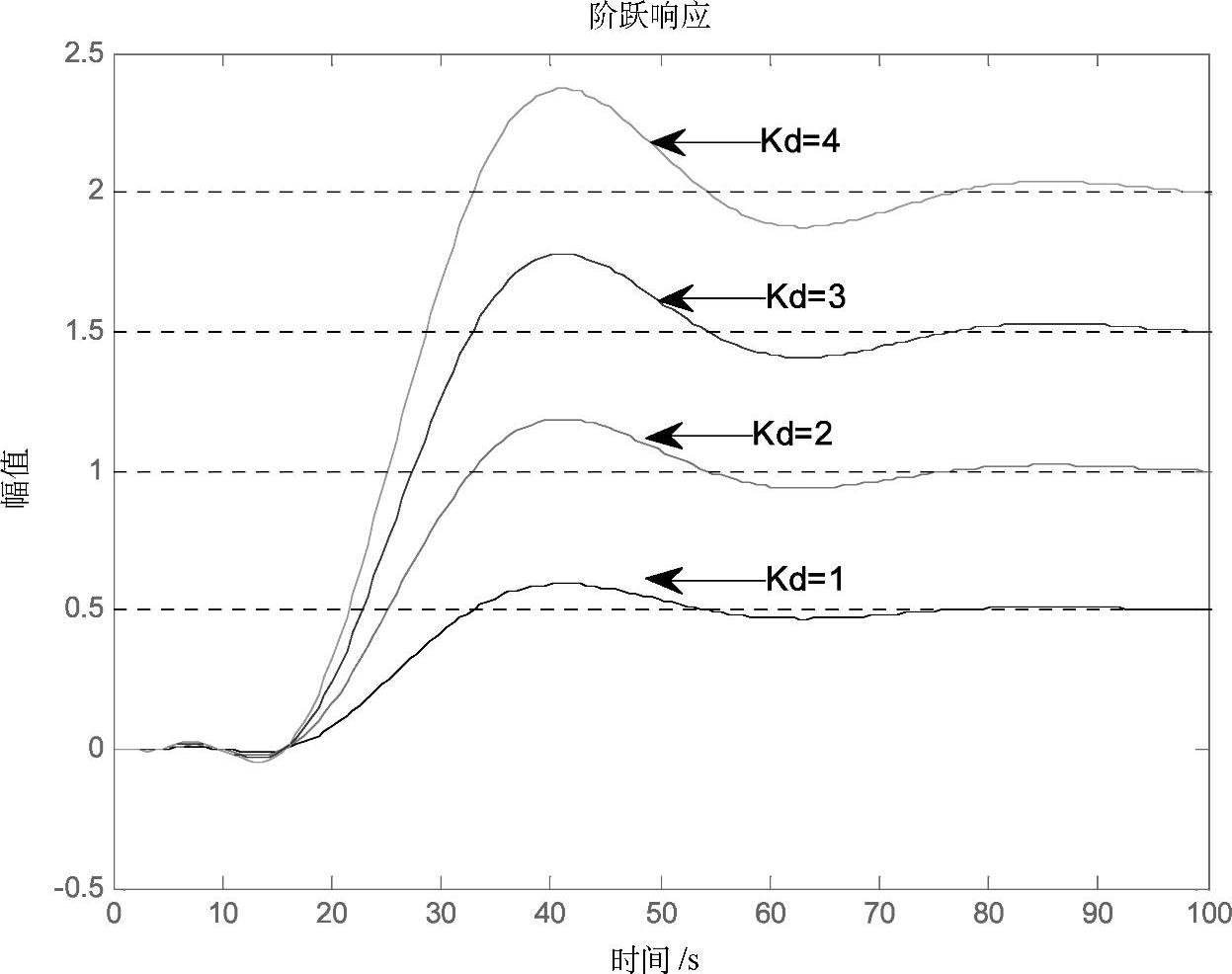
图4-9 不同过程扰动增益下系统的阶跃响应曲线

（4）控制通道时间常数的影响

控制通道时间常数T是指当被控对象受到阶跃输入信号作用后，被控量以初始速度变化，达到新的稳态值所需要的时间。时间常数T是因为物料或能量的传递需要通过一定的阻力而引起的，反映被控变量的变化快慢，因此T是对象的一个动态参数。

对图4-6所示的控制系统，系统的特征方程为

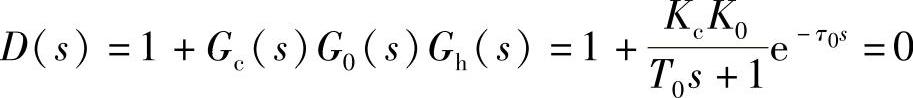
对应的相频特性为

φ（ω）＝-ωτ₀-arctanT₀ω

相位剪切频率条件为

-ω_cτ₀-arctan T₀ω_c＝-π

产生的相角裕量为

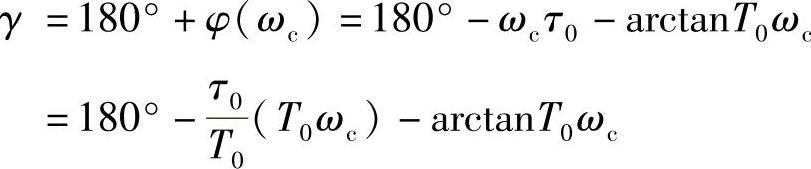
若τ₀/T₀固定，则相位剪切频率条件T₀ω_c不变，对系统的相角裕量也没有影响；若τ₀/T₀固定，且时间常数T₀增大，则为使系统的相角裕量不变，应使ω_c减小，即系统的振荡频率减小，系统的动态响应拖长，过渡过程时间加大；若τ₀/T₀固定，且时间常数T₀减小，则为使系统的相角裕量不变，应使ω_c增大，即系统的振荡频率增大，系统的动态响应加快，过渡过程时间缩短。

控制通道时间常数越小，系统的动态响应越快、工作频率上升、系统的过渡过程时间越短，能迅速反映控制效果，提高系统的控制质量。

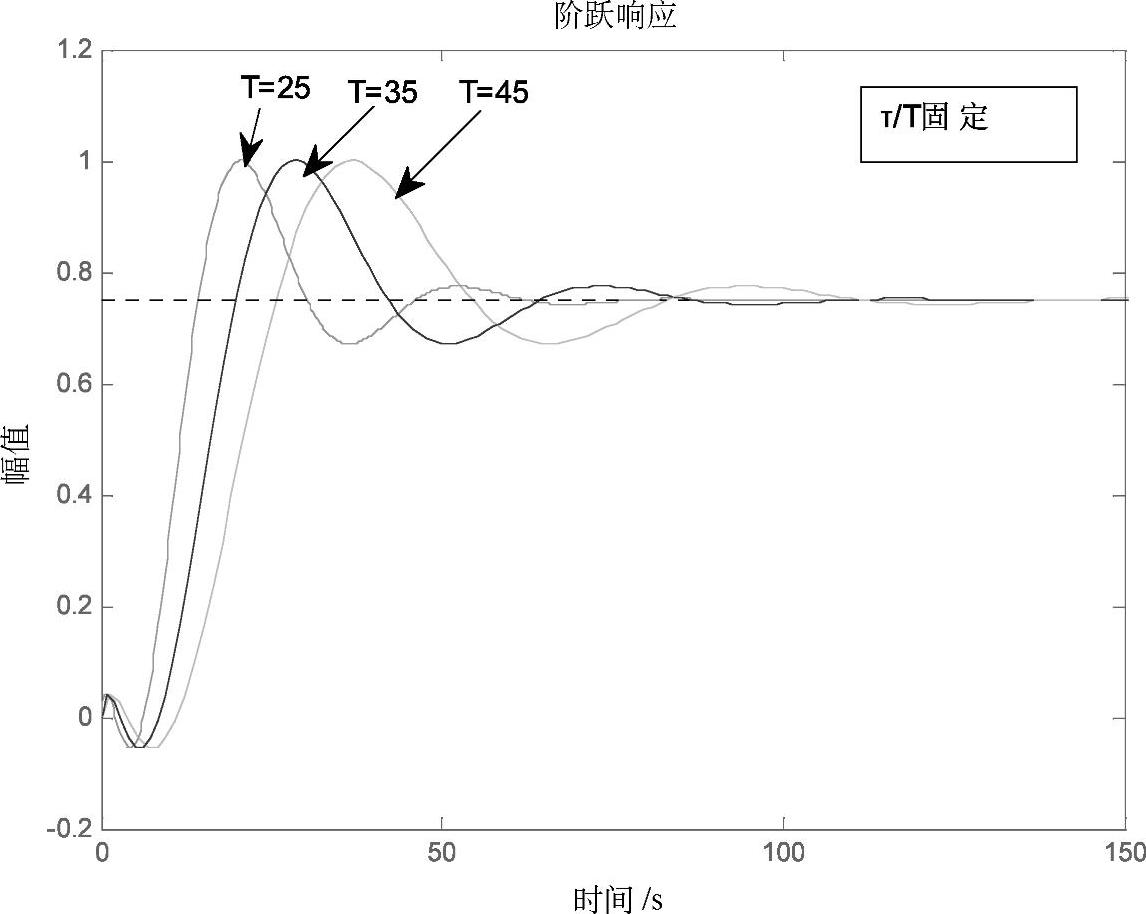
图4-10 控制通道不同时间常数下系统的单位阶跃响应曲线

设τ₀＝10，控制通道时间常数T分别为25、35、45时系统的单位阶跃响应曲线如图4-10所示。

(5)扰动通道时间常数的影响

扰动信号作用下，在不考虑系统的时滞时，控制系统输出的拉普拉斯变换式为

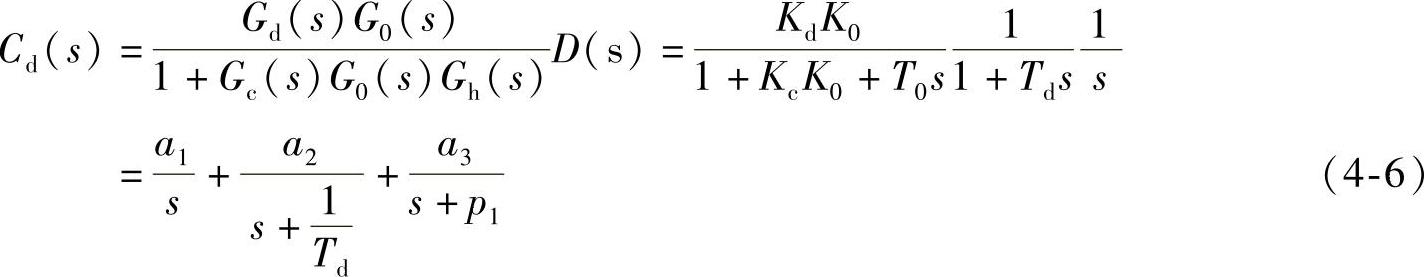
式中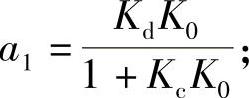

式（4-6）的拉普拉斯反变换为

c_d（t）＝a₁+a₂e^-1/Tdt+a₃e^-p1t （4-7）

由式（4-6）和式（4-7）可以看出，系统扰动通道的时间常数T_d越大，该极点离虚轴越近，对应暂态响应的指数上升越缓慢，即扰动对系统输出的影响越缓慢，有利于系统克服干扰的影响，控制系统质量提高。反之，扰动通道的时间常数T_d越小，扰动对系统的输出作用越大，系统对干扰的克服不及时。

当T₀/T_d＞1时，控制通道对系统的动态作用减缓，而扰动通道对系统的动态作用加快，控制系统的动态品质变差；

当T₀/T_d＜1时，控制通道对系统的动态作用加快，而扰动通道对系统的动态作用减缓，控制系统的动态品质变好。

设T₀＝35，改变扰动通道的时间常数T_d分别为10、35、50下系统的扰动阶跃响应曲线如图4-11所示。

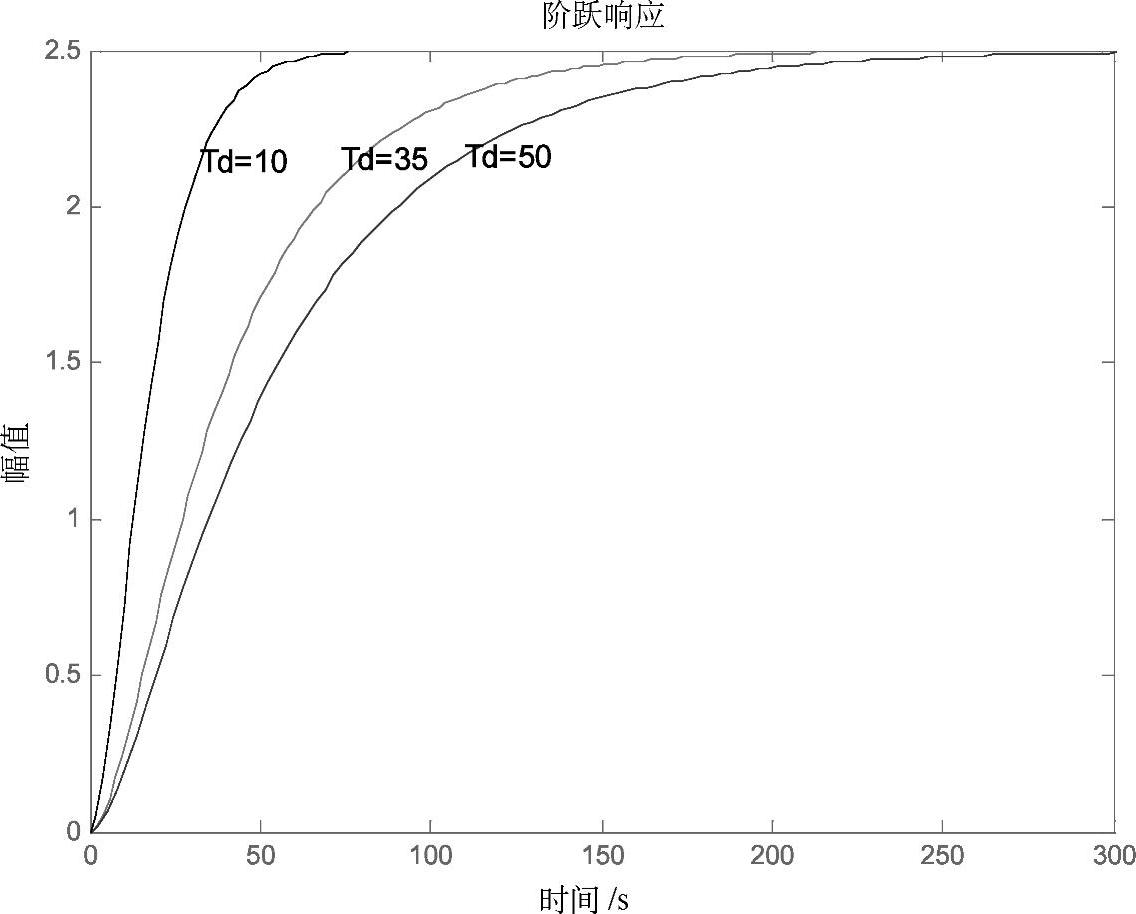
图4-11 扰动通道不同时间常数下系统的扰动阶跃响应曲线

（6）控制通道时滞的影响

时滞τ₀指输出变量的变化落后于输入变量变化的时间。滞后的产生是由于介质的输送或热质传递需要一段时间所引起的，滞后时间τ₀也反映了被控对象的动态特性。

控制通道时滞τ₀为15、30、45时，系统Simulink仿真及响应曲线如图4-12所示，控制系统通道时滞τ₀越大，系统的动态偏差越大，系统超调量增大，过渡过程时间拖长，甚至导致系统不稳定。因此，为提高控制质量应使控制通道中的时滞尽可能小。

用τ₀/T₀反映系统时滞的相对影响。当τ₀/T₀＞0.2时，简单控制系统已很难满足要求，要考虑采用复杂控制方案。在设计和确定控制方案时，设法减小τ₀值是必要的。例如，减小信号的传输距离和提高信号传输速度等。

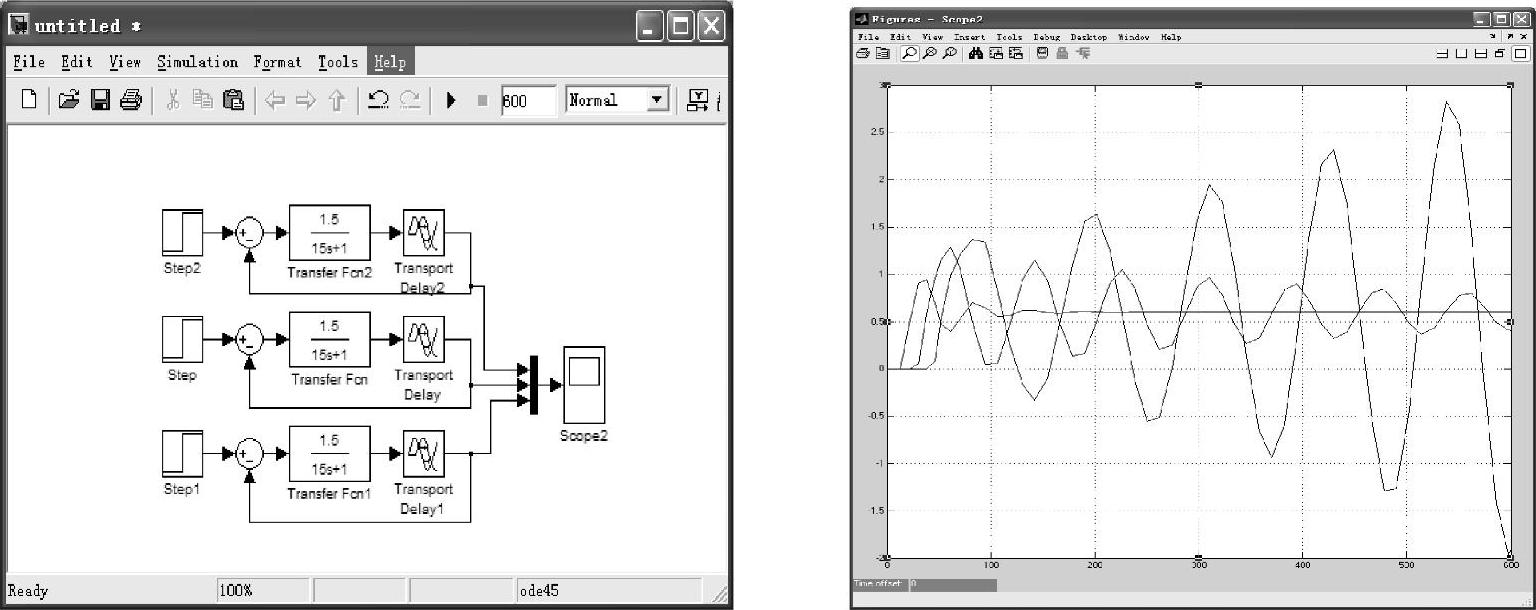
图4-12 控制通道不同时滞的系统阶跃响应

（7）扰动通道时滞的影响

从系统的特征方程可以看到，扰动通道的时滞τ_d不会影响系统的特征值。因此，扰动通道的时滞对系统的稳定性没有影响，它仅仅表示扰动进入系统的时间先后，对系统的动态品质没有影响。

（8）扰动作用点的影响

扰动作用点离被控变量越远，扰动通道的时间常数越大，扰动对系统的影响越缓慢。

当工艺上允许有几种控制参数可供选择时，可根据被控过程扰动通道和控制通道特性，对控制质量的影响作出合理的选择。所以正确选择控制参数就是正确选择控制通道的问题。

另外，当被控对象传递函数有多个时间常数时，各时间常数的匹配对控制系统质量也有影响。