如何进行PID调节器参数的工程整定

PID调节器参数的工程整定指确定PID调节器的比例度δ、积分时间常数T_I、微分时间常数T_D和采样周期T_s的具体数值。参数整定的实质是通过调节调节器的参数，使控制系统的动、静态特性得以改善，获得最佳的控制效果。

3.9.3.1 现场凑试法

它是根据经验先将调节器的参数设置在某些数值上，然后直接在闭合的控制系统中通过改变给定值和施加扰动信号，观测系统的输出响应曲线和扰动响应曲线的形状，根据δ、T_I和T_D对控制系统的影响规律、现场凑试调整相应的参数，直到获得满意的动、静态特性为止。

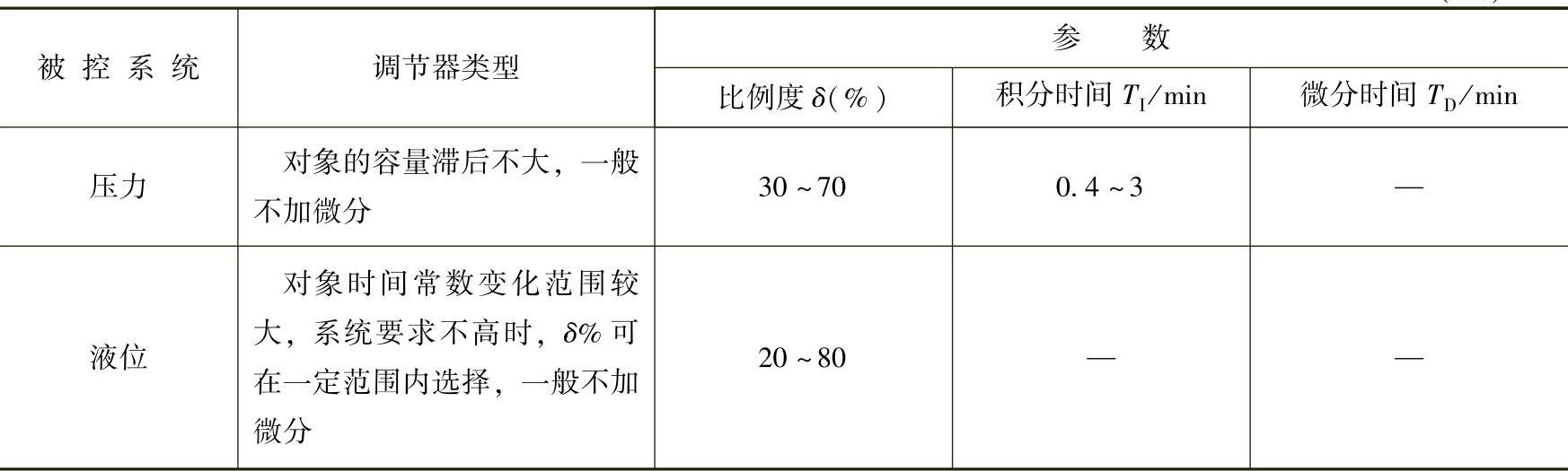
根据经验，不同被控对象下调节器参数的参考范围见表3-2。

表3-2 不同控制系统调节器参数的经验值

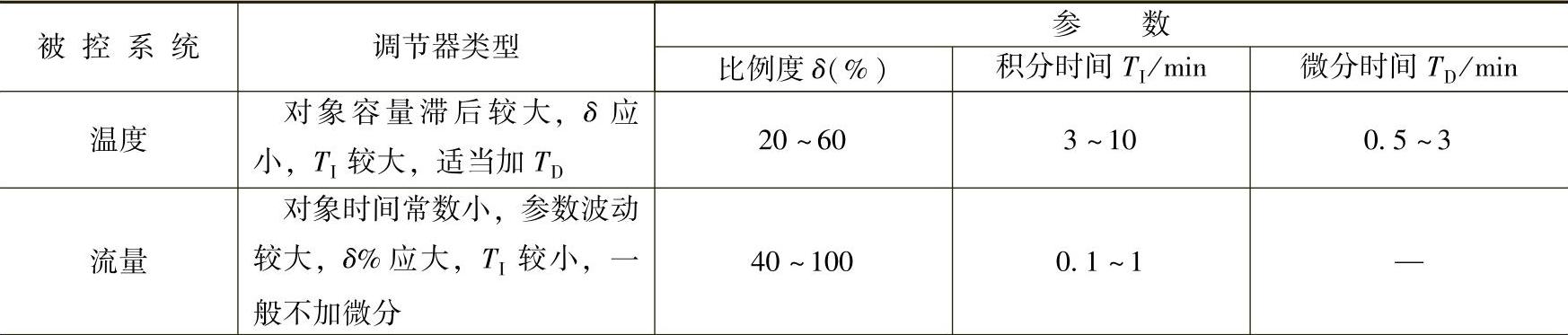
（续）

通常凑试的过程是按照先比例（P）、再积分（I）、最后微分（D）的顺序。具体步骤为：

1）先置调节器积分时间T_I＝∞，微分时间T_D＝0，在比例度δ按经验值设置的初值条件下，将系统投入运行，整定比例度δ。求得满意的4∶1（定值控制系统）或10∶1（随动控制系统）的过渡过程响应曲线。

2）引入积分作用（此时应将上述比例度δ加大10％～20％），将T_I由大到小进行整定。

3）若需引入微分作用时，则将T_D按经验值或按T_D＝（1/3～1/4）T_I设置，并由小到大加入。

这种方法简单、方便、可靠，对响应曲线较不规则的控制系统、外界干扰频繁的系统比较适合，但这种方法主要靠经验，参数凑试较费时间。

3.9.3.2 动态特性参数法

以广义被控对象阶跃响应为依据，根据经验公式求取PID调节器的最佳参数整定值。这是一种开环的整定方法，由齐格勒-尼科尔斯（Ziegler-Nichols）提出。

在系统开环并处于稳定的情况下，给系统输入一个阶跃信号，测量系统的输出响应曲线，一般的响应曲线如图3-37所示，该曲线也可采用曲线拟合法得到。

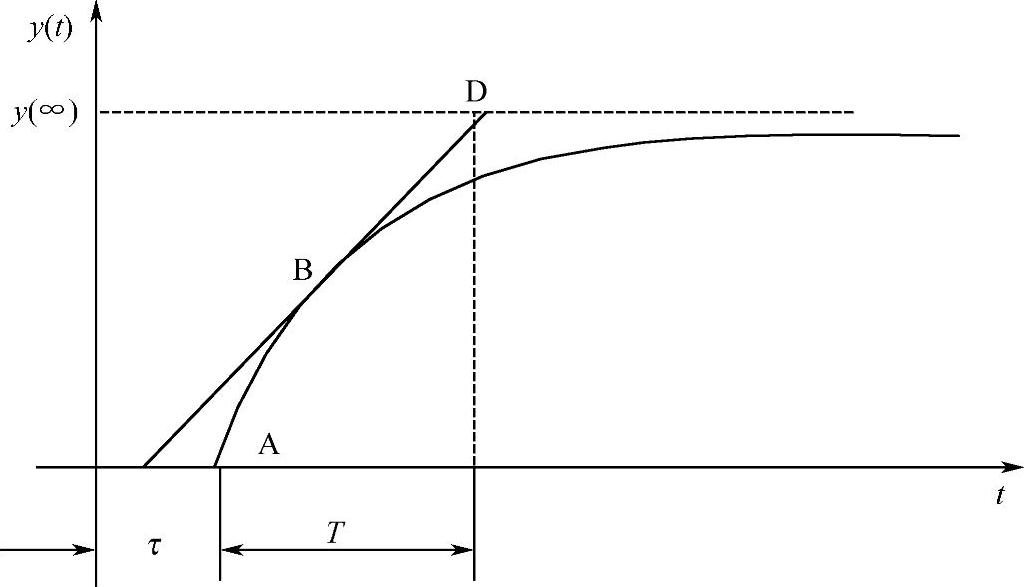
图3-37 被控对象的阶跃响应曲线

将广义对象用一阶惯性加纯滞后来近似，即广义对象的数学模型为

被控对象的增益K＝[Δy/（y_max-y_min）]/[Δu/（u_max-u_min）]，时间常数T和时滞τ如图3-37所示。

齐格勒-尼科尔斯（Ziegler-Nichols）法控制器参数整定见表3-3。

表3-3 Ziegler-Nichols控制器参数整定

后来不断改进，总结出一些计算控制器最佳参数整定公式，如柯恩-库恩（Cohen-Coon）整定见表3-4。

表3-4 Cohen-Coon控制器参数整定

例如假定广义被控对象的传递函数如下：

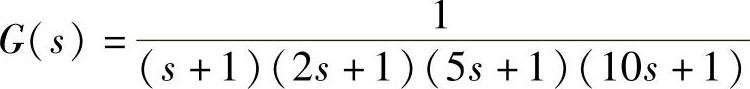
试采用动态特性参数法整定P、PI、PID控制器的参数。

M函数程序：

采用曲线拟合法，得拟合曲线如图3-38所示，由此可近似得到广义被控对象的一阶惯性加纯滞后对象数学模型的参数为K＝1.0322，T＝14.1229s，τ＝5.4992s。

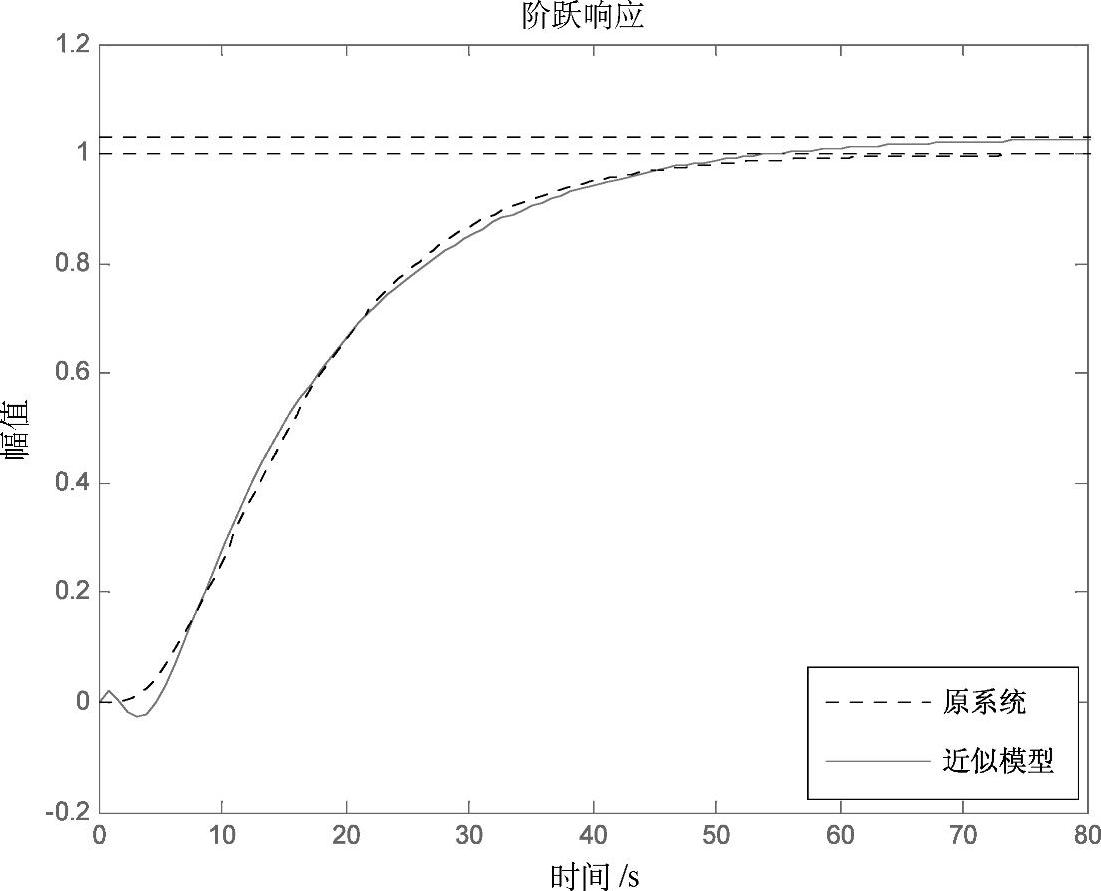
图3-38 广义对象及近似一阶惯性加纯滞后对象的开环响应曲线

采用Ziegler-Nichols控制器参数整定得：PI调节器的δ％＝44.2％，积分时间T_I＝18.15s，系统的单位阶跃响应曲线如图3-39所示，系统的最大超调量为30％，峰值时间为17s，过渡过程时间为58s。

采用Cohen-Coon控制器参数整定法得：PI调节器的参数K_P＝2.32，δ％＝43.1％，积分时间常数T_I＝10.2s，系统的单位阶跃响应曲线如图3-40所示，系统的最大超调量为61％，峰值时间为17.3s，过渡过程时间为82s。

3.9.3.3 临界比例度法

临界比例度法是一种闭环的参数整定方法。它是基于纯比例控制系统临界振荡的试验数据——临界比例带δ_k和临界振荡周期T_k。采用一些经验公式，获取控制器的最佳参数整定值，具体整定步骤如下：

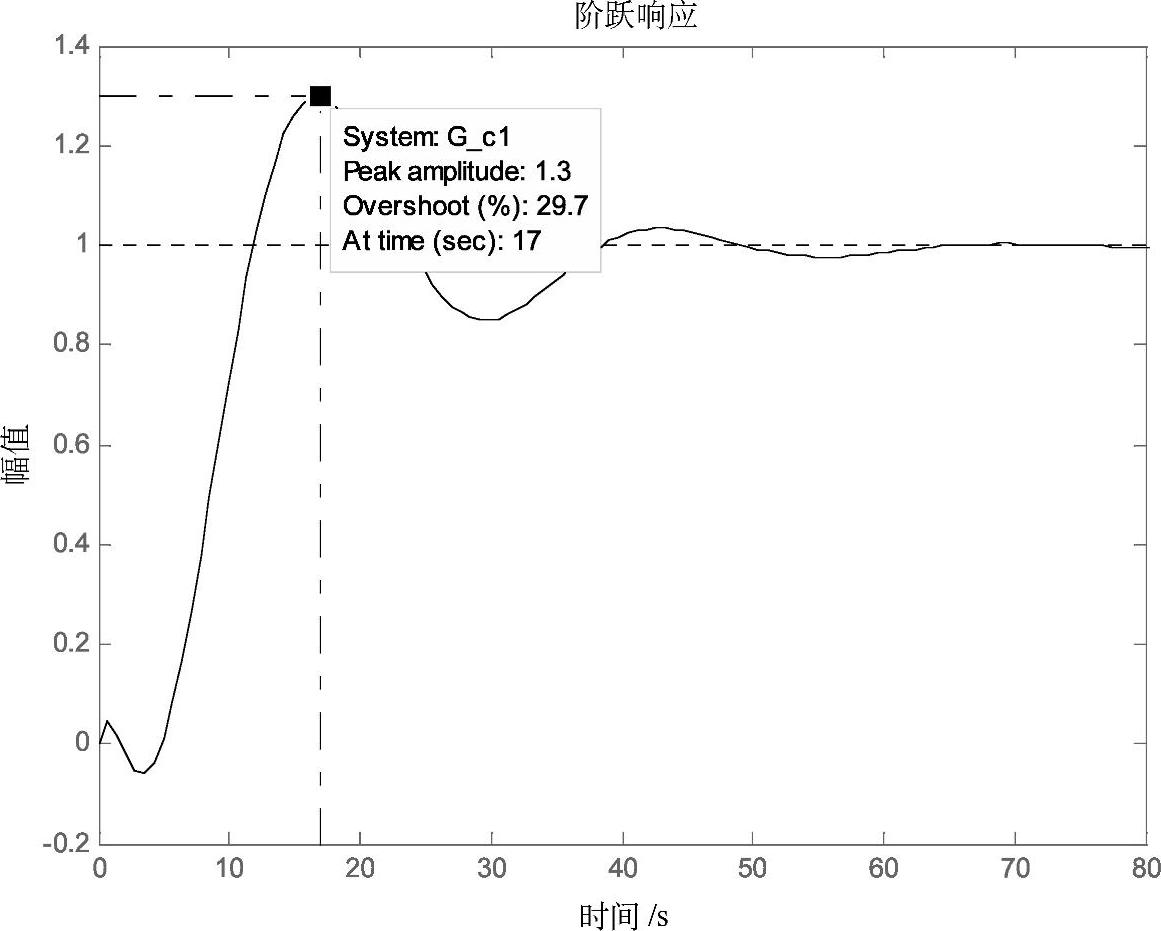
图3-39 Ziegler-Nichols参数整定下系统的单位阶跃响应曲线

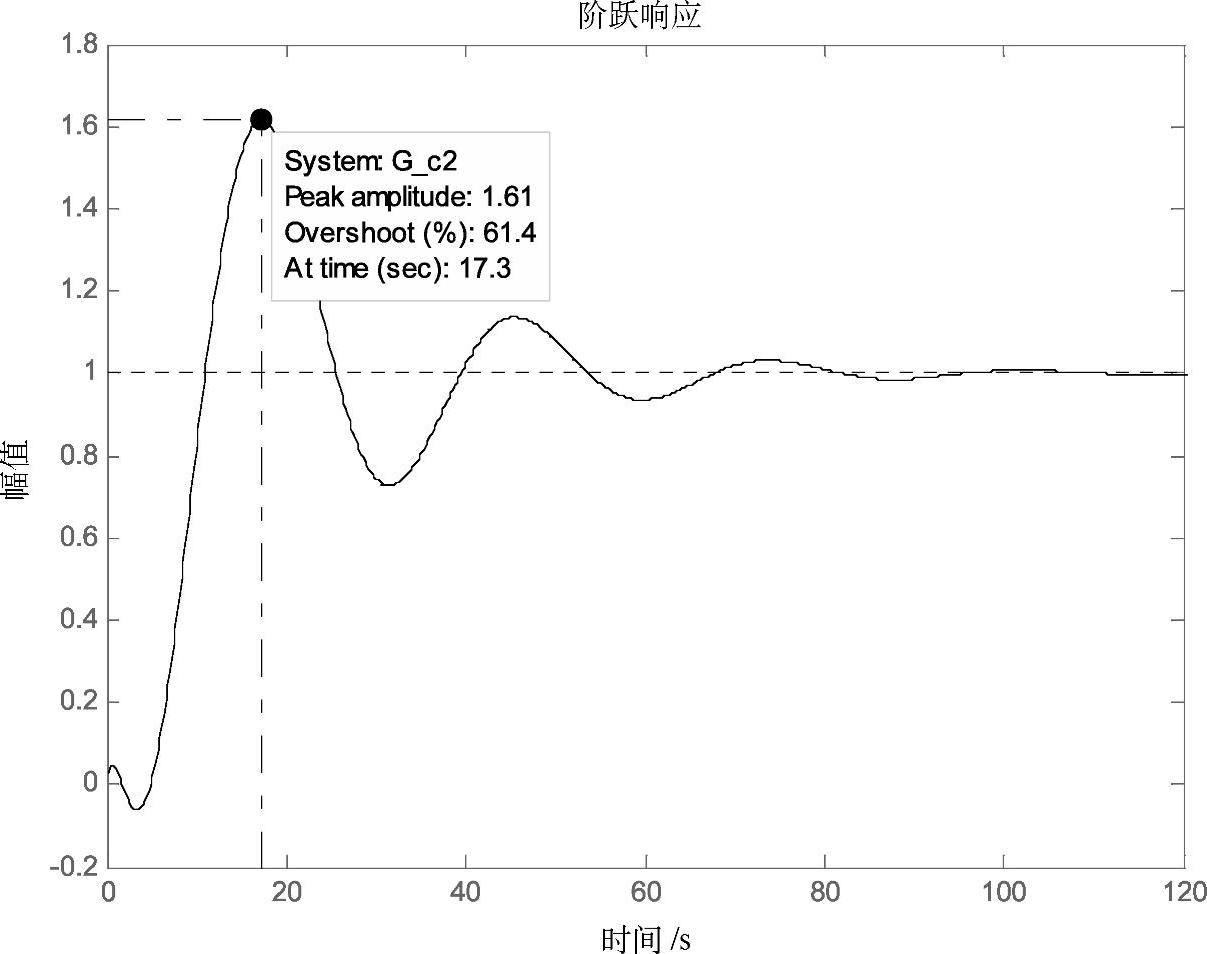
图3-40 Cohen-Coon参数整定下系统的单位阶跃响应曲线

1）在构成闭环的控制系统中，将控制器置于纯比例作用，从大到小逐渐改变控制器的比例度δ，直到系统出现如图3-41所示的等幅振荡的过渡过程。此时的比例度称为临界比例度记为δ_k，相邻两个波峰间的时间间隔称为临界振荡周期记为T_k。

2）根据临界比例度δ_k和临界振荡周期T_k的值，按表3-5中的经验公式，计算控制器的最佳整定参数。

临界比例度法整定控制器参数时的注意事项为：

1）控制规律的确定按“先P后I最后D”的操作程序将控制器参数整定到最佳参数值上。

2）由于被控对象特性的不同，按上述经验公式求得的控制器参数不一定都能获得满意的动、静态特性，为此可将计算值作进一步调整。比如，控制系统的超调量或最大偏差较大时，可将计算的比例度增大1.5倍左右。

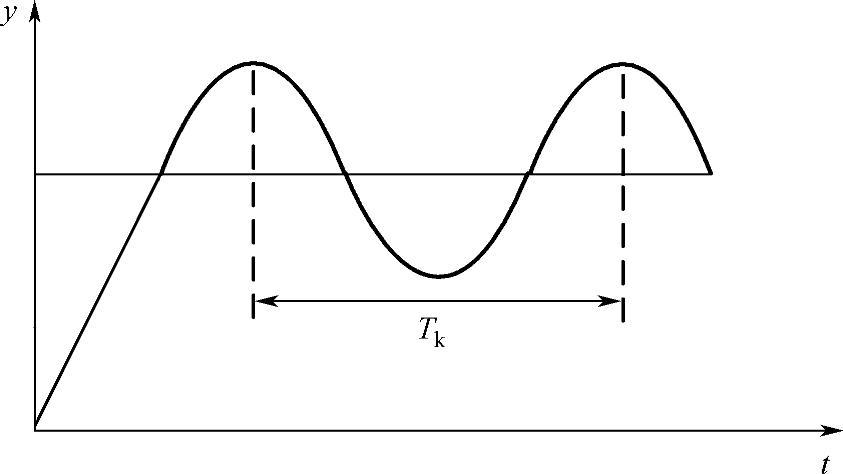
图3-41 闭环系统的临界振荡过程曲线

表3-5 临界比例度法参数整定公式(www.xing528.com)

3）对于有些过程控制系统（锅炉水位控制或时间常数较大的单容对象），临界比例度很小，使系统接近位式控制，调节阀不是全关就是全开，对工业生产不利。

4）对于有的过程控制系统，当调节器比例度δ调到最小刻度值时，系统仍不产生等幅振荡。对此，就把最小刻度的比例度作为临界比例度δ_k进行控制器参数整定。

3.9.3.4 衰减曲线法

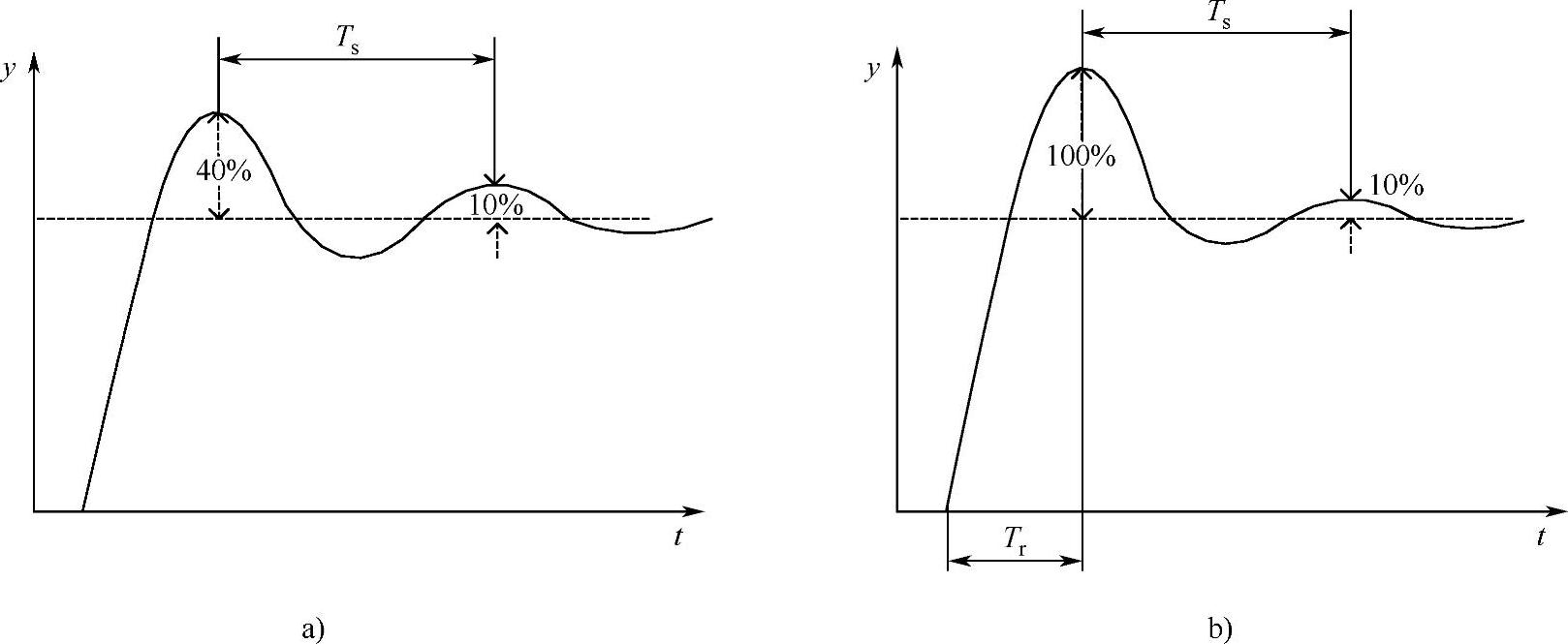
图3-42 系统衰减曲线

a）衰减比4∶1 b）衰减比10∶1

衰减曲线法也是一种闭环的参数整定方法，它是基于控制系统过渡过程响应曲线的衰减比为4∶1（定值控制系统）或10∶1（随动系统）的试验数据，利用一些经验公式，确定控制器的最佳参数值。具体整定的步骤为：

1）首先将过程控制系统中控制器参数置成纯比例作用（T_I＝∞，T_D＝0），使系统投入运行。

2）待系统稳定后，作设定值的阶跃扰动，并观测系统的响应曲线。同时调整比例度δ的变化，直到系统响应曲线出现4∶1（或10∶1）的衰减过程曲线，如图3-42所示。此时的比例度为4∶1（或10∶1）衰减比例度δ_s，两个相邻波峰间的时间间隔称为4∶1（或10∶1）的衰减振荡周期T_s。

3）利用δ_s和T_s的值，按表3-6给出的经验整定公式，求取控制器的最佳参数整定值。

表3-6 衰减曲线法整定公式

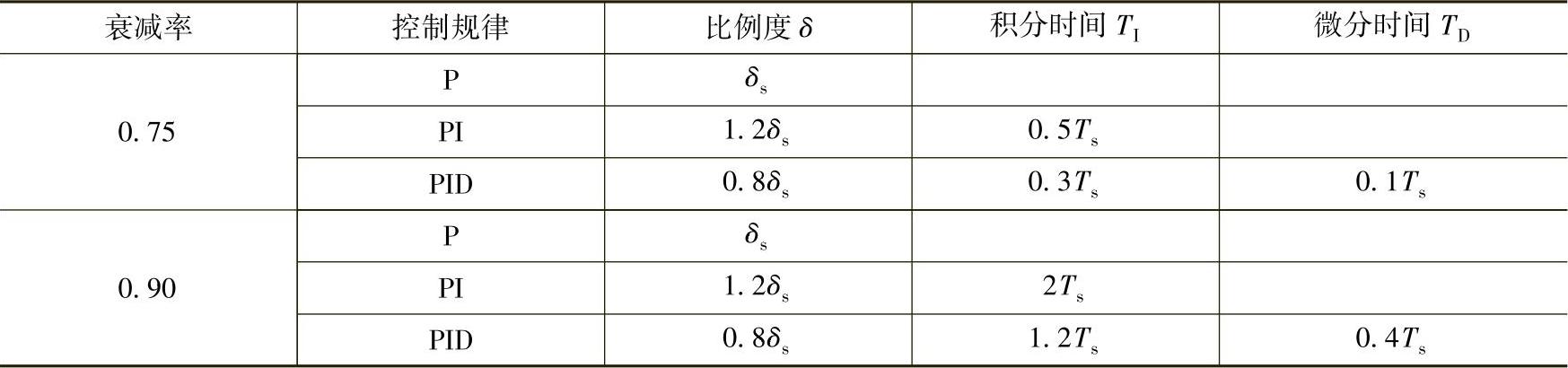
衰减曲线法整定控制器参数时的注意事项有：

1）对于反应较快的控制系统，要准确确定4∶1衰减曲线和读出T_s比较困难，此时可用记录指针来回摆动两次就达到稳定，作为4∶1衰减过程。

2）在生产过程中，负荷变化会影响过渡过程特性。当负荷变化较大时，必须重新整定调节器参数值。

3）对于随动系统宜应用10∶1衰减响应过程。对于10∶1衰减曲线法整定控制器参数的步骤与上述完全相同，此时衰减振荡周期T_s更难确定，为此可以系统响应曲线的上升时间T_r作为衰减振荡周期T_s，仅计算公式略有不同。

假设被控对象的广义传递函数为

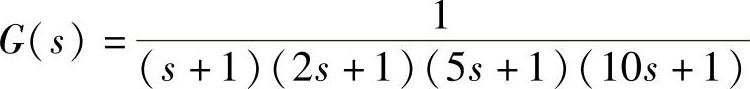
原系统的开环响应曲线和拟合曲线可将系统近似为自平衡非振荡过程，如图3-43所示，并得到K＝1.03，T＝14.12，τ＝5.5。

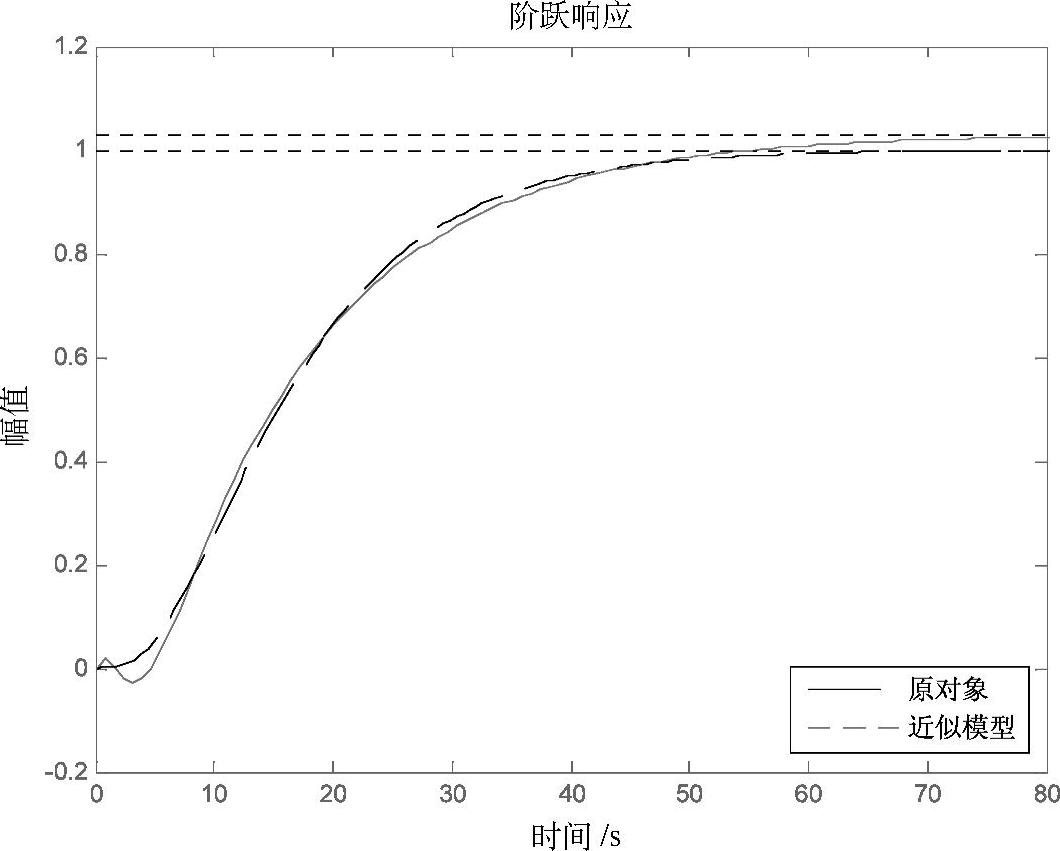
图3-43 原系统的开环响应曲线和系统的拟合曲线

采用Ziegler-Nichols法整定PI调节器参数，得δ＝44.2％，T_I＝18.15，此时控制系统的单位阶跃响应曲线如图3-44所示，系统的最大超调量为30％，峰值时间为17.3s，过渡过程时间为58s。

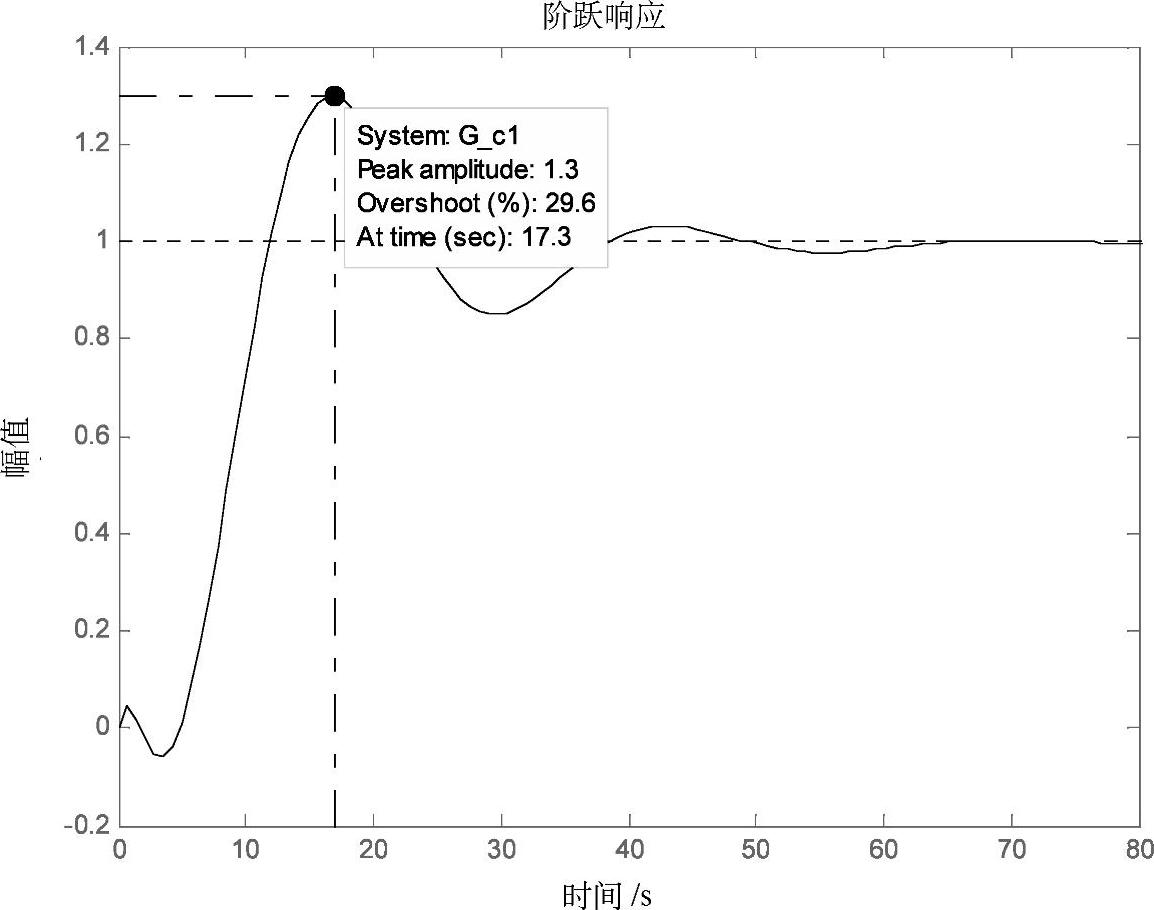
图3-44 Ziegler-Nichols法整定PI调节器的响应曲线

采用Cohen-Coon法来整定PI调节器参数，得δ＝44.2％，K_P＝2.32，T_I＝18.15，系统的单位阶跃响应曲线如图3-45所示，系统的最大超调量为61％，峰值时间为17.2s，过渡过程时间为83s。

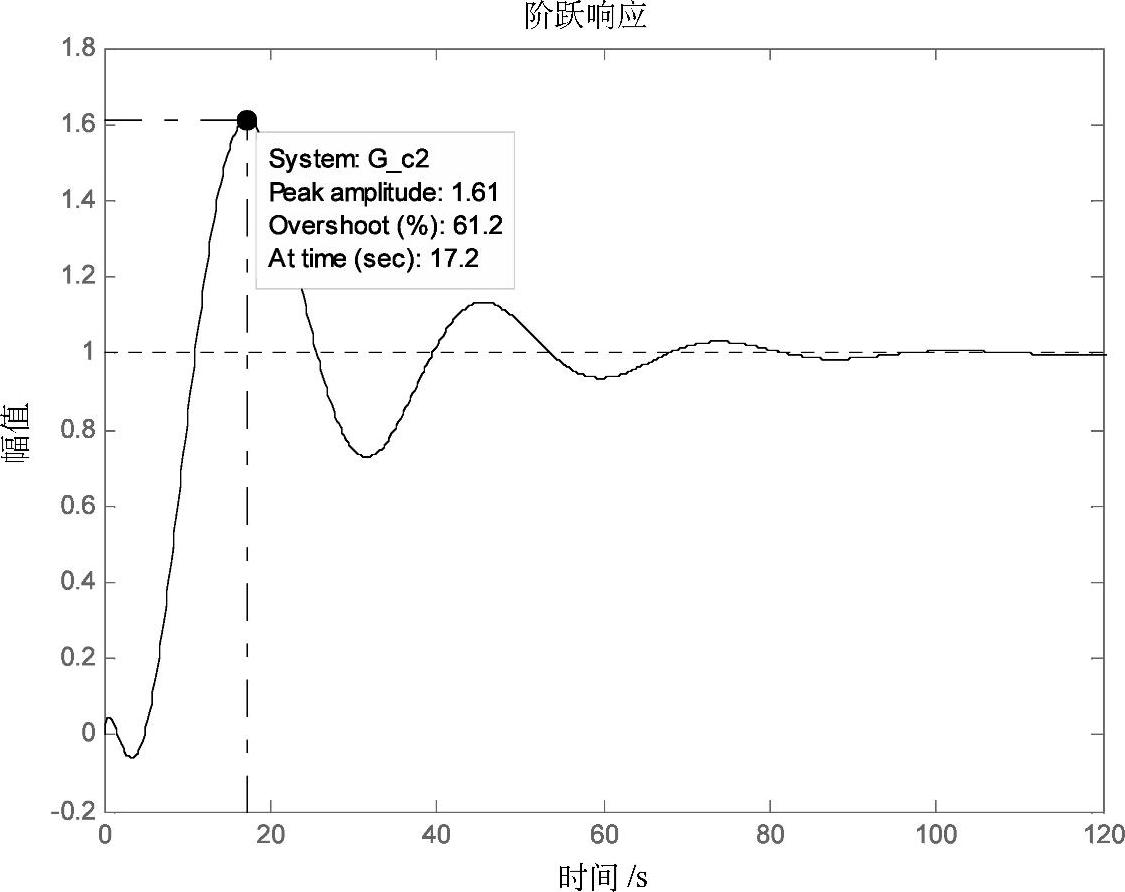
图3-45 Cohen-Coon法整定PI调节器参数的响应曲线

采用临界比例度法整定PID参数：将系统构成纯比例控制，由大到小改变比例度，观测系统的闭环响应曲线，图3-46所示分别为比例度δ＝25％、δ＝10％和δ＝13％的单位阶跃响应曲线。即当δ＝13％、K＝7.75时，系统输出响应出现等幅振荡，临界比例度δ_s＝13％，临界振荡周期T_s＝20s。

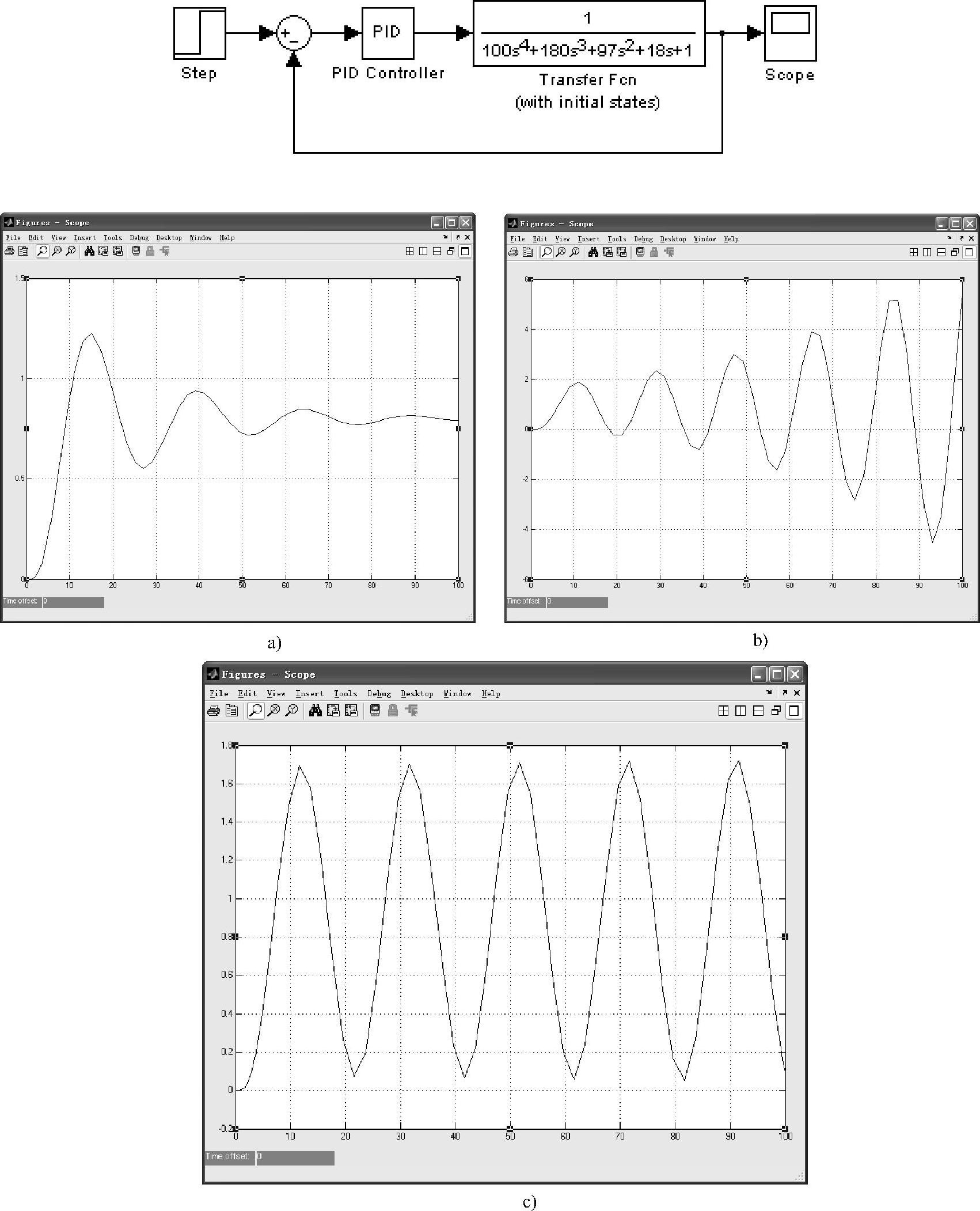
图3-46 不同比例度下系统的单位阶跃响应曲线

根据临界比例度δ_s＝13％，临界振荡周期T_s＝20s，由经验公式可确定不同控制规律下的调节器参数。采用比例（P）调节器：δ＝26％，系统的响应曲线如图3-47a所示；采用比例积分（PI）调节器：δ＝28.6％、T_I＝17s，系统的响应曲线如图3-47b所示；采用比例积分微分（PID）调节器：δ＝22.1％、T_I＝17s、T_D＝2.5s，系统的响应曲线如图3-47c所示。

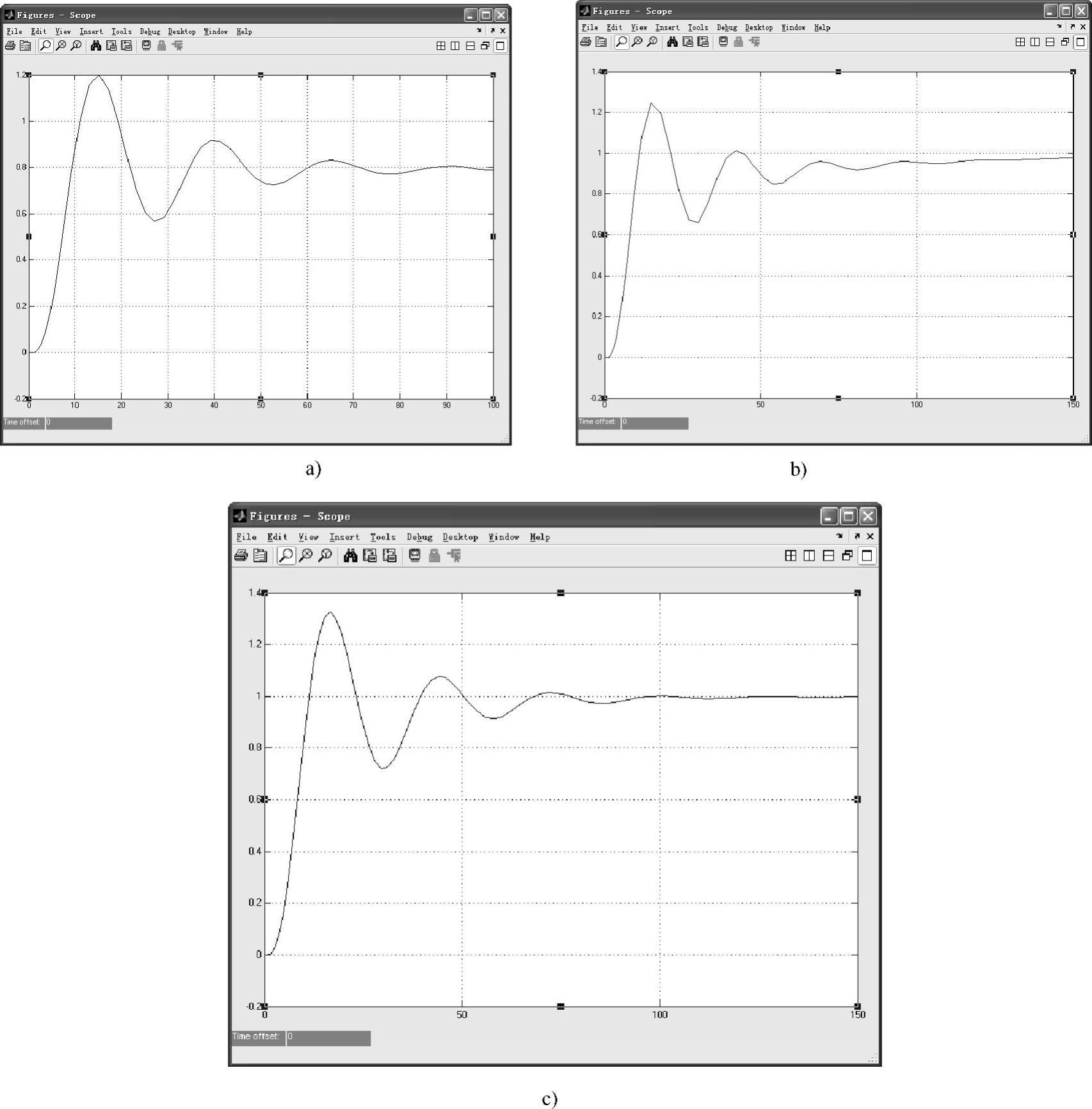
图3-47 不同控制规律下系统的响应曲线

a）P控制 b）PI控制 c）PID控制

为了说明三种不同控制规律对系统的影响，将P、PI、PID控制下的系统响应曲线作在同一坐标系中，如图3-48所示。

采用衰减曲线法整定调节器参数：将系统构成纯比例的闭环控制系统，改变调节器的比例度，观测系统的闭环响应曲线，如图3-49所示，分别为比例度δ＝22.2％、δ＝16.7％的单位阶跃响应曲线。进一步对比例度δ调整，当δ＝28.9％、K＝3.45时，响应曲线如图3-50所示，系统输出响应的衰减比为4∶1，对应的周期T_s＝42.4s-15.5s＝26.9s。

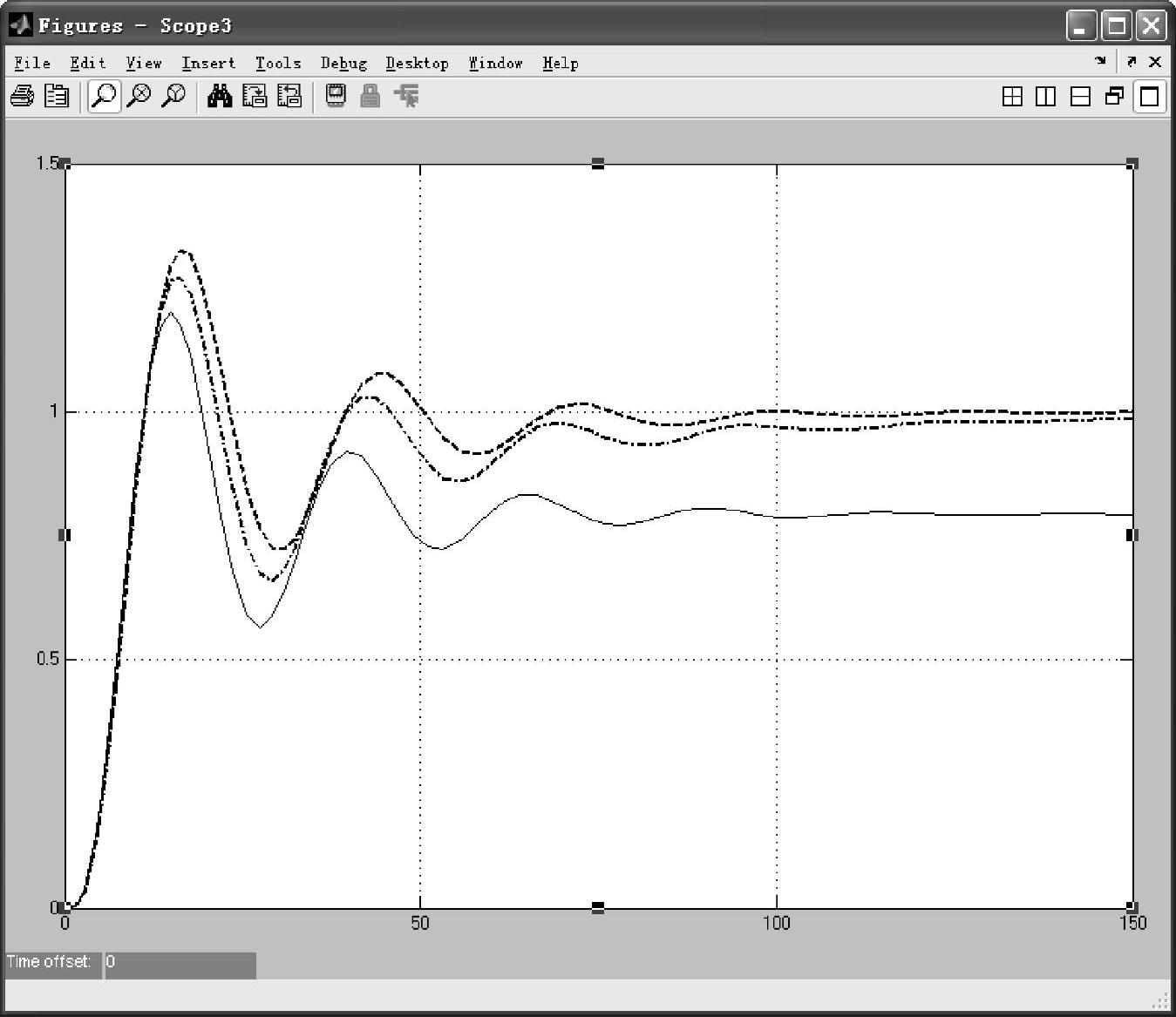
图3-48 P、PI、PID调节器作用下的系统响应曲线

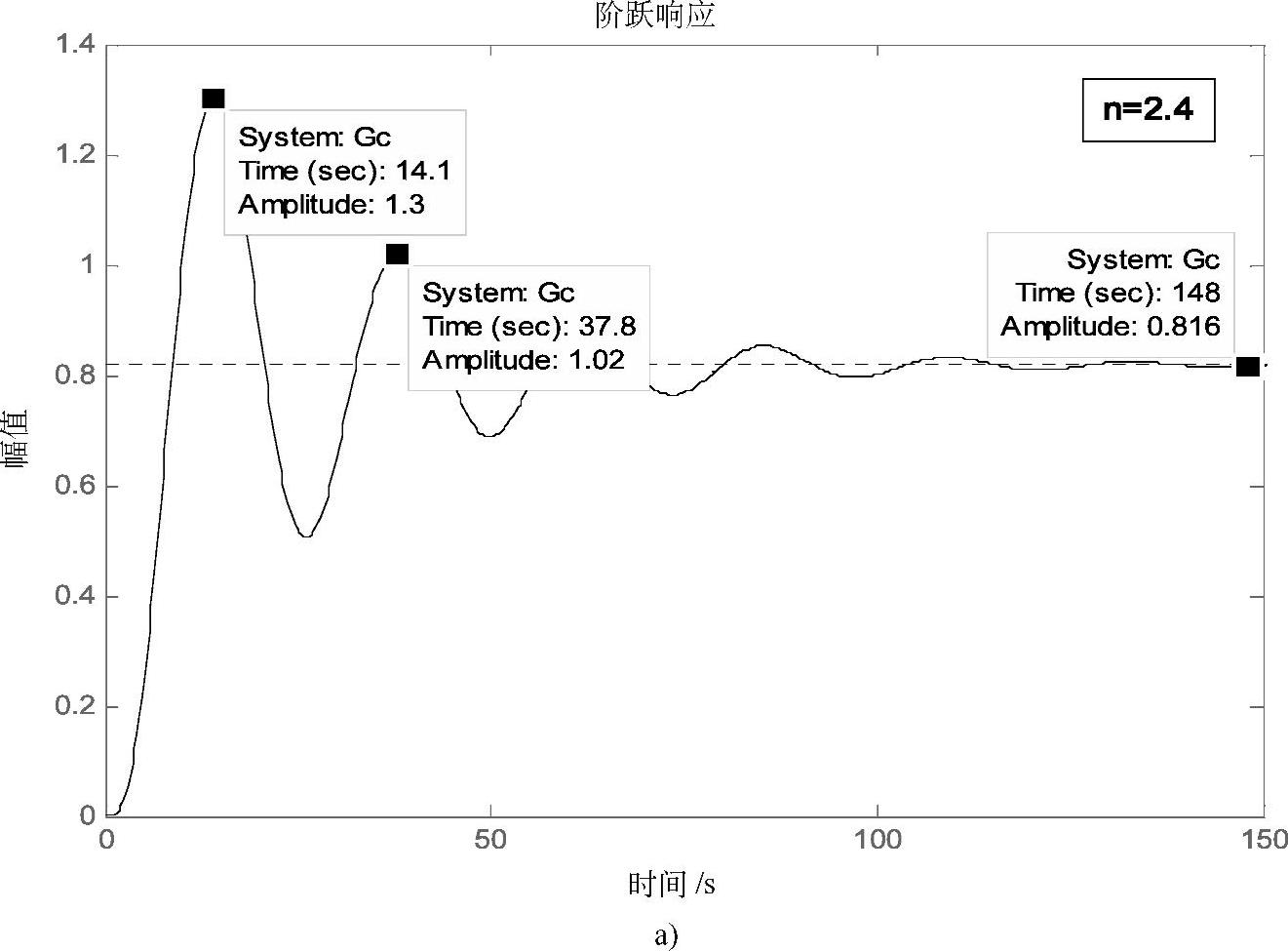
图3-49 不同比例度下系统的响应曲线

a）δ＝22.2％时系统的单位阶跃响应曲线

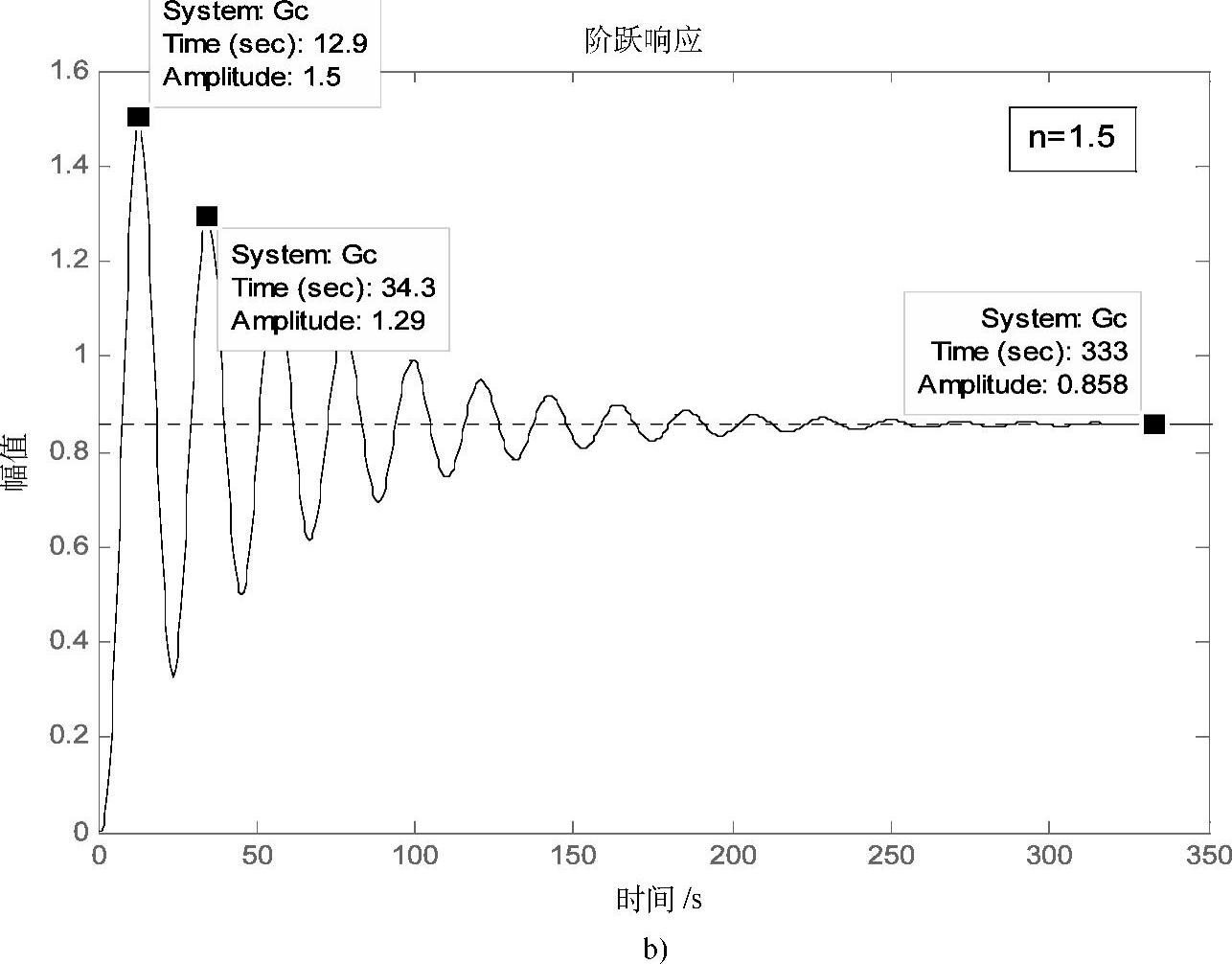
图3-49 不同比例度下系统的响应曲线（续）

b）δ＝16.7％时系统的单位阶跃响应曲线

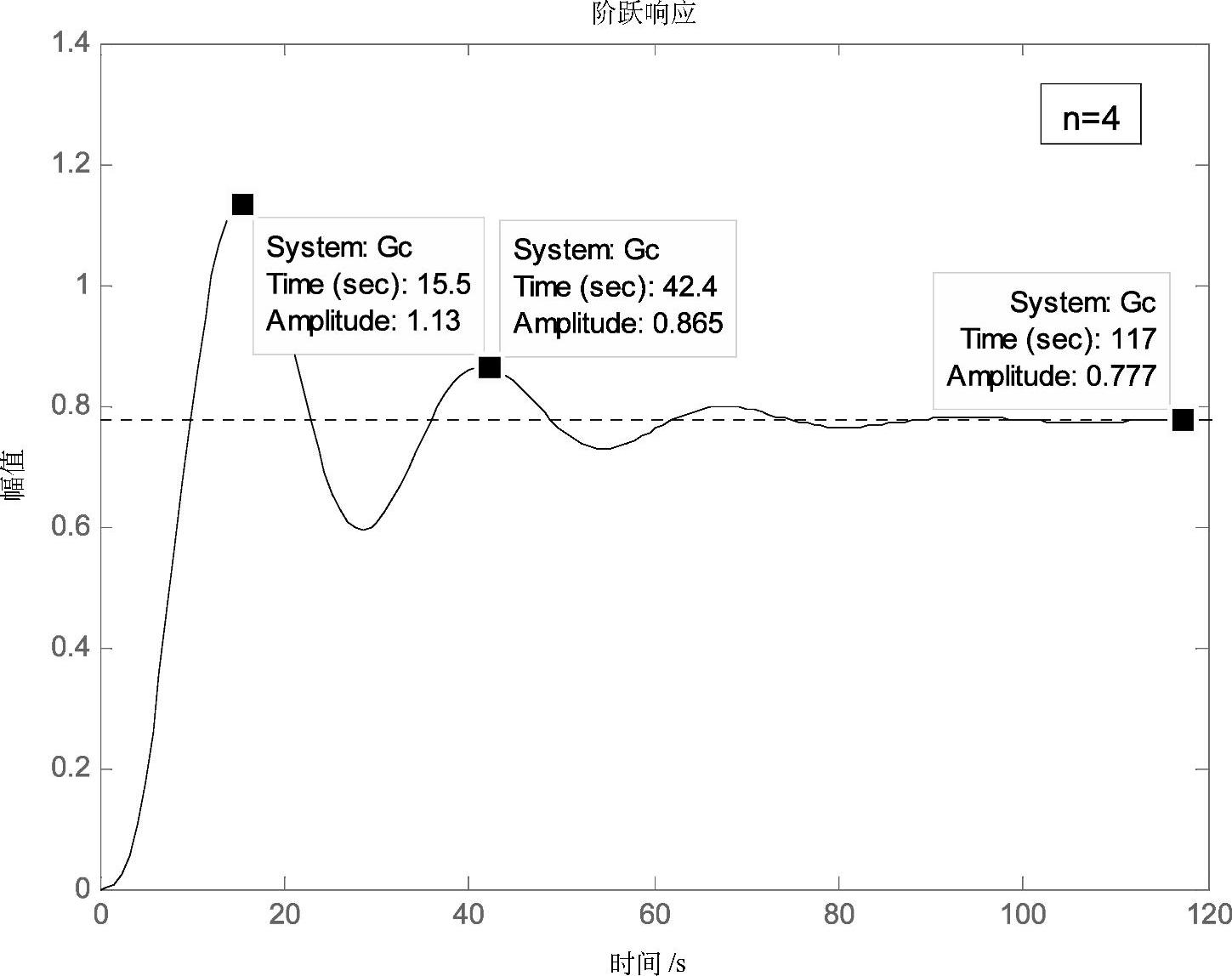
图3-50 δ＝28.9％时系统的单位阶跃响应曲线

采用衰减曲线法的经验公式，确定不同控制规律下调节器的参数。采用P调节器：δ＝29％（K_P＝3.45）；采用PI调节器：δ＝34.8％（K_P＝2.875），T_I＝13.45s；采用PID调节器：δ＝23.2％（K_P＝4.31），T_I＝8.1s，T_D＝2.7s，对应系统的单位阶跃响应曲线如图3-51所示。

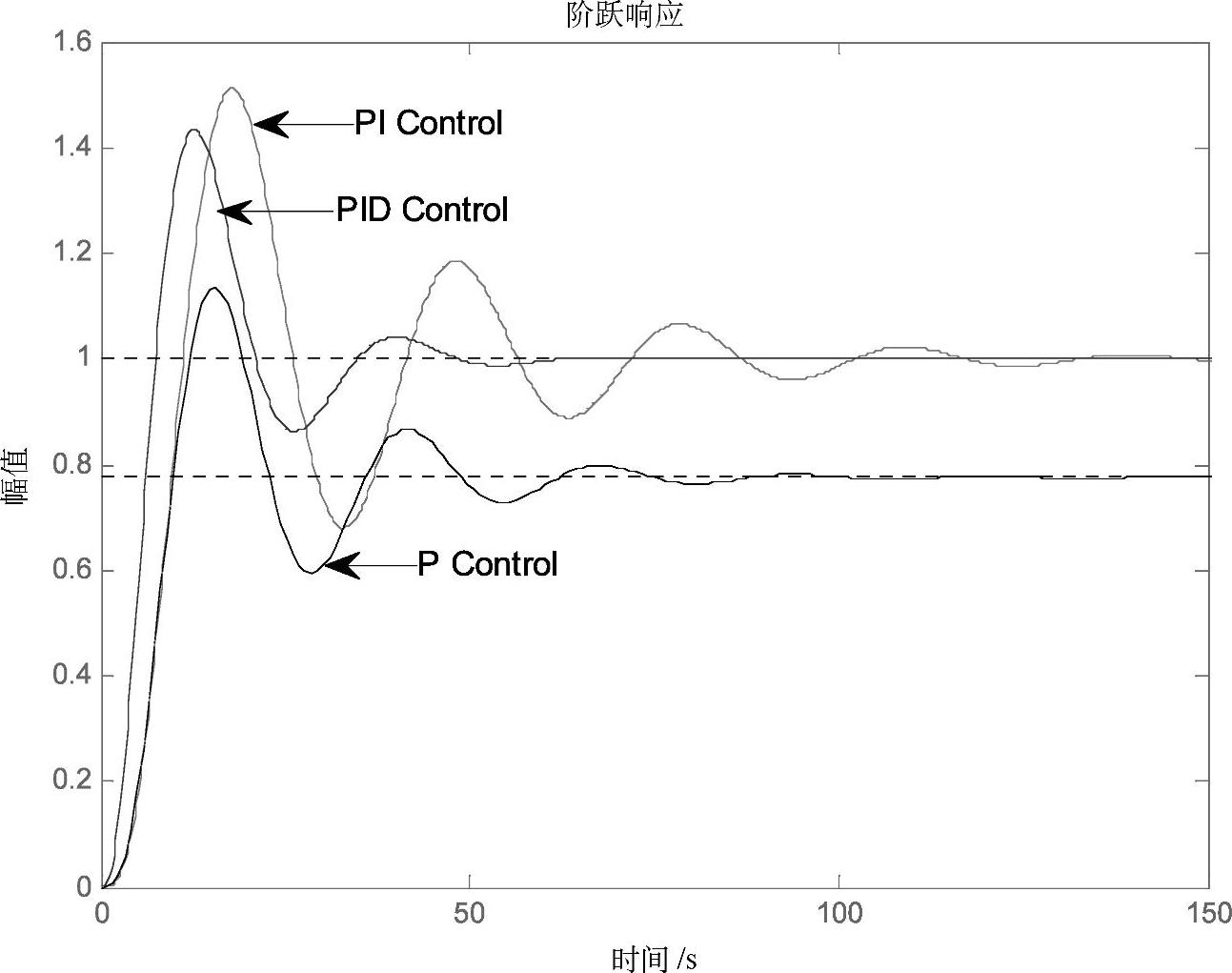
图3-51 不同控制规律下系统的响应曲线