【摘要】:对于太阳电池而言,需要做如下假设:1)若仅考虑带间产生,则Ge=Gh 2)在持续光照条件下,太阳电池一般工作在稳态,即电子浓度变化率和空穴浓度变化率均为。此时连续性方程进一步简化为对于太阳电池而言,其复合包含了辐射复合Urad、俄歇复合Uauger、陷阱复合Utrap和表面复合Usurf等物理过程。太阳电池非平衡载流子浓度的求解即采用上式。
为了更好地了解半导体内载流子的输运情况,这里以一维半导体输运方程组描述载流子的产生、复合、漂移和扩散问题。
一维空间中,连续性方程为[17]
对于晶体半导体材料,由第3章非平衡载流子统计分布与电流的讨论中可知
对于一维模型而言
所以,得到
此即半导体材料通用连续性方程。
对于太阳电池而言,需要做如下假设:
1)若仅考虑带间产生,则
Ge=Gh (4.136)(https://www.xing528.com)
2)在持续光照条件下,太阳电池一般工作在稳态,即电子浓度变化率和空穴浓度变化率均为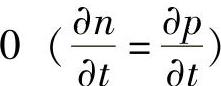 。
。
3)若所用太阳电池材料是理想的、高纯度的、不存在界面态,则内建电压Vbi只存在pn结内部,pn结可以看做由三个区域组成,它们分别是p型电中性区、耗尽区和n型电中性区。因此,电中性区不存在电场(F=0)。此时连续性方程进一步简化为
对于太阳电池而言,其复合包含了辐射复合Urad、俄歇复合Uauger、陷阱复合Utrap和表面复合Usurf等物理过程。由于各种复合具有相同的表达式。所以,定义n型半导体的总复合率Ue和p型半导体的总复合率Uh分别为[18]
式中
进一步化简连续性方程为
又因为少子寿命和扩散长度的关系
该组方程即为分析半导体器件的基本方程。太阳电池非平衡载流子浓度的求解即采用上式。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




