宏观表现：非平衡载流子在4.2.2中的产生

用“光子进、电流出”来形容太阳电池发电机理再贴切不过，其微观机理是载流子的量子跃迁产生非平衡载流子，非平衡载流子的定向输运产生电流；宏观表现是具有一定吸收系数的半导体材料吸收入射光产生电流的过程。因此，了解半导体材料吸收系数和朗伯-比尔定律是太阳电池物理重要的内容之一。

1.吸收系数的定义

吸收系数α表示了入射光经过材料后的衰减程度，是单位体积内各种光吸收截面的叠加。

设一辐照度为P（E，0）的单色光照射到半导体材料表面，如图4.4所示。若不考虑材料的反射率，在材料内部x处，辐照度衰减为P（E，x），在经过dx的距离，辐照度进一步衰减为

dP（E，x）=-α（E，x）P（E，x）dx （4.21）

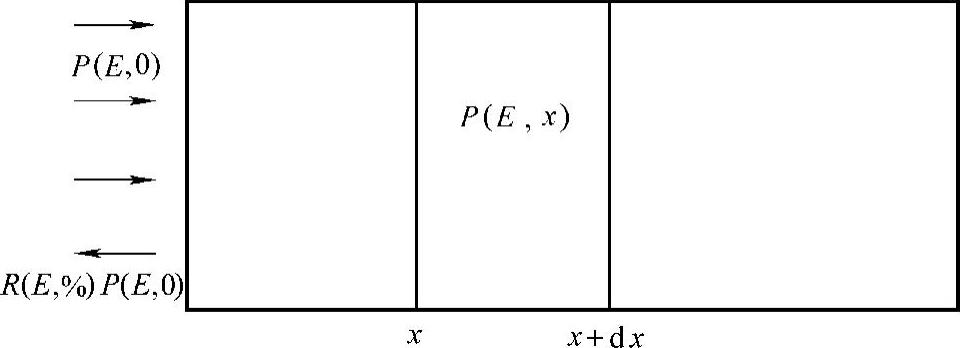
图4.4 材料对入射光的吸收和反射

对上式进行积分，得到辐照度随位置的变化关系为

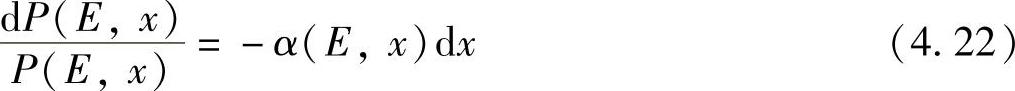
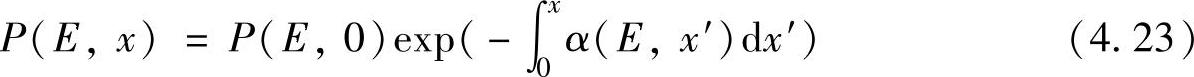
如果半导体材料对入射光的吸收是均匀的，即α不是位置x的函数，则上式简化为^[6]

P（E，x）=P（E，0）e^-αx （4.24）

若入射光是单色光，且α不是波长的函数，上式进一步简化为

P（x）=P（0）e^-αx （4.25）此即著名的朗伯-比尔定律，它表明了辐照度随吸收系数α发生指数衰减^[7]。

若考虑材料的反射率，辐照度随位置的变化关系可进一步精确表达为

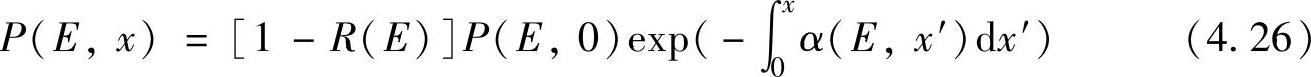
2.吸收系数的表达式

由朗伯—比尔定律可知，吸收系数α严格地反映了材料对光吸收性能的好坏，如果能得到α的通用表达式，以后的工作就会方便许多。下面将运用波印亭矢量来给出吸收系数α的表达式。

由电磁学可知，光是一种电磁波，光的传播可以用平面波表示，它反映了光波电场强度E（r，t）随空间位置和时间的变化，即

式中 E₀——平面波振幅矢量，表示平面波的偏振方向，E₀表示了电场强度E的大小；

k——平面波的波矢；

r——空间位置坐标；

ω——平面波的角频率（s^-1）。

如果平面波在x轴方向传播，则平面波表达式为

若电磁波在介质中传播，则

式中 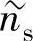——半导体的折射率。

半导体折射率通常具有复数形式^[8]，即

式中 κ_s——消光系数，半导体折射率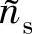的虚部。(www.xing528.com)

将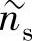表达式带入式（4.28）中，平面波表达式进一步写为

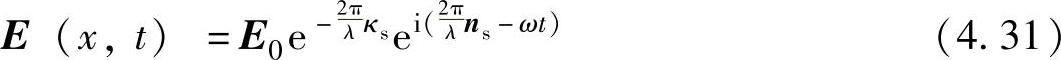
由波印亭矢量（电磁场中的能流密度矢量）的定义式与辐照度的关系^[58]，有

S=E×H （4.32）

式中 H——光波的磁场强度分量（A/cm）。

利用下面的关系式：

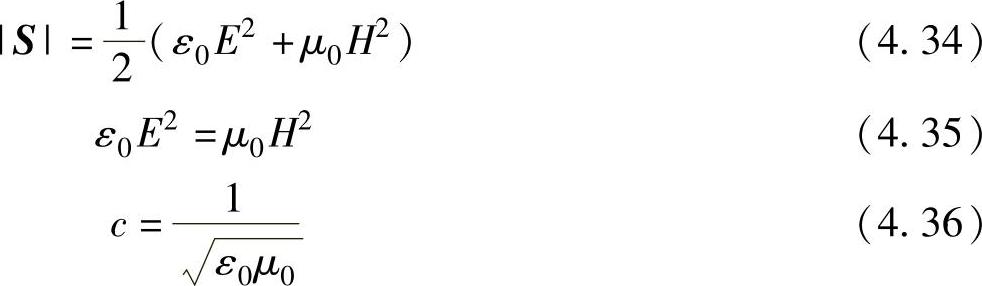
得到

对比朗伯—比尔定律与上式，得到

由上式可见，吸收系数α是入射光波长λ和消光系数κ_s的函数，也可以说吸收系数是入射光能量E、波长λ或频率v的函数。

3.非平衡载流子产生率与吸收系数的关系

对于半导体材料，常设定其吸收系数α的倒数为吸收长度，即理论上认为在吸收长度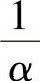范围内，入射光得以全部衰减。实际上，在一个吸收长度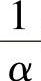范围内，入射光衰减为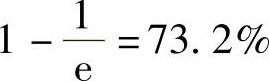。吸收系数是半导体材料一个非常重要的物理量，特别是对太阳电池厚度的设计来说至关重要。

假设能量为E、光子通量为b_s（E，T_s）的一束光照射到面积为S的太阳电池表面，则太阳电池吸收到入射光子数为b_s（E，T_s）S。那么，单位体积内吸收光子数为

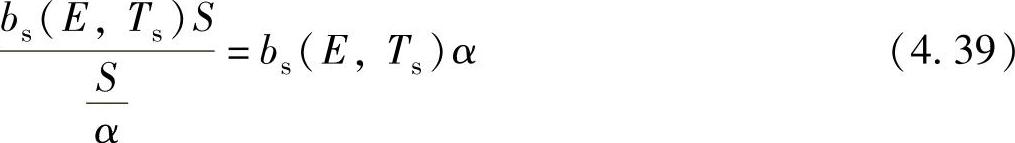
假设，材料每吸收一个光子均可以产生一对光生电子—空穴对，则载流子的光谱产生率为^[3]

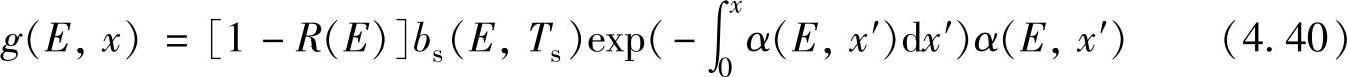
式中 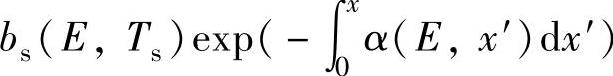——任意深度范围光子通量衰减的程度。进一步对入射光能量进行积分，得到产生率G为

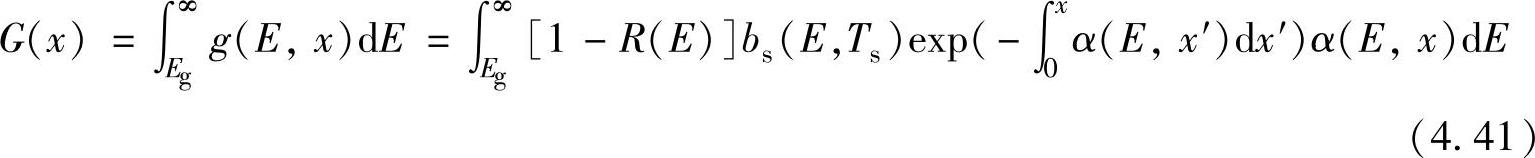
至此，得到了非平衡载流子的产生率与吸收系数的关系。

4.直接带隙半导体材料与间接带隙半导体材料吸收系数

根据偶极子近似理论可以得到直接带隙半导体材料吸收系数α与材料禁带宽度的关系，即

间接带隙半导体材料吸收入射光子时，必须伴随着声子的发射或者吸收才能实现跃迁。因此，量子跃迁在间接带隙材料中的要比直接带隙材料中的难许多，即间接带隙半导体材料吸收系数较直接带隙半导体材料小许多。对于间接带隙半导体，材料吸收系数α与材料禁带宽度的关系为

α（E）∝（E-E_g）² （4.43）

如果入射光子的能量很高，间接带隙半导体也可以发生无声子参与的直接跃迁，吸收系数会相对比较大。图4.5所示为Si、Ge和GaAs半导体材料吸收系数与波长的关系。

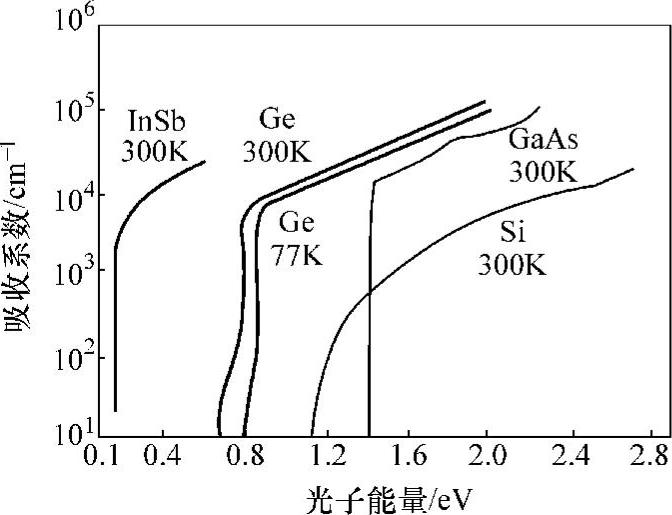
图4.5 Si、Ge和GaAs等半导体材料吸收系数与波长的关系

吸收系数是半导体材料一个非常重要的参量，根据吸收系数的大小可以确定太阳电池有源区的厚度，如GaAs材料的吸收长度约为1μm，这就意味着只需要1μm左右的厚度，就可以吸收入射光的70%以上。通常GaAs太阳电池有源区的厚度为3μm，几乎可以吸收99%以上的入射光。但是Si的吸收长度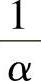大约是数十μm，所以为了更好地吸收入射光，单晶硅太阳电池一般做到一百甚至数百μm的厚度^[10]。