准热平衡状态下载流子的电流特性分析

若要知道准热平衡状态载流子的电流，必须得到修正后载流子分布函数的具体表达式。玻尔兹曼方程是非平衡分布函数所满足的一个方程，求解此方程可得到f_C（k，r）和f_V（k，r）的具体表达式。

准热平衡状态下，t时刻，在（r，k）处的电子一定是从（t-dt）时刻，从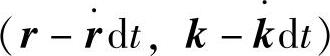漂移而来的，即^[4]

同样，碰撞使分布函数f发生改变，散射项写成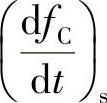，则

根据微分定义式可得

在稳态外场的作用下，分布函数随时间变化较小，所以

式（3.71）进一步简化为

式中等号左边代表散射项，右边代表由温度梯度和外场引起的漂移项。式（3.74）即为稳态外场作用下，电子气体系统的玻尔兹曼方程。

由式（3.68）可知

由于：

1）电子速度，；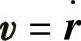

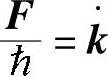2）在准热平衡状态，电子分布函数偏离热平衡状态分布不大，即

f_C（k，r）-f₀＜＜f₀ （3.75）

则

式（3.74）进一步修正为(www.xing528.com)

现采用弛豫时间近似理论，假定撤掉外场，经过时间τ后，分布函数由准热平衡状态f_C弛豫回热平衡状态f₀。

式中负号表示该过程与散射过程互为逆过程，τ是载流子的寿命。

此时式（3.79）进一步推导为

又因为导带电子受力F=-_rE，所以式（3.80）简化为

进一步求得

对比式（3.82）和（3.68），得到非对称函数f_A（k，r）为

将式（3.83）代入

得到电子电流与准费米能级的关系式为

J_e（r）=μ_enEⁿ_F （3.85）

从此_r=，其中

同理，空穴电流为

J_h（r）=μ_hpE^p_F （3.87）

则通过半导体内任一点的电流J（r）为^[1，2，41]