探讨能量状态密度的应用价值

根据量子理论，在宽度为L的势阱中，相邻能级的波矢k之差为

在以k_x，k_y，k_z为坐标轴的三维波矢空间，每个许可的量子态在波矢空间内的体积为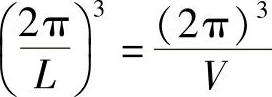，则单位体积内包含的量子态的数目为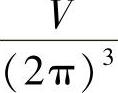。图3.8所示为k空间中的单电子许可态与能量为E_F的费米面^[16]。

所以，k～k+dk的体积元内的量子态数目为

对于三维空间，等能面为球面，从k～k+dk的体积元的体积为

dk=4πk²dk （3.16）

根据泡利不相容原理，每个量子态可以容纳两个自旋相反的电子。因此，k～k+dk的体积元内的电子态数目为

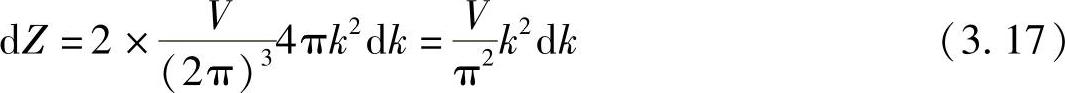
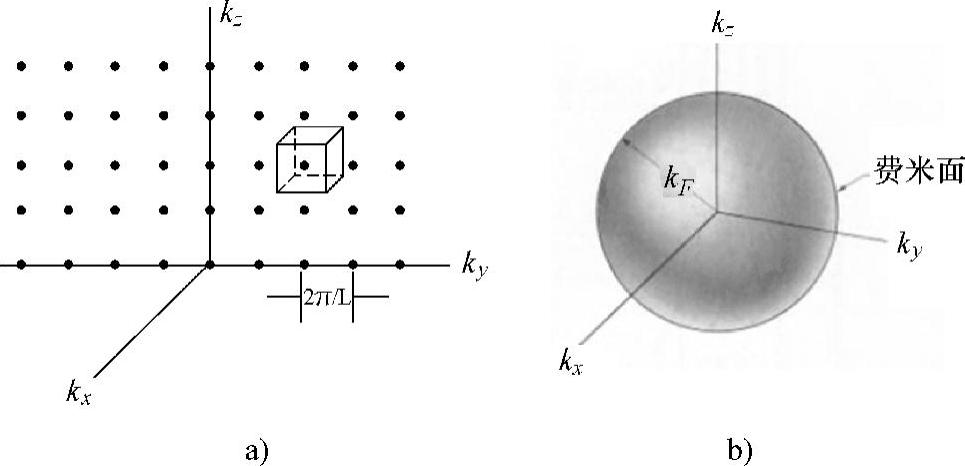
图3.8 波矢空间中的单电子许可态与能量为E_F的费米面

a）k空间中的单电子许可态 b）能量为E_F的费米面

（图3.8a中仅画出了k_yk₂平面上的一部分，每个量子态占据的k空间体积为）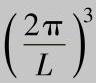

假设导带底E_C出现在k=0，根据式（3.2）对抛物线形能带近似得到能量E～E+dE之间的状态数为

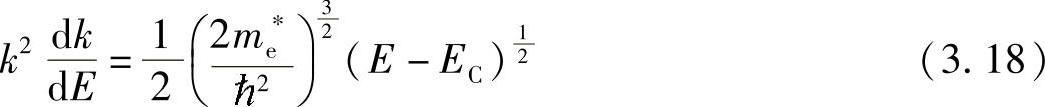(www.xing528.com)

得到单位晶体体积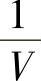内，单位光谱dk或单位能量dE的电子态数量，即状态密度分别可表示为

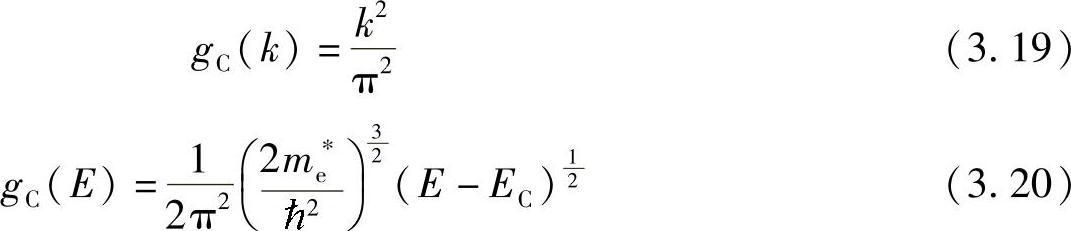
式中，g_C（k）的量纲为1；g_C（E）的量纲为cm^-3eV^-1。相比关于波矢k的状态密度g（k），关于能量E的状态密度应用更加方便。g_C（E）是一个双重密度，反映了单位能量、单位体积内的量子态密度，对能量E积分，得到在一定能量范围内电子量子态的数量。

同理，假定价带顶也出现在k=0，则根据式（3.6），可以得到价带的空穴状态密度（g_V，cm^-3eV^-1）为

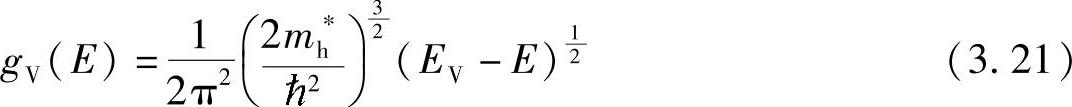
注意，式（3.20）和式（3.21）主要是针对各向同性的三维晶体材料，而对各向异性的材料并不适用。

二维量子阱太阳电池、一维量子线太阳电池和零维量子点太阳电池，电子的运动被束缚在一定方向上。对二维量子阱来说，k空间等能面为圆环，所以

dk=2πkdk （3.22）对一维量子线来说，k空间存在两个等能点，所以

dk=2dk （3.23）然后依据同样的方法进行推导，可以得到二维和一维半导体材料导带底部电子的状态密度g_2D（E）和g_1D（E）分别为^[15]

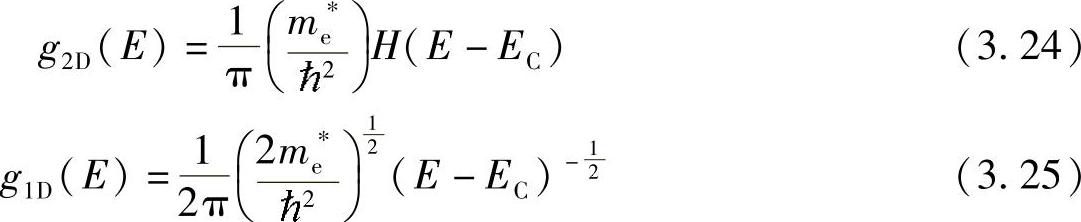
式中 H（E-E_C）——单位阶跃函数，满足

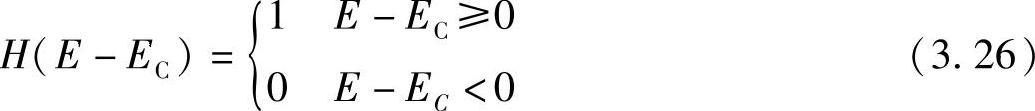
g_1D（E）反映了单位长度、单位能量间隔内的电子态数量；g_2D（E）反映了单位面积、单位能量间隔内的电子态数量。

在波矢空间中，实际半导体材料的电子或空穴能量曲线在远离导带底E_C或价带顶E_v的能带不满足抛物线形能带近似，因此这些能带的状态密度不适用上式。