薛定谔方程与布洛赫波分析

由能带理论可知，晶体中导带电子和价带空穴的运动可以由薛定谔方程描述^[11]为

式中 φ（k，r）——布洛赫波函数；

k——波矢；

r——空间位置矢量；

m——电子质量；

V（r）——晶体的周期性势场。

通过求解薛定谔方程，得到导带底电子的能量表达式为^[11]

式中 k_c——使电子能量曲线E（k）达到最小值的导带底（E_c，eV）波矢，可能k_c=0，也有可能不在k_c=0，这与晶面、晶向的方向有关；m^*_e——导带的电子有效质量，其单位与质量一样，由能带结构定义：

导带电子的速度（v_e，cm/s），即群速为

根据电子的准经典运动理论，导带电子的准动量（p，kg·cm/s）为

p_e=m^*_ev_e=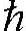（k-k_c） （3.5）(www.xing528.com)

但它并不代表半导体中电子的动量，但是在外力作用下，由于它的变化规律和导带电子的动量变化规律相似，所以有时称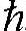k为半导体中电子的准动量。

同理，价带空穴的能量曲线最小值在价带顶（E_v，eV），而电子在价带顶E_v的能量最大。根据抛物带近似理论，得到价带空穴的能量曲线为^[12]

式中 k_v——使空穴能量曲线E（k）达到最小值的价带顶波矢（cm^-1）；

m^*_h——价带的空穴有效质量（kg）为

空穴有效质量m^*_h和电子有效质量m^*_e合称有效质量m^*。

价带空穴的速度为

价带空穴的准动量为

p_h=m^*_hv_h=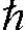（k-k_v） （3.9）

一般而言，导带底部电子的能带曲线和价带顶部空穴的能带曲线的曲率不同，所以电子有效质量m^*_e和空穴有效质量m^*_h也不相等。