干涉测量的基本原理与应用

干涉技术和干涉仪在光学测量中一直占有重要的地位。随着20世纪60年代激光器问世以及70年代半导体电子技术的发展，出现了激光干涉仪与微型电子计算机的结合，把干涉测量技术推向了新的水平。以干涉法测光学量为例，光学玻璃折射率的测量不确定度达10−6，应力双折射的测量不确定度达1nm，光学球面曲率半径的测量不确定度达1μm，光学薄膜厚度的测量不确定度达0.1nm，光学平面面形的测量不确定度达0.01λ，光学系统波像差的测量不确定度达0.05λ。由于在干涉仪中使用了激光器、新型光电器件和微型电子计算机，干涉测量不仅有很高的灵敏度和准确度，而且扩大了测量范围，在精密测量、精密加工和实时测控的诸多领域中均获得广泛的应用。

按光波分光的方法，干涉仪有分振幅式和分波阵面式两类，光学测量常用的是分振幅式。按用途又可将干涉仪分为两类，一类是通过测量干涉场上指定点的干涉条纹移动数或光程差变化量，进而求得试样的尺寸大小、位移量和物质折射率等；另一类是通过测量被测波面与参考标准波面产生的干涉条纹的变形量或条纹分布，进而求得试样表面微观几何形状、气流密度分布和光学系统波像差等。

干涉测量是基于光波叠加原理，在干涉场中产生亮暗交替的干涉条纹，通过分析处理干涉条纹来获取被测量的有关信息。

当两束光满足频率相同、振动方向相同以及初相位差恒定的条件，两束光就会发生干涉现象。在干涉场中任一点的合成光强为

式中，Δ为两束光到达某点的光程差；I1，I2分别为两束光的光强；λ为光波长。

干涉条纹是光程差相同点的轨迹，以下两式分别为亮纹和暗纹方程：

式中，m为干涉条纹的干涉级。

干涉仪中两支光路的光程差Δ可表示为

(www.xing528.com)

式中，ni，nj分别为干涉仪两支光路的介质折射率；li，lj分别为干涉仪两支光路的几何路程。

当把被测量引入干涉仪的一支光路中，干涉仪的光程差则发生变化，干涉条纹也随之变化。通过测量干涉条纹的变化量，可以获得与介质折射率n和几何路程l有关的各种物理量和几何量。

为了获取明亮、清晰和稳定的干涉条纹，在测量中需要采取保证良好干涉条件的一些技术措施。

在光学车间广泛使用玻璃样板来检验球面（包括平面）光学零件的面形偏差，GB 2831—81规定了光圈的识别方法。它具体包括下列三项：

（1）半径偏差N，即被检光学表面的曲率半径相对参考表面曲率半径的偏差。此偏差以所对应的光圈数N表示，如图6−1（a）～（d）所示面形偏差较大N≥1的情况，是以有效检验范围内直径方向上最多干涉条纹数的一半来度量光圈数N。在面形偏差较小N＜1的情况下，光圈数N以通过直径方向上干涉条纹的弯曲量h相对于条纹的间距H的比值N来度量，即，如图6−1（e）所示。

（2）像散差Δ1N，即被检光学表面与参考光学表面在两个相互垂直方向上的光圈数不等所对应的偏差。此偏差对应的光圈数用Δ1N表示。Δ1N是以两个相互垂直方向上干涉条纹数（Nx，Ny）的最大代数差的绝对值来度量。图6−1（f）表示椭圆形像散差，Nx=2，Ny=3，偏差方向相同，如图6−1（g）所示马鞍形像散差，Nx=−1，Ny=2，偏差方向相反，Δ1N=；如图6−1（h）所示柱形像散差，在某一方向上干涉条纹数为0（Ny=0），Δ1N就取决于Nx值。当Nx≠Ny，Nx和Ny又都小于1时，根据两个方向干涉条纹的弯曲度来确定Nx和Ny；如图6−1（i）所示，Nx=0.2，Ny=0.4，则Δ1N=0.2。

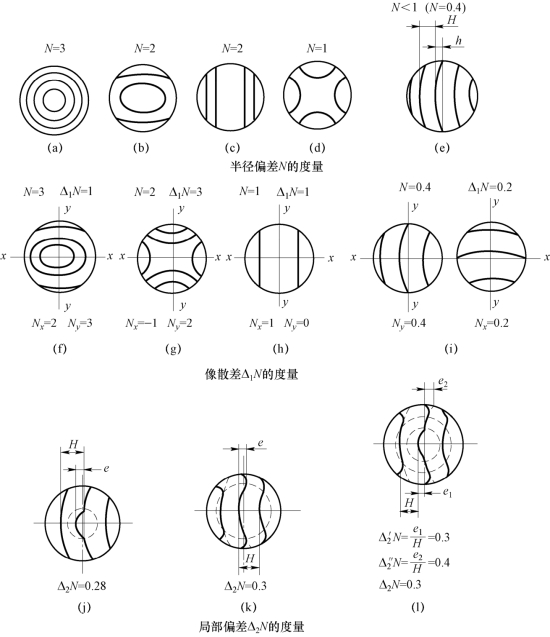
图6−1　面形偏差的度量

（3）局部偏差Δ2N，即被检光学表面与参考光学表面在任一方向上产生的干涉条纹的局部不规则程度。此偏差所对应的干涉条纹数用Δ2N表示。Δ2N以局部不规则干涉条纹相对理想平滑干涉条纹的偏离量e与两相邻条纹间距H的比值来度量，即。如图6−1（j）所示为中心局部不规则偏差；如图6−1（k）所示为边缘局部不规则偏差；如图6−1（l）所示为中心及边缘均有局部偏差，应分别求出并取大值来表征。

值得指出，半径偏差N在一定程度上会使光学成像关系、像面和放大倍率等产生微量变化，但这些变化可经适当调整各光学零件间的相对位置而得到一定程度的补偿。而光学零件的面形不规则引起的像散偏差Δ1N和局部偏差Δ2N，则将直接影响到光学系统的成像质量，这种影响一般是难以补偿的。