衍射受限系统的分辨率探讨

在光学系统（即无像差理想光学系统）中，由于光的衍射，一个发光点通过光学系统成像后得到一个衍射光斑，两个独立的发光点通过光学系统成像得到两个衍射光斑。通过考察不同间距的两发光点在像面上两衍射像可被分辨与否，就能定量地反映光学系统的成像质量。作为实际测量值的参照数据，应了解衍射受限系统所能分辨的最小间距，即理想系统的理论分辨率数值。两个衍射斑重叠部分的光强度为两光斑强度之和。随两衍射斑中心距的变化，可能出现如图3−29所示的几种情况。当两发光物点之间的距离较远，两个衍射斑的中心距较大时，中间有明显暗区隔开，亮暗之间的光强对比度k≈1，如图3−29（a）所示；当两物点逐渐靠近时，两衍射斑之间有较多的重叠，但重叠部分中心的合光强仍小于两侧的最大光强，即有对比度1＞k＞0，如图3−29（b）所示；当两物点靠近到某一限度时，两衍射斑之间的合光强将大于或等于每个衍射斑中心的最大光强，两衍射斑之间无明暗差别，即对比度k=0，两者“合二为一”，如图3−29（c）所示。

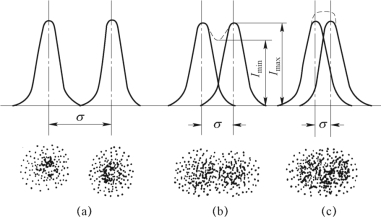
图3−29　两衍射斑中心距不同时的光强分布曲线和光强对比度

（a）中心距σ等于中央亮斑直径d；（b）σ等于0.5d；（c）σ等于0.39d（ka=1，kb=0.15，kc=0）

人眼观察相邻两物点所成的像时，要能判断出是两个像点而不是一个像点，则起码要求两衍射斑重叠区的中间与两侧最大光强处要有一定量的明暗差别，即对比度k＞0。k值究竟为多大时人眼才能分辨出是两个像点而不是一个像点？这常常因人而异。为了有一个统一的判断标准，瑞利（Rayleigh）认为，当两衍射斑中心距正好等于第一暗环的半径时，人眼刚能分辨开这两个像点，如图3−30所示。根据式（3−54）可求出这时两衍射斑的中心距为

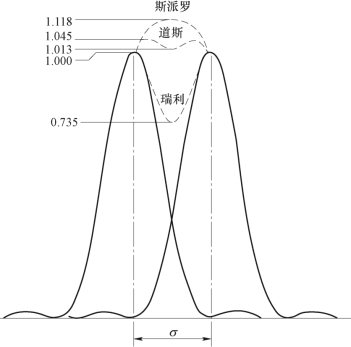
图3−30　三种判据的部分合光强分布曲线

这就是通常所说的瑞利判据。

按照瑞利判据，两衍射斑之间光强的最小值为最大值的73.5%，人眼很易察觉，因此有人认为该判据过于严格，于是提出了另一个判据——道斯（Dawes）判据，如图3−30所示。根据道斯判据，人眼刚能分辨两个衍射像点的最小中心距为

按照道斯判据，两衍射斑之间合光强的最小值为1.013，两衍射中心附近的光强最大值为1.045（设单个衍射斑中心最大光强为1）。

还有人认为，当两个衍射斑之间的合光强刚好不出现下凹时为刚可分辨的极限情况，如图3−30所示。这个判据称为斯派罗（Sparrow）判据。根据这一判据，两衍射斑之间的最小中心距为

两衍射斑之间的合光强为1.118。(www.xing528.com)

图3−31给出了上述三种判据的三维合光强分布。

实际工作中，由于光学系统的种类不同、用途不同，分辨率的具体表示形式也不同。例如，望远系统，由于物体位于无限远，所以用角距离表示刚能分辨的两点间的最小距离，即以望远物镜后焦面上两衍射斑的中心距σ0对物镜后主点的张角α表示分辨率：

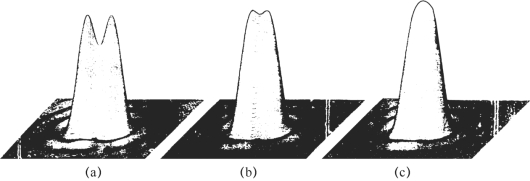
图3−31　瑞利、道斯和斯派罗判据的三维合光强分布

照相系统以像面上刚能分辨的两衍射斑中心距的倒数表示分辨率：

在显微系统中则直接以刚能分辨开的两物点间的距离表示分辨率：

式中，β为显微物镜的垂轴放大率。

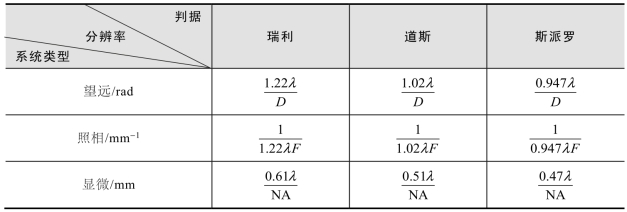
表3−6列出了不同类型的光学系统按不同判据计算出的理论分辨率。表中D为入瞳直径（mm）；NA为数值孔径；应用于白光照明时，取光波长λ=0.55×10−3mm。

表3−6　三类光学系统的理论分辨率

以上讨论的各类光学系统的分辨率公式都只适用于视场中心的情况。对望远系统和显微系统而言，由于视场很小，只需考虑视场中心的分辨率；对照相系统，由于视场通常较大，除考虑视场中心的分辨率外，还应考虑中心以外视场的分辨率。