焦距的光电法测量技术优化方案

传统的光学系统光学参数测量方法是由测量人员在光具座上逐项进行观测、记录、数据分析和计算结果等一系列工作，存在效率低、精度不稳定、对测量人员要求高等缺点。这里描述的是一种新的测量方法，即用光电法和数字图像处理方法测量光学系统的焦距。这种方法的思路是：用液晶屏显示分划图形取代平行光管的分划板（玻罗板），通过平行光管形成一个无穷远的目标，由CCD摄像机及采集卡采集该目标通过被测系统所成的像，形成数字图像输入计算机。然后进行数字图像处理和分析，并结合已知的分划图形的参数计算出被测系统的光学参数。用液晶屏显示分划图形取代传统的玻璃分划板，可以避免频繁更换分划板，对其他参数测量时若需改变分划图形将会十分方便。

1.光电法测量的原理及实验装置

系统的整体结构可以用图3−15来表示。从图中可以看出，计算机是整个系统的核心部件，发生目标图形、数字图像的分析和处理以及计算结果都由它来控制或执行。实验中，CCD靶面垂直光轴置于被测光学系统的焦平面上，液晶屏置于平行光管物镜焦平面上。这样，“无穷远处”的目标图形经被测系统成像在CCD靶面上，经图像采集卡形成数字图像送入计算机进行分析。

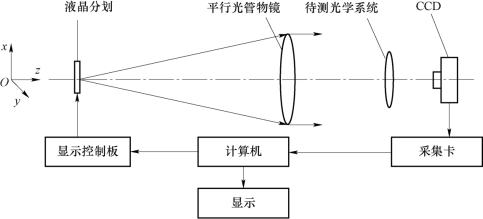
图3−15　总体结构图

本实验中，液晶显示屏采用夏普的LM64P11，平行光管物镜焦距，CCD采用敏通的MTV−3012。

2.数学模型建立和算法原理

（1）基本测量公式。

传统的方法中用放大率法测量焦距时是通过测量被测光学系统对玻罗板所成的像上的线对间距计算出被测光学系统的焦距的。但是对于由CCD和采集卡得到的数字图像，一般来说图像上的某一点并不严格对应着CCD靶面上的某个像素，因此很难通过数字图像上的线对直接计算CCD靶面上的实际像的线对间距。所幸的是，尽管如此，这两种线对的间距仍然呈现着一种比例关系，而且这种比例关系是固定的。因此，我们就有希望通过一个已知焦距的标准透镜来确定待测光学系统的焦距。

图3−16表示了分划图形、CCD靶面上的实际像和采集到的数字图像之间的关系。当分划图形是间距为y的一对平行线时，CCD靶面上得到的实际像是一对间距为y′的平行线，而数字图像上也得到一对平行线，其间距用这两条平行线间垂直距离上的相当像素数p来表示，它的单位不是mm，而是pixels（像素数）。p和y′之间存在一个比例系数r，而且有

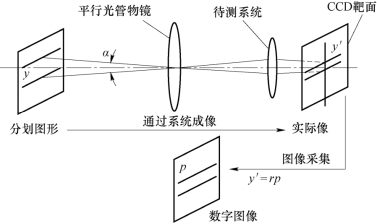
图3−16　数字图像和实际像的对应关系

若用w表示液晶屏的像素宽度，m表示分划图形线对间所含液晶像素数，则根据放大率法原理，透镜焦距f′可表示为

是一个常数，而p的值可以借助于数字图像分析和处理精确地得到。利用焦距标准透镜（下标std表示标准透镜）标定C0后，对于不同的光学系统就可以根据p计算出焦距f′。

（2）求取p。

这种测量方法对作为分划图形的两条平行线的要求很低，只要求直线具有一定的宽度，而不是很细；而且对平行线的方向和间距都没有严格的要求，只需要使数字图像上的直线大致呈水平方向以方便处理即可。于是数字图像上就得到了两条具有一定宽度和灰度分布的平行直线。只要确定这两条直线的中心线就可以得到它们之间的距离p了。数字图像可以认为是一个灰度值分布矩阵，该矩阵的每一列上都有两处因为平行直线经过而造成的灰度值明显比背景灰度值低。用重心法求出这两处的重心点，作为直线的中心经过该列的位置。每一列都可以得到两个这样的重心点，所有的重心点大致排成两行。以此可以拟合得到两条平行线，进而求出间距p。

（3）重心法求中心点。

通过求平均值的方法可以有效地降低随机噪声的影响。采集n幅图并求平均，随后的操作都是针对这幅平均图像进行的，并且是将数字图像作为灰度值矩阵来计算的。图3−17所示是平均图像中扫描一列得到的该列灰度值分布示意图。其中，图（a）是10幅图平均以后的图像，图（b）是图（a）中第50列的灰度值分布折线图，折线图中的水平坐标表示各点在该列中的位置，垂直坐标表示各点的灰度值。为方便图像处理和减小背景的噪声影响，可选定阈值TH为最大与最小灰度值的中间值（设最大和最小灰度值分别为gmax和gmin，则有TH=gmax−0.5（gmax−gmin）），将灰度值矩阵中大于TH的值都置零。图3−17（c）所示就是经过阈值处理后的第50列的灰度值分布折线图。这样处理后，矩阵中的各列向量rs（下标s表示第s列）只有在直线经过该列的地方有非零值，rs表示为

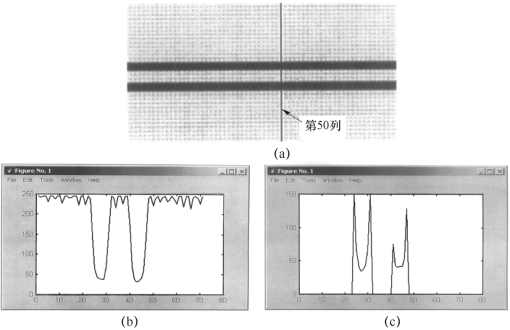
图3−17　平均图像中扫描一列得到的该列灰度值分布

（a）10幅图平均以后的图像；（b）图中第50列的灰度值分布；（c）将灰度值大于阈值的点都置零后第50列的灰度值分布

其中，ak，ak+1，…，ak+u，aj，aj+1，…，aj+v是rs中不为零的元素。设这一行中的左右两个不等于零的区域的重心点坐标分别为Ls（XL，YL）和Rs（XR，YR）。用下面的式子求得以像素数为单位的坐标值：

对每一行重复进行上面的计算，就得到大致排成两行的两个点集L1和L2。

（4）拟合平行直线并求取p。

图像上的两条直线应该是平行的，因此把这两条平行直线一起参与最小二乘拟合，得到各条直线的方程，这样既符合实际情况，也能保证拟合出来的直线的斜率是相等的，有利于后续数据处理。这里，参与拟合的直线数为2；各条直线参与拟合的点数相等，为n；各直线的点集为L1、L2。设各直线方程为

利用最小二乘法，构造如下目标函数：(www.xing528.com)

有了k、b1和b2，就可以用下面的式子求出间距p：

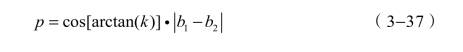
3.标定C0

对于任一个焦距标准透镜都可以计算出常数C：

C的相对标准不确定度为

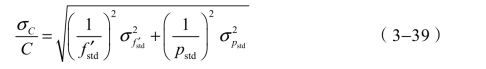
可见对于不同焦距的标准透镜，得到的C的相对标准不确定度是不同的，故使用多个标准透镜进行不等精度测量来标定C0。设CCD摄像机靶面到透镜像方主面的距离为z，分划线对对平行光管物方主点的张角为α，根据式（3−30）有，由此可以得出p的相对精度等于定焦的相对精度。

如图3−18所示，当一个像点在CCD摄像机靶面上的弥散斑小于一个像素时，得到的数字图像是清晰的；当弥散斑大于一个像素时，图像就变得模糊。由于分划线基本呈水平方向，在图像处理时是在垂直方向上进行扫描的，因此图像在垂直方向上清晰的时候就认为完成定焦。MTV−3012型CCD摄像机靶面垂直方向上的像素宽度加上两条隔离带的总宽度为0.008mm。定焦精度可用下面的式子表示，其中D是透镜的通光口径。

图3−18　定焦精度示意图

由于，所以有

的相对标准不确定度可达到0.001，于是C的相对标准不确定度为

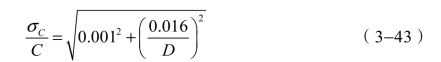
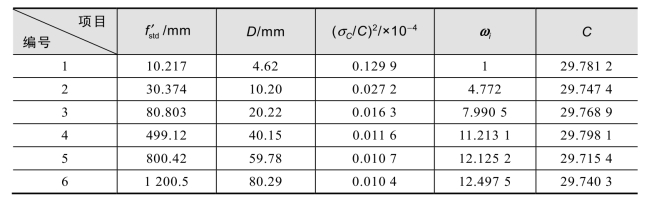
可见，不同的，C有不同的相对标准不确定度。取权重ωi为相对标准不确定度平方的倒数，并归一化。不同的的数据如表3−3所示。

根据公式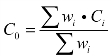，得到C0=29.753 4。

表3−3　各个标准透镜的相关数据

4.误差分析

根据式（3−30），并利用间接测量误差的传递关系式，可得到焦距的相对标准不确定度：

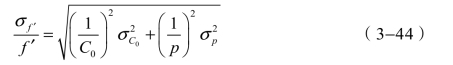
加权算术平均值的相对标准不确定度：

再联系式（3−40）和式（3−42），便可得到f′的相对标准不确定度计算式：

若D=5mm 或10mm，则=0.33%和0.2%；当D大于30 mm时，相对标准不确定度小于0.07%。

以上分析说明，误差主要来自式（3−46）中的第二项，即定焦精度。使用像素尺寸更小的CCD，还可以提高测量精度。