望远镜和显微镜的对准及调焦误差分析

人眼通过望远镜和显微镜去对准和调焦是为了提高对准与调焦的准确度。

1.对准误差

（1）望远镜的对准误差。

如图3−2（a）所示，设人眼直接对准时的对准扩展不确定度为δ，望远镜的放大率为Γ，通过望远镜观察时物方的对准不确定度设为γ，则有如下关系：

例 1 V棱镜折光仪的望远镜放大率Γ=6×，入瞳直径D=12 mm，对准方式是夹线对准，其扩展不确定度，则望远镜对准的扩展不确定度为

（2）显微镜的对准误差。

如图3−2（b）所示，设显微镜的总放大率为Γ，其中物镜的垂轴放大率为β。通过显微镜观察时物方的对准扩展不确定度设为Δy，则有

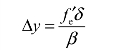
式中，为目镜焦距。

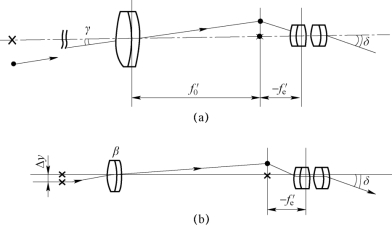
图3−2　望远镜和显微镜的对准误差

因为，故得

式中，250为人眼的明视距离，mm；δ为人眼的对准扩展不确定度，rad。

例如，假设一个V棱镜折光仪的显微镜放大率Γ=58×，显微物镜的数值孔径NA=0.15，对准方式是夹线对准，则可以算出，显微镜物方的对准扩展不确定度为

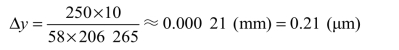
又如，假设一个经纬仪的度盘刻划圆直径D=270 mm，用游标对准方式读数，即δ=0.25′，要求由对准误差带入经纬仪测角误差的部分不大于假设显微镜物方的对准扩展不确定度为Δy，则与Δy对应的测角扩展不确定度为

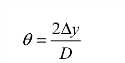
根据式（3−8）消去Δy，即得计算放大率的公式为

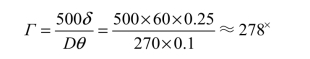
（3）对准误差与分辨率的关系。

由式（3−7）和式（3−8）可以看出，对准误差与放大率Γ成反比。是否可以认为，只要单纯增大Γ，对准误差必然减小呢？实践证明，对准误差的减小还受到光学仪器分辨率的限制。因为即使光学仪器的像质优良，对准误差和分辨率也都存在着目标经物镜成像的清晰度受衍射影响这一因素，所以两者有一定的联系。

实验结果：像质优良的望远镜和显微镜的单次测量对准不确定度最小只能达到它的理论分辨率的1/6～1/10，即

式中，D为望远镜的入瞳直径；NA为显微物镜的数值孔径。当取λ=0.56μm 时，

用式（3−9）去检查前面V棱镜折光仪的两个例子。望远镜入瞳直径D=12 mm，则理论分辨率，前面已算出，说明实际可以达到的对准准确度。

显微物镜的数值孔径NA=0.15，，前已算出Δy=0.21μm，而（对扩展不确定度建议用1/6，标准不确定度才用1/10）。故显微镜的对准扩展不确定度最好也只能达到0.33 μm，对应标准 不确定度为

2.调焦误差

（1）望远镜的调焦误差。

计算望远镜的调焦误差常用清晰度法和消视差法。

清晰度法 将人眼的两部分调焦误差，如式（3−1）和式（3−2）所示，分别换算到望远镜物方，即可求出望远镜用清晰度法调焦的扩展不确定度。

设在望远镜像方的调焦扩展不确定度为时，对应于物方为。应用牛顿公式xx′=ff′，不难求出

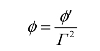
由此可得，在望远镜物方

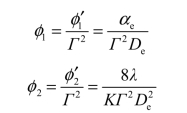
当眼瞳直径De大于望远镜的出瞳直径D′时，以实际有效的像方通光孔径代替公式中的De，则上二式变为

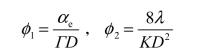
式中，D为望远镜的入瞳直径。

若D′＞De，则ΓDe为实际有效的入瞳直径，即应以ΓDe代替式中的D。

望远镜的调焦扩展不确定度为

标准不确定度为

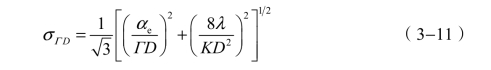
消视差法 人眼通过望远镜调焦时，眼睛在出瞳面上摆动的最大距离将受到出瞳直径的限制。因为在视网膜上像的位置由进入眼瞳的成像光束的中心线与网膜的交点决定，因此眼瞳的有效移动距离不等于眼瞳的实际移动距离t，而等于出瞳中心到进入眼瞳的光束中心的距离b，如图3−3（a）所示。图中阴影线部分表示进入眼瞳的光束截面积。不难看出，b越大进入眼睛的光束越细，像越暗，眼睛的对准准确度将越低。一般规定，当De=2mm 左右时（这时视场亮度约为2×104cd/m2），计算调焦误差的眼睛最大移动距离是眼瞳中心移至出瞳边缘处［如图3−3（b）所示］，这时

在实验室条件下，视场亮度有时达不到要求的2×104cd/m2的水平，De将增大。但当De≤3mm 时（视场亮度大于100 cd/m2），只要保持进入眼瞳的光束截面积基本不变［与De=2mm 时，图3−3（b）的画斜线的面积基本相同］，对准准确度就不会有明显下降，因此上式中的可看作定值1/2 mm，公式变为

将式（3−5）的换算到望远镜物方得

将式（3−12）代入上式，得调焦扩展不确定度为

(www.xing528.com)

单次测量的标准不确定度为

式中，δ由表3−1查出，但单位改用“rad”。

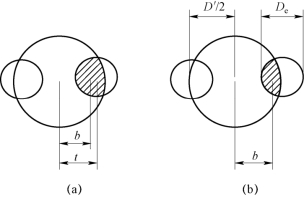
图3−3　眼瞳在出瞳面上摆动时的有效移动距离

例如，假设要校正一个平行光管的分划板位置，要求分划板位于平行光管物镜的焦面上。设平行光管口径Dc=50 mm，物镜焦距。用一个望远镜对向平行光管，观察它的分划板像，当看到这个像与望远镜的分划板刻线同样清晰和消视差时，则认为平行光管已校正好。设望远镜入瞳直径DT=100 mm，物镜焦距，放大率Γ=40×，则可求出相应的调焦误差。

① 用清晰度法并观察时，实际通光口径D=50 mm=0.05 m，取αe=2′=2/3438（rad），λ=0.56μm=0.56×10−6m，代入式（3−10）得

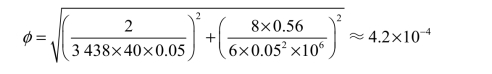
② 用消视差法并设对准方式是压线对准，取δ=1′，眼瞳直径De=2mm，，代入式（3−13）得

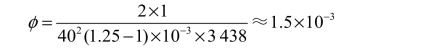
（2）显微镜的调焦误差。

计算显微镜的调焦误差常用清晰度法和消视差法。

清晰度法 将人眼的调焦误差换算到显微镜物方的简单方法，是把显微镜看作一个放大率较大的放大镜，其等效焦距为

式中，Γ为显微镜总放大率。

显微镜物空间的折射率为n时，设人眼调焦不确定度为，则由式（3−1）和牛顿公式可知，显微镜物方对应的调焦不确定度为

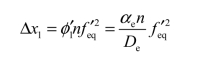
若De大于出瞳直径D′，则上式变为

由显微镜的出瞳直径D′与数值孔径NA及总放大率Γ的关系（如图3−4所示），得

代入式（3−15）得

由物理焦深产生的调焦不确定度，也可通过较简单的方法求得。

如果De＞D′，则当目标像和标志像发出的光束在显微镜出瞳范围内所截波面之间的波差小于时，人眼看到二者同样清晰。假定显微镜像质良好，在目标像到标志像的深度范围内波像差的变化很小，那么在显微镜物方，目标和标志对入瞳的波差也应小于（λ为真空中的波长）。

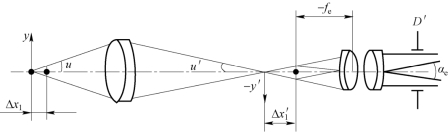
图3−4　显微镜的几何焦深Δx1与分辨角αe以及出瞳直径D′与孔径角u的关系

设波差达时，目标到入瞳的距离为R1，标志到入瞳的距离为R2，入瞳直径为D，则当NA≤0.50时，二者之间在显微镜入瞳处的波差可近似得

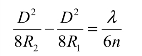
假设物空间介质的折射率为n，物方最大孔径角为U，而且差值R2−R1=Δx2是个很小的数，则有

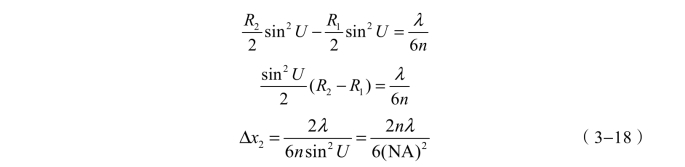
总的调焦扩展不确定度为

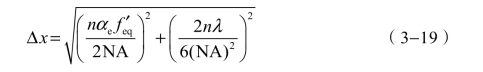
单次测量的标准不确定度为

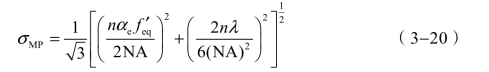
消视差法 求调焦误差的方法与求式（3−17）的方法相似。

将式（3−5）换算到显微镜物方得

将式（3−12）代入上式中，得调焦扩展不确定度为

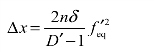
再应用式（3−16），最后得消视差法的调焦扩展不确定度为

单次测量标准不确定度为

例如，假设有一架显微镜，现在要确定其分划板的位置，显微物镜NA=0.25，β=10×，目镜Γe=10×，则可求出显微镜对分划板刻线面调焦的调焦扩展不确定度。

假如De=1 mm＜D′，则实际的数值孔径NA=0.20，这时Δx=5.0μm。

② 用消视差法。设被调焦的分划板刻有直线（线宽0.01 mm），显微镜的分划板上刻有叉线，故有δ=10′=0.17′。显微镜的出瞳直径为

设眼瞳直径De=2 mm。将上面各值代入式（3−22）得

根据式（3−10）、式（3−13）、式（3−19）和式（3−22），分析两种方法的调焦误差，可以得到如下结论：由于消视差法可通过选择有利的对准方式使对准误差δ大大减小，因此，系统出瞳直径D′≥2mm时，用消视差法准确度高；D′≤1mm 时，用清晰度法准确度高；1mm＜D′＜2mm 时，两种方法准确度相差不多。这个结论与实践结果基本吻合。

实际进行目视法调焦时，往往两种方法同时采用。首先调至目标与标志同样清晰，再左右摆动眼睛观察二者间有无视差，最后以“清晰无视差”定焦。