(1)两次傅里叶变换光学传递函数的计算。
由上面的讨论知道,子午传递函数OTFt(μ)和弧矢传递函数OTFS(ν)分别为

则由式(1−42)得

同理

式中

分别称为子午线扩散函数和弧矢线扩散函数。在实际计算中,它们不必由上式求出,而可以直接由光瞳函数求出。线扩散函数与光瞳函数的关系为

这样,用两次傅里叶变换法计算光学传递函数的基本步骤为:
计算光学系统的波像差W(Y,Z)。并确定光瞳函数的有效范围,即确定所选定的出瞳的形状,构造光瞳函数g(Y,Z),当然,这里假定A(Y,Z)≡1。
对光瞳函数g(Y,Z)按式(1−55)和式(1−56)进行傅里叶变换及积分运算,分别得到子午线扩散函数It(y′)及弧矢线扩散函数IS(z′)。
分别对It(y′)和IS(z′)作傅里叶变换,即可得到子午和弧矢光学传递函数OTFt(μ)和OTFS(ν)。实际上,上面三点可以归结为:求波像差、确定光束截面内通光域、确定傅里叶变换算法。
① 利用样条函数插值计算波像差。
前面已经讨论过了,无论是采用自相关法还是采用两次傅里叶变换法计算光学传递函数,都要首先计算光学系统的光瞳函数(1−46)。已经假定光束的通光面内振幅均匀分布,即A(Y,Z)≡1。这样,光瞳函数g(Y,Z)的计算实际上变为波差函数W(Y,Z)的计算及对实际光瞳函数的积分域(即所谓的光瞳边界)的确定。要提高光学传递函数的计算精度,首先要提高波差的计算精度,并精确地确定光束的通光区域。
通过在积分域内逐点计算均匀分布的各点对应的波差值可以计算出整个系统的波像差,但计算量太大。通常采用的方法是在光瞳函数积分面内计算若干条抽样光线的波差,然后用一个波差逼近函数去吻合,再利用此逼近函数计算出积分面内所需求和点的波差值。在波像差插值计算中,幂级数多项式是比较早且常用的波差插值函数。为了提高波差的插值精度,应该增加抽样光线的数量并提高多项式的次数,但高次多项式插值具有数值不稳定性,且插值过程不一定收敛。一般可以采用最小二乘法来确定用于波差插值的幂级数多项式,但当次数增大时,用于求解其系数的法方程组的系数矩阵往往趋于病态,而且即使在插值节点处也仍然存在误差。为此,人们尝试进行改进,如利用切比雪夫多项式和泽尼克多项式等。它们基底的正交性,使得多项式求解的法方程组的条件得到改善,从而提高了波差插值的精度。利用样条函数插值计算波像差也是一种很好的方法,通常采用三次样条函数来作为波像差插值函数。利用样条函数计算波像差的具体问题请参考有关书籍。
② 确定光束截面内通光域。
由于光栏彗差及拦光的影响,轴外视场的光束截面形状变得非常复杂。而通光域边界的计算精确与否,将直接影响到传递函数值的计算精度。为了提高光学传递函数的计算精度,有必要精确地确定出射光束截面内的通光域,也就是光瞳函数的积分域。对此,人们做过大量的工作,提出的方法大多是确定少量边界点,然后用近似曲线来拟合积分域的边界,如W.B.King提出的椭圆近似法及投影光瞳法。另外,还有分段二次插值法、最小二乘曲线拟合法等。在国内的程序中,采用确定较多的通光域的边界点,然后直接用折线拟合边界。
③ 利用快速傅里叶变换法计算光学传递函数。
利用常规的数值积分技术,用自相关法比用两次傅里叶变换法要快得多。自从Cooley−Tukey提出了傅里叶变换的快速计算方法(简称快速傅里叶变换,计为F.F.T)之后,则改变了这种状况。将快速傅里叶变换用于两次傅里叶变换法,通常只需自相关法所用时间的五分之一,使得两次傅里叶变换法计算光学传递函数变得实用化。根据前面的讨论,两次傅里叶变换法计算光学传递函数时,第一次傅里叶变换首先由光瞳函数求出子午和弧矢的线扩散函数,第二次傅里叶变换由线扩散函数求出子午和弧矢的光学传递函数。在计算机上进行傅里叶变换的过程请参考有关书籍。
(2)自相关法光学传递函数的计算。(https://www.xing528.com)
由前面的讨论,子午传递函数OTFt(μ)和弧矢传递函数OTFS(ν)分别为
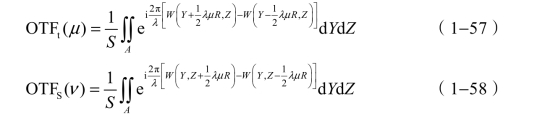
式(1−57)的积分域A如图1−36(a)所示,式(1−58)的积分域A如图1−36(b)所示。

图1−36 OTFt(μ)和OTFS(ν)的积分域
自相关法光学传递函数的计算程序大体上可以分为三个部分:
① 计算实际出瞳的形状。
实际光学系统中,轴外点的出瞳形状是比较复杂的,一般由两个或三个圆弧相交而成。光瞳形状可以用椭圆近似,也可以用阵列或者其他方法表示,但这些方法都比椭圆近似复杂得多,使用较少。
② 计算波像差函数。
波像差通常采用多项式的形式,由于共轴系统的对称性,波像差的幂级数展开式中应不出现Z的奇次项,级数中的各项应由(Y2+Z2)和Y来构成,我们取初级、二级和三级共14种像差,加上常数项共有15项,它们的具体形式为

实际光瞳的中心光线和像面的交点作为参考球面波的球心,参考球面波的半径等于像距L′。为了确定上面多项式中的15个系数,可采用计算抽样光线的方法,再利用最小二乘法求解。有了15个系数,波差函数W(Y,Z)就完全确定了。
③ 在出瞳归化成单位圆时的传递函数计算公式。
在计算波差函数时,把出瞳面上的坐标归化为单位圆,相当于前面传递函数计算公式中的瞳面坐标都除以实际出瞳半径hm,同时为了书写简化,设:

代入式(1−57)和式(1−58)以后,得到出瞳归化成单位圆的公式如下:
由于采用了椭圆近似,并把椭圆归化成为单位圆,因此无论是轴上或轴外点,积分区域永远为两个圆的相交部分。
对于弧矢传递函数来说,计算公式为

同理,也有
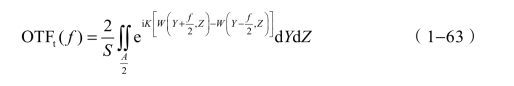
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




