几何像差和垂轴像差的图形分析

要了解一个系统的成像质量需要计算很多像差。为了对成像质量有一个全面的、明确的认识，我们把前面计算的各种像差数据画成曲线。下面就以第1.7节的双胶合物镜为例，来说明一些常用的像差曲线。

（1）轴上点的球差和轴向色差曲线。

把种像差曲线做在同一张图中，纵坐标代表归化的孔径h，横坐标代表球差δL′，如图1−25所示。从图中可以看出3种不同颜色的球差曲线随孔径的变化情况，也可以看出轴向色差的大小，C和F光线曲线沿横轴方向的位置之差就是轴向色差。根据这3条曲线就可以了解轴上点的成像质量。

（2）正弦差（相对彗差）曲线。

如图1−26所示，纵坐标代表孔径h，横坐标代表正弦差SC′，根据1.7节的输出结果可以做出曲线。前面曾经指出，物点在近轴区域内，也就是小物体，用大孔径光束成像时，除了有球差和轴向色差外，还有彗差，通常用相对彗差即正弦差表示。正弦差曲线，加上球差和轴向色差曲线，就代表了光轴附近也就是像面中心附近区域的成像质量。

图1−25　轴上点球差和轴向色差曲线

图1−26　正弦差曲线

（3）畸变和垂轴色差曲线。

畸变和垂轴色差都是与主光线有关的像差，因此我们也把它们做在同一张图上，如图1−27所示。横坐标代表，纵坐标代表视场ω，同样按归化视场分划。从图中可以看出每种颜色光线的畸变随视场变化的情况，同时可以看出垂轴色差的大小，F和C光线曲线沿横轴方向的位置之差就是垂轴色差。需要注意的是，3条曲线都过原点，这是因为当视场为0时，任何颜色光线均没有畸变。

（4）细光束像散曲线。

细光束像散表示主光线周围细光束的聚交情况，。如图1−28所示，横坐标为，纵坐标为视场ω。图中t代表子午细光束场曲，s代表细光束弧矢场曲。如果除中心谱线外，还计算了其他2种色光的像差，则t和s各有3条，分别对应D，F和C 3种颜色光线的。需要注意的是，当视场为零即ω=0时，系统没有像散（轴上点只有球差和轴向色差），所以和应交于一点，也就是理想像点处。因此各色光0视场的和应交于各自的理想像点处，D光的理想像平面就是过坐标原点的平面，所以D光0视场的应过原点，F和C光线的理想像点与D光的不重合，所以F和C光线0视场的不过原点，其交点与原点的距离恰好就是F光和C光的0孔径轴向球差。

图1−27　畸变和垂轴色差曲线

图1−28　细光束像散曲线

畸变和垂轴色差代表了主光线的像差，再加上细光束像散曲线就表示了主光线周围细光束（也就是核心光束）部分的像差。但是实际成像光束必须有一定大小，否则成像太暗。成像光束有一定宽度，就会有宽光束像差。下面讨论轴外点宽光束的像差曲线。

（5）轴外点子午球差和子午彗差曲线。

上面所讨论的像差都只与孔径或视场中的一个量有关，而轴外点的宽光束像差则与孔径和视场两个量都有关。如图1−29和图1−30所示，我们画出3个孔径（1h，0.707 1h，0.5h）的轴外点子午球差和子午彗差的曲线。

纵坐标代表视场ω，横坐标代表和。第1.5节的输出数据中只给出了1ω，0.85ω，0.707 1ω，0.5ω和0.3ω 5个视场的和，没有给出0视场的和，那么曲线和横坐标应交于何处呢？当视场为0时，不同孔径光线的子午和弧矢彗差都为0，子午球差就是轴上点相应孔径高度处的球差。因此，图1−30中各孔径的曲线应过原点，而图1−29中各孔径的曲线与横坐标的交点应分别等于各自的轴上点相应孔径的球差值。

图1−29　子午球差曲线(www.xing528.com)

图1−30　子午彗差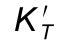曲线

在图1−29中，3条曲线基本平行，几乎与横坐标垂直，说明子午球差随视场变化不大。而3条曲线在轴向方向上的距离较大，也就是随孔径h的不同，子午球差变化比较大，这正是视场小、相对孔径较大的原因。3条曲线近似为直线，只是斜率不同，说明当视场不太大时，子午彗差与视场成一次方的关系。

（6）子午垂轴像差曲线。

前面曾经指出垂轴像差可以全面地反映系统的成像质量。我们把子午垂轴像差按不同视场、不同孔径做成曲线，即为光学设计中常用的子午垂轴像差曲线。如图1−31所示，从上到下按归化视场1.0ω，0.85ω，0.707 1ω，0.5ω，0.3ω和0ω画出了6条曲线。每条曲线中，横坐标表示孔径h，取相对口径±1.0h，±0.85h，±0.707 1h，±0.5h，±0.3h和0h；纵坐标表示子午垂轴像差δy′。如果计算了其他2种色光的像差，则有3条曲线，分别代表3种颜色光线D，F和C的δy′。

子午垂轴像差曲线在纵坐标上对应的区间表示了子午光束在理想像平面上的最大弥散范围，显然弥散范围越小越好。没有像差的理想曲线应该是一条与横坐标重合的直线。但是，只看最大弥散范围还不足以全面反映系统的成像质量，还要看光能是否集中。如图1−32所示，两个图形曲线的最大弥散范围是一样的，但图1−32（b）中光能均匀分布在像面上，而图1−32（a）中绝大多数光能都集中在一起，只有少量光线离散较大。所以，虽然两个图形的最大弥散范围一样，但后者却比前者成像质量好，甚至即使后者的最大弥散范围再大些，成像质量仍比前者好。

从图1−31中不同视场对应的像差曲线可看出子午垂轴像差随视场变化的规律。不同颜色曲线与纵坐标交点位置之差，表示垂轴色差的大小。当h=0时的光线代表主光线，不同色光主光线在理想像平面上的交点高度之差即为垂轴色差

图1−31　子午垂轴像差曲线

单项几何像差和垂轴像差都能表示系统的成像质量。子午光束具有3种几何像差：。子午垂轴像差曲线和这3种子午像差都表示子午光束的成像质量，只不过各自的表现形式不同，因此它们之间必然有一定的联系。也就是说，子午垂轴像差曲线的形状是由子午像差决定的。由子午垂轴像差曲线可以确定出的大小，反过来也可以由大致想象出垂轴像差曲线的形状。它们之间存在以下关系（图1−33）。

图1−32　垂轴像差弥散范围

（a）光能较为集中；（b）光能较为分散

图1−33　子午垂轴像差与几何像差的关系

图1−34　弧矢垂轴像差曲线

如图1−33所示，将子午光线对a，b连成一条直线，该直线的斜率与宽光束子午场曲成比例。当孔径改变时，连线的斜率也变化，表示随孔径变化的规律。当h→0时，连线斜率便成了过原点的切线斜率，这时，所以在原点处的切线斜率正比于细光束子午场曲我们知道子午球差，所以子午光线对连线与过原点处切线的夹角正比于宽光束子午球差。显然夹角越大，子午球差越大。某子午光线对连线和纵坐标的交点到原点的距离，就是该孔径对应的子午彗差，交点高度越高，越大。

（7）弧矢垂轴像差曲线。

同样，弧矢垂轴像差可以全面地反映弧矢光束在理想像平面上的弥散情况。如图1−34所示，横坐标代表孔径，纵坐标代表δy′，δ z′，共做出了5个视场（1.0ω，0.85ω，0.707 1ω，0.5ω，0.3ω）的曲线。前面说过，由于弧矢光束对子午面对称，只需计算前半部+h。但为了清楚起见还是把后半部−h也画上。前后两半部的弧矢光线对的δy′，δz′有如下关系：

与子午垂轴像差曲线类似，弧矢垂轴像差曲线和弧矢宽光束几何像差的关系，与子午垂轴像差曲线和子午宽光束几何像差的关系是一样的。

上面讨论的像差曲线是经常用到的。在实际设计中，并不是所有的曲线都要画出，系统的光学特性要求不同，需要画出的曲线也不同，应根据情况灵活掌握。