垂轴像差及计算方法

第1.5节所介绍的几何像差的特点是用一些独立的几何参数来表示像点的成像质量，即用单项独立几何像差来表示出射光线的空间复杂结构。用这种方式来表示像差的特点是便于了解光束的结构，分析它们和光学系统结构参数之间的关系，以便进一步校正像差。但是应用这种方法的缺点是几何像差的数据繁多，很难从整体上获得系统综合成像质量的概念。这时我们用像面上子午光束和弧矢光束的弥散范围来评价系统的成像质量更加方便，它直接用不同孔径子午、弧矢光线在理想像平面上的交点和主光线在理想像平面上的交点之间的距离来表示，称为垂轴几何像差。由于它直接给出了光束在像平面上的弥散情况，反映了像点的大小，所以更加直观、全面地显示了系统的成像质量。

如图1−23所示，为了表示子午光束的成像质量，我们在整个子午光束截面内取若干对光线，一般取±1.0h，±0.85h，±0.707 1h，±0.5h，±0.3h，0h这11条不同孔径的光线，计算出它们和理想像平面交点的坐标，由于子午光线永远位于子午面内，因此在理想像平面上交点高度之差就是这些交点之间的距离。求出前10条光线和主光线（0孔径光线）高度之差即为子午光束的垂轴像差：

图1−23　子午垂轴像差(www.xing528.com)

对称于子午面的弧矢光线通过光学系统时永远与子午面对称，如图1−24所示。只需要计算子午面前或子午面后一侧的弧矢光线，另一侧的弧矢光线就很容易根据对称关系确定。弧矢光线BD+经系统后与理想像平面的交点不再位于子午面上，因此相对主光线和理想像平面交点的位置用二个垂直分量δy′和δz′表示，δy′和δz′即为弧矢光线的垂轴像差。和BD+成对的弧矢光线BD−与理想像平面的交点的坐标为（δy′，−δz′），所以只要计算出了BD+的垂轴像差，BD−的垂轴像差也就知道了。

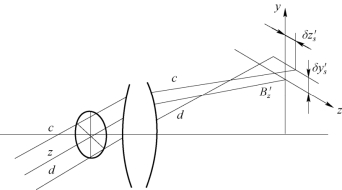
图1−24　弧矢垂轴像差

为了用垂轴像差表示色差，可以将不同颜色光线的垂轴像差用同一基准像面和同一基准主光线作为基准点计算各色光线的垂轴像差。与前面计算垂轴色差时一样，我们一般采用平均波长光线的理想像平面和主光线作为基准计算各色光光线的垂轴色差。为了了解整个像面的成像质量，同样需要计算轴上点和若干不同像高轴外点的垂轴像差。对轴上点来说，子午和弧矢垂轴像差是完全一样的，因此弧矢垂轴像差没有必要计算0视场的垂轴像差。

在计算垂轴像差δy′时以主光线为计算基准，这样做的好处是把畸变和其他像差分离开来。畸变只影响像的变形，而不影响像的清晰度。垂轴像差δy′以主光线为计算基准，它表示光线在主光线周围的弥散范围，δy′越小，光线越集中，成像越清晰，所以δy′表示成像的清晰度。而如果以理想像点作为计算基准，就把畸变和清晰度混淆在一起了，不利于分析和校正像差。