如何正确处理轴外像点的单色像差

对于轴外点来说，情况就比轴上点要复杂得多。对于轴上点，光轴就是整个光束的对称轴线，通过光轴的任意截面内光束的结构都是相同的，因此只需考察一个截面即可。而由轴外物点进入共轴系统成像的光束，经过系统以后不再像轴上点的光束那样具有一条对称轴线，只存在一个对称平面，这个对称平面就是由物点和光轴构成的平面，如图1−20中的ABO平面。轴外物点发出的通过系统的所有光线在像空间的聚交情况就要比轴上点复杂得多。为了能够简化问题，同时能够定量地描述这些光线的弥散程度，我们从整个入射光束中取两个互相垂直的平面光束，用这两个平面光束的结构来近似地代表整个光束的结构。这两个平面，一个是光束的对称面BM+M−，称为子午面；另一个是过主光线BP与BM+M−垂直的BD+D−平面，称为弧矢面，用来描述这两个平面光束结构的几何参数分别称为子午像差和弧矢像差。

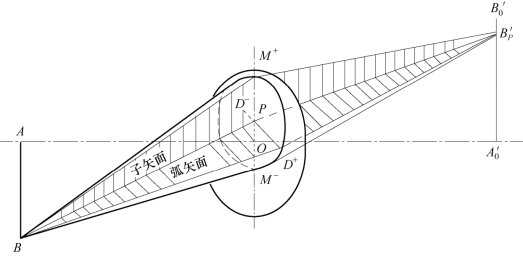
图1−20　子午面与弧矢面示意图

（1）子午像差。

由于子午面既是光束的对称面，又是系统的对称面，该平面内的子午光束通过系统后永远位于同一平面内，因此计算子午面内光线的光路是一个平面的三角几何问题。可以在一个平面图形内表示出光束的结构，如图1−21所示。

图1−21　子午面光线像差

图1−21为轴外无限远物点发来的斜光束的光路图。与轴上点的情形一样，为了表示子午光束的结构，我们取出主光线两侧具有相同孔径高的两条成对的光线BM+和BM−，称为子午光线对。该子午光线对通过系统以后当然也位于子午面内，如果光学系统没有像差，则所有光线对都应交在理想像平面上的同一点。由于有像差存在，BM+和BM−光线对的交点既不在主光线上，也不在理想像平面上。为了表示这种差异，我们用子午光线对的交点离理想像平面的轴向距离表示此光线对交点与理想像平面的偏离程度，称为“子午场曲”。用光线对交点离主光线的垂直距离表示此光线对交点偏离主光线的程度，称为“子午彗差”。当光线对对称地逐渐向主光线靠近，宽度趋于零时，它们的交点趋近于一点点显然应该位于主光线上，它离开理想像平面的距离称为“细光束子午场曲”，用表示。不同宽度子午光线对的子午场曲和细光束子午场曲之差代表了细光束和宽光束交点前后位置的差。此差值和轴上点的球差具有类似的意义，因此也称为“轴外子午球差”，用表示：

它描述了光束宽度改变时交点前后位置的变化情况。和这3个量即可表示子午光线对BM+和BM−的聚交情况。为了全面了解整个子午光束的结构，一般取出不同孔径高的若干个子午光线对，每一个子午光线对都有自己相应的和值。孔径高的选取和轴上点相似，取（±1，±0.85，±0.707 1，±0.5，±0.3）hm，其中hm为最大孔径高。同时，为了了解整个像平面的成像质量，还需要知道不同像高轴外点的像差，一般取1，0.85，0.707 1，0.5，0.3这5个视场来分别计算出不同孔径高子午像差和的值。

（2）弧矢像差。

弧矢像差可以和子午像差类似定义，只不过是在弧矢面内。如图1−22所示，阴影部分所在平面即为弧矢面。处在主光线两侧与主光线距离相等的弧矢光线对BD+和BD−相对于子午面显然是对称的，它们的交点必然位于子午面内。与子午光线对的情形相对应，我们把弧矢光线对的交点到理想像平面的距离用表示，称为“弧矢场曲”；到主光线的距离用表示，称为“弧矢彗差”。主光线附近的弧矢细光束的交点到理想像平面的距离用表示，称为“细光束弧矢场曲”；称为“轴外弧矢球差”，用表示。

(www.xing528.com)

由于弧矢像差和子午像差比较，变化比较缓慢，所以一般比子午光束少取一些弧矢光线对。另外，与子午光线一样，为了了解整个像平面的成像质量，还需要知道不同像高轴外点的像差，一般取1.0，0.85，0.707 1，0.5，0.3这5个视场来分别计算出不同孔径高的弧矢像差和的值。

图1−22　弧矢面光线像差

对于某些小视场大孔径的光学系统来说，由于像高本身较小，彗差的实际数值更小，因此用彗差的绝对数量不足以说明系统的彗差特性。一般改用彗差与像高的比值来代替系统的彗差，用符号SC′表示：

SC′的计算公式为

对于用小孔径光束成像的光学系统，它的子午和弧矢宽光束像差和不起显著作用。它在理想像平面上的成像质量由细光束子午和弧矢场曲决定。之差反映了主光线周围的细光束偏离同心光束的程度，我们把它称为“像散”，用符号表示：

像散等于零说明该细光束为一同心光束；否则为像散光束。但是不一定为零，也就是光束的聚交点与理想像点不重合，因此仍不能认为成像符号理想。

对于一个理想的光学系统来说，不仅要求成像清晰，而且要求物像要相似。上面介绍的轴外子午和弧矢像差，只能用来表示轴外光束的结构或轴外像点的成像清晰度。实际光学系统所成的像即使上面所说的子午像差和弧矢像差都等于零，但对应的像高并不一定和理想像高一致。从整个像面来看，物和像的几何形状就不相似。我们把成像光束的主光线和理想像平面交点的高度作为光束的实际像高。和理想像高之差为，如图1−22所示：

用它作为衡量成像变形的指标，称为畸变。