星点检验：检测阶段的像质评价指标

任何一个实际的光学系统都不可能理想成像，即成像不可能绝对的清晰和没有变形，所谓像差就是光学系统所成的实际像与理想像之间的差异。由于一个光学系统不可能理想成像，因此就存在一个光学系统成像质量优劣的评价问题。成像质量评价的方法分为两大类：第一类用于在光学系统实际制造完成以后对其进行实际测量；第二类用于在光学系统还没有制造出来，即在设计阶段通过计算就能评定系统的质量。对于第一类像质评价方法，主要有“分辨率检验”和“星点检验”。由近代物理光学知道，利用满足线性与空间不变性条件的系统的线性叠加特性，可以将任何物方图样分解为许多基元图样，这些基元对应的像方图样是容易知道的，然后由这些基元的像方图样线性叠加得出总的像方图样。从这一理论出发，当光学系统对非相干照明物体或自发光物体成像时，可以把任意的物分布看成无数个具有不同强度的、独立的发光点的集合，我们称点状物为物方图样的基元即点基元。这里，也可以理解为一个无限小的点光源物，如小星点，故可采用单位脉冲δ函数作为点基元，有如下数学关系：

因系统具有线性和空间不变性，有如下物像关系式：

式中，（，）Ouv为物方图样；（，）iuv′′为像方图样；u，v和u′，v′分别对应物面和像面的笛卡儿坐标；Mu，Mv为物像的横向放大率；h（u′−Muu，v′−Mvv）为系统的点基元像分布，即（，）uv处的一个点基元物（，）uvδ的像。

式（1−3）表示了线性空间不变系统的一个成像过程，即将任意物强度分布与该系统的点像分布卷积就得到像强度分布，点物基元像分布完全决定了系统的成像特性。只有当点物基元像分布仍为δ函数时，物像之间才严格保证点对应点的关系。

实际上每一个发光点物基元通过光学系统后，由于衍射和像差以及其他工艺疵病的影响，绝对的点对应点的成像关系是不存在的，卷积的结果是对原物强度分布起了平滑作用，从而造成点物基元经系统成像后的失真，因此采用点物基元描述成像的过程，其实质是一个卷积成像过程，通过考察光学系统对一个点物基元的成像质量就可以了解和评定光学系统对任意物分布的成像质量，这就是星点检验的基本思想。

对一个无像差衍射受限系统来说，其光瞳函数是一个实函数，而且在光瞳范围内是一个常数。因此，衍射像的光强分布仅仅取决于光瞳的形状。在一般圆形光瞳的情况下，衍射受限系统星点像的光强分布函数就是圆孔函数傅里叶变换的模的平方，即艾里斑光强分布式为

式中，φ=（2π/λ）hθ=（πD/λf′）r。

式（1−4）所代表的几何图形及各个量的物理意义如图1−7所示。图1−8给出了艾里斑的三维光强分布图及其局部放大图。表1−3给出了艾里斑各极值点的数据。至于焦面附近前后不同截面上的光强分布，也可通过类似的计算求出。

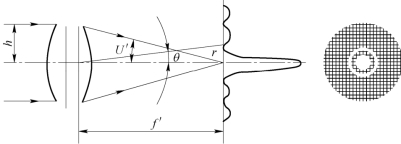
图1−7　夫朗和斐圆孔衍射图

图1−8　艾里斑的三维光强分布图及其局部放大局（在相对强度0.03处截断）

表1−3　艾里斑各极值点数据

图1−10所示为焦点前后不同截面上的星点图。由图1−9和图1−10可以看出，一个具有圆形光瞳的衍射受限系统，不仅在焦面内应具有图1−7和图1−8所示的艾里斑分布规律，而且在焦点前后应具有对称的光强分布。(www.xing528.com)

图1−9　子午面内的等强度线

图1−10　焦点前后不同截面上的星点图

显然，当光学系统的光瞳形状改变时，其理想星点像也应随之改变。例如，折反射光学系统的光瞳通常是圆环形的，其焦面上理想像的光强分布式为

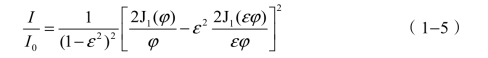
式中，ε为环形孔内外两个同心圆的半径之比。图1−11为具有不同开孔比ε时焦平面内的光强分布曲线；图1−12为其三维光强分布图。在光学仪器中偶尔也会遇到方形或矩形光瞳的情况，如图1−13所示。这时焦平面内的理想星点像光强分布式为

图1−11　环形孔理想星点像的光强分布曲线

（a）ε=0；（b）ε=0.5；（c）ε→1

式中，a，b分别为矩形光瞳长宽方向的宽度。

根据星点像判断光学系统的像质好坏，尤其是进一步“诊断”光学系统存在的主要像差性质和疵病种类，以及造成这些缺陷的原因，这在光学仪器生产实践中具有重要意义。但要对星点检验结果做出准确可靠的分析、判断，不仅要掌握星点检验的基本原理，还要有丰富的实践经验，所以有关星点像的分析和像差判断必须在实践中不断地总结和积累。

图1−12　环形孔理想星点像的三维光强分布图

（a）ε=0；（b）ε=0.5；（c）ε=0.8

图1−13　方形光瞳理想星点像的三维光强分布图