火力分配模型的求解的分析介绍

多目标分配的常规做法是以整体优势最大或者以整体威胁最小的方式进行分配，每次都只给出一个分配结果且都是取极端值，这难以满足决策者的偏好和实际作战中面临各种不同情况的需要。基于进化多目标分配优化算法，可一次找出多个优化的分配结果的一个解集，并且使这些解集中的解尽可能逼近Pareto 前沿解。

将改进的遗传算法用于多目标优化，即最优保存的非劣分层遗传算法（NSGA-Ⅱ）。NSGA- Ⅱ属于Pareto 排序与竞争法的一种。在NSGA- Ⅱ中，首先用亲代种群Pn 只建立子代种群Qn ，并将两个种群联合在一起形成大小为2N 的种群Rn 。然后使用非劣分层将整个种群Rn 分层。尽管与只对Qn 进行非劣分层相比，它需要做更多的工作，但是它允许在整个子代和亲代进行全局的非劣检验。一旦结束非劣分层，新种群Pn+1 由不同的非劣层的个体填充，每次一层。填充过程从最优非劣层开始，接着是第二非劣层，再接着是第三非劣层，等等。由于整个种群Rn 的种群大小为2N，新种群的N 个位置不能容纳所有的非劣组，删除所有不能被容纳的非劣组。当考虑被允许的最后一组非劣层时，该非劣层可能存在比新种群剩下位置更多的个体。在这种情况下，使用小生境策略从最后一组选择位于该组较稀疏区域的个体填充满该种群。这里着重要指出的是，Rn 的非劣分层过程和种群Pn+1 的填充过程可以一起执行。这样，每次找到一个非劣层并检查它的大小，看它是否能被新种群容纳，如果不能，那么就不必再进行非劣分层，这样能减少该算法的运行时间。其主要步骤如下：

（1）初始种群建立。

（2）Pareto 集非劣分层。

（3）遗传进化操作（交叉、变异、选择）。

（4）父代和子代合并。

（5）新种群筛选。

（6）最优非劣Pareto 解集。

首先，建立一个随机初始种群P0 并初始化进化代数计数器n = 0 。然后对种群的所有个体进行非劣分层，并计算每一非劣层所有个体的拥挤距离。接着使用二规模联赛选择算子（后面将要介绍拥挤联赛选择算子）、交叉算子和变异算子建立规模为N 的子代种群Qn 。最后，对联合的亲代种群和子代种群进行非劣分层并填充新一代种群Pn+1 。进化代数计数器n 加1 并判断n 是否大于最大进化代数MaxGen。如果是，那么该算法结束；否则，继续进化。如此循环，直到进化到指定的最大进化代数。该算法中对联合的亲代种群和子代种群进行非劣分层并填充新一代种群Pn+1 的过程：对Rn 辨识非劣组并判断该非劣组能否被新种群容纳。如果能，将该非劣组的所有个体填充到新种群并将它们从Rn 中删除，继续辨识非劣组并判断该非劣组能否被新种群容纳。如此反复，直到不能容纳该非劣组的所有个体。对最后不能被完全容纳的非劣组中的个体计算拥挤距离并选择分布最广的个个体填充新种群。

以上的小生境策略在进化的早期阶段不会太大地影响此算法的进程。这是因为在早期阶段联合种群有许多非劣组，可能新的种群在它被填满之前已经包括了许多好的非劣组的个体，它几乎不用处理该选择哪个个体填充种群。然而，在仿真的后期阶段，可能种群的大多数个体来源于最优非劣组，也可能在种群大小为2N 的联合种群Rt 中，最优非劣组的个体数超过了N，那么以上的算法确保了小生境策略将从这一组个体中选择互异性大的个体。当整个种群收敛到Pareto 最优域时，该算法的继续执行可确保得到一组分布更好的个体。

进化类方法Pareto 集中最优个体是根据个体在种群中相对于其他个体的优劣来确定的。图5-2所示为两个目标函数的Pareto 集非劣分层示意图，根据每个个体在多目标函数值空间中的位置来确定其优劣性，然后进行统计可以得到其所处的分层结构，图中给出了三个分层曲线，第一层由绿色曲线对应的5个个体组成，称为Pareto 前端，即第一非劣层，可以看到如个体A，其所对应的占优区内个体数目均为0，其个体对应的秩为1；第二层由红色曲线对应的5 个个体组成，称为第二非劣层，如个体B，其所对应的占优区包含的个体数目均为1，其个体对应的秩为2；第三层为蓝色曲线对应的3 个个体，称为第三非劣层，如个体C，其所对应的占优区个体数目为2，其个体对应的秩为3。Pareto 集非劣分层就是将解空间中的所有个体进行类似有效的非劣分层，以区分其优劣关系，进而为选择具有优势的解集合提供依据。图5-3 给出了基于子空间统计的Pareto 集非劣分层方法流程。

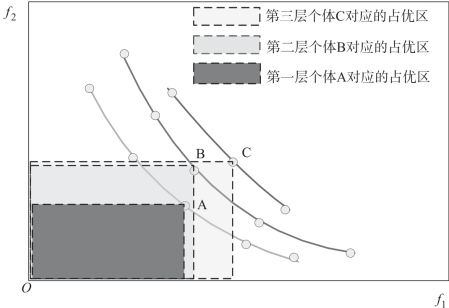
图5-2　Pareto 集非劣分层示意

图5-3　拥挤联赛选择算子流程

现有的进化类算法Pareto 集非劣分层需要遍历种群中所有个体而耗时太大导致算法实时性不强的缺点，提供了一种多目标优化Pareto 集非劣分层方法，该方法通过对多维空间的子空间划分来进行多目标优化的Pareto 集快速非劣分层，提高优化算法的效率。

NSGA-Ⅱ对整个亲代和子代种群执行非劣分层，然后再进行种群筛选，选出初始种群规模大小的种群，具体筛选策略是：从最优非劣解开始，接收每层的个体直到填满所有的种群位置，因此该算法也为最优保存型。对于允许填充的最后一层的个体，使用基于拥挤距离的小生境策略进行选择。该项研究也介绍了拥挤距离尺度，该尺度使得算法既快又能变换到处理两个以上的目标。

在多平台火力分配中，其目标函数为双目标约束优化问题，即作战效能最大和武器用量最小。WTA 的三个基本原则构成约束条件——对每个来袭的敌方目标均要分配导弹进行拦截；每种型号的武器分配的数目不能超过该武器的资源数目；每种武器可对同一敌方来袭目标分配多枚导弹。(www.xing528.com)

1.约束条件处理方式

以违约淘汰法和罚函数法处理约束条件。违约淘汰法是每产生一个个体后即进行约束条件判断，如果不满足约束条件，则直接抛弃该新生个体，父本个体进入下一代；罚函数法是一种较普通的约束处理策略，通过将约束条件加权为惩罚值并入到第一个目标函数中变成无约束优化问题。

2.编码方式

编码是将问题的解用基因码字表示的过程，是解从表现型到基因型的转变。常用的编码方式有二进制编码、实数编码、整数或字母排列编码和一般数据结构编码等。对于多平台协同火力分配问题，由于每个平台武器的弹药数量为整数，因此，用二进制编码不太适合，拟采用十进制整数编码。火力分配问题具体编码规则如下：

（1）按目标顺序排列分配每种武器给每个目标的弹药数目。

（2）将每个目标分配的导弹码字串在一起，形成总的染色体。

具体编码实施方法是：假定有m 个敌方目标，多平台武器有n 组武器。采用十进制编码，每个染色体由按目标顺序排列的武器编号组成，表示一种可能的分配方案，其中每个基因表示一批目标的分配结果，染色体的长度为m × n。编码基因的取值范围在每种武器拥有的导弹数目总量以内，不同的基因可取相同的编码值。m 取4，n 取3，则种群的1 个染色体216973480531 表示一个火力分配方案，即第1 种武器分配给4 个目标的导弹数目分别是2、1、6、9，第2 种武器分配给4 个目标的导弹数目分别是7、3、4、8，第3 种武器分配给4个目标的导弹数目分别是0、5、3、1。

采用十进制编码的好处是简单直观，不需要复杂的解码函数，但是这样编码在交叉或者变异运算中会出现染色体基因重复的现象，为了避免这种情况的发生，常常采取的挽救措施是当出现了染色体重复的基因，把经过交叉或者变异后重复的基因删除，然后用没有出现的基因代替，代替以后所生成的新的染色体并不是最终的染色体，还要继续对它进行进化运算，最终得到符合要求的染色体。

3.初始化种群

对于进化类优化算法来说，初始种群的个体特性对后期算法寻优效果将产生重要影响，普通随机初始化得到的种群易于过早收敛于局部极值。而具有良好多样性的初始种群，其个体分布均匀，彼此离散度高，有助于提高算法的收敛速度和求解精度，降低算法陷入局部极值的概率，有效地缓解算法早熟现象。

本课题采取的办法是开始时先生成一个比所需群体规模要大很多的初始群体，从该群体中再随机选取适应值达到要求的个体。为了保障算法的实时性，如果选择次数超过某一规定的数值或者选择的时间超过了给定值就不再进行选择，直接利用初始化得到的群体开始进行遗传操作。这种方法经过编程实验，效果显著，对于提高全局解的最优性和加快算法的收敛速度起着很大的作用。

应遗传算法的操作要求，需为遗传操作准备若干个解个体组成的初始群体。初始群体的生成涉及两个内容：其一是群体的规模，其二是群体的生成方式。目前尚无定则来设计初始群体的规模大小，本书的处理方法是，先对不同的群体规模，如30、50、80、100、200 等进行分别训练，再从中选用合适的规模大小。群体的生成一般采用随机生成的办法，采用预处理先验知识来生成部分初始群体，以提高算法的收敛速度。其具体办法是：在预处理中对每个目标的威胁等级和战术价值进行排序，先取威胁等级排名前的目标位攻击。

4.遗传操作

遗传操作是进化类算法的核心思想所在，即根据生物进化特征对种群进行进化的过程，对于遗传算法，其遗传操作主要包括选择算子、交叉算子和变异算子三种典型操作。选择算子采用轮盘赌方法，其特点是它为一个随机采样过程，操作简单，实用性强。交叉算子仿生生物学中的基因重组，即染色体通过交换基因实现杂交。交换染色体的基因是遗传算法的本质操作，正是通过染色体基因的交换、重组，得到新的染色体，才使得实际问题的解不断向着优化的方向发展。变异算子是模拟生物进化的基因变异过程，实现基因的多样化，它以一定概率Pm 选出父代个体以进行变异操作，改变基因串中指定位置的码元。

5.进化算法参数选择

进化参数的选择包括：种群规模、交叉概率、变异概率和算法终止条件等，在前面的步骤中对于种群规模、交叉概率和变异概率均有所介绍。遗传算法需设计终止规则以停止系统的演化。终止规则可采用最大演化系数（遗传代数）或某适应度闭值。本书采用试探的办法来确定系统终止规则。采取了遗传的最大代数为算法的终止条件，如果满足条件，算法即结束。

遗传算法的最终目的就是寻找最优的解，传统的算法是进行了一次遗传操作后对个体进行评价，找到最优解，但是这样做很有可能错过最优解，原因是最优解并不一定出现在一次迭代的结束，在算法中间很可能出现，如在交叉、变异后均可能出现最优解，因此在每次交叉、变异后均寻找当前的最优解，并把该解与上次得到的最优解进行比较，选择累积的最优解，这样可以在一旦发现最优解时立刻终止算法，不会造成时间的浪费。