威胁评估算法优化：解析威胁级别

在将目标的威胁因素指标确定并计算出隶属度之后，需要对目标威胁进行排序，本节针对目标威胁排序算法进行研究，主要介绍几种常用的算法，并结合装甲车辆的实际情况，选取一种算法开展研究。

1.基于专家系统的目标威胁评估算法

专家系统一般是指拥有某领域特定的知识和经验的计算机辅助决策支持系统。为了对这些知识和经验进行存储，还必须对它们进行一定的加工，将它们翻译成计算机能够读懂的语言存放在系统内。因此，一个拥有某领域大量专家知识的专家系统就可以模仿人类专家的行为，对这个领域的相关问题进行分析和求解。

专家系统的理论基础以认知科学为主，并广泛吸收诸多领域的相关研究成果。认知科学的主要任务就是研究人类如何根据从外界得到的各种信息来解决问题，而以认知科学为基础发展而来的专家系统就是力图通过计算机系统来模拟人类解决问题的过程。但是在有关研究中发现，即使是有经验的专家，有时也不能完全解释自己是如何解决问题的。研究发现，一个基于精确知识集、没有学习能力的专家系统，对于不能解释自己是如何解决问题的情形，将无法完成工作。因此，一个好的专家系统，除了需要建立一个精确的知识库以外，更重要的是还要有一定的自我学习能力，通过知识的学习更新，提高其模拟人类专家解决问题的能力。

基于专家系统的威胁判断系统的结构如图4-9所示。

系统首先接收来自探测设备的情报信息，经数据融合等算法预处理后，得到目标的综合信息。在进行威胁判断之前，还需要根据当前目标的位置等信息综合判断企图。如果发现目标有企图，则进行拦截适宜性检查，对可拦截目标进行威胁估计并分配给适宜的武器系统。系统的知识库中存有目标的可拦截条件和威胁等级判断的准则。其中，判断准则的制定综合考虑了作战特点、态势、敌我双方的兵器性能等因素，能够使威胁估计的结果更贴近目标的实际情况。推理机首先根据目标类型调用该类目标的威胁判断模型，然后综合利用知识库里的知识，综合数据库的数据和实时情报在推理机中完成推理工作。为了使系统满足实时性和动态性的特点及要求，推理机将在基本知识的控制下采用一种名为“触发式”的双向混合推理模式。人机接口不仅可以为指挥员提供推理原则和推理过程，还可以为指挥员提供人工干预的通道。根据实际战场形势的不同，指挥员还可以通过人机接口修改、增减系统的知识库，使其能够更好地适应当前的战场态势。

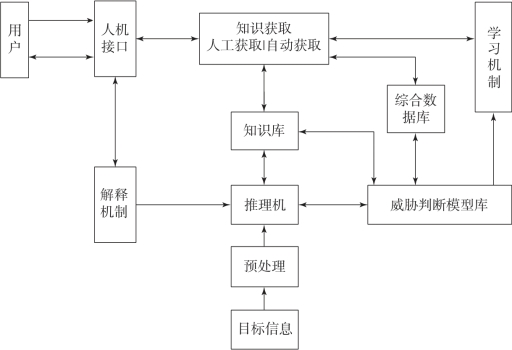
图4-9　基于专家系统的威胁判断系统的结构

2.基于贝叶斯推理的目标威胁评估算法

贝叶斯网络（Bayesian networks，BN）是基于图形模式的变量间概率分布的表示方法，其数学基础稳固，语义形象直观，被广泛应用于不确定性知识表示和推理等。贝叶斯网络作为人工智能领域中的一个重要研究课题，综合考虑了先验信息和样本数据，充分利用了专家知识和先验经验知识，可以综合地进行定量分析和定性分析。经过30 多年的发展，目前贝叶斯网络已经成为人工智能和专家系统中的一个研究热点。与其他知识表示形式如规则库、决策树、人工神经网络等相比，贝叶斯网络具有图形化的模型表示形式、局部及分布式的学习机制、直观的推理，适用于表达和分析不确定性与概率性的事物等优点，是人工智能的大部分领域，包括因果推理、不确定性知识表达、模式识别和分类、聚类分析等应用的有效工具。

图4-10所示为一个典型的贝叶斯网络，贝叶斯网络主要由有向无环图（directed acyclic graph，DAG）和条件概率表（conditional probability table，CPT）两部分构成。有向无环图通常称为贝叶斯网络结构，其网络结构是一个具有n 个节点的有向无环图，每个节点代表离散的随机变量，可以是各种待求解的推理问题的抽象；连接节点的有向边代表了节点之间的因果关系，弧的指向代表因果影响的方向性（由父节点指向子节点）。条件概率表反映了变量之间关联性的局部概率分布情况，它表达了子节点同其父节点的相关关系。没有任何父节点的条件概率为其先验概率。有了节点及其相互关系（有向边）、条件概率表，贝叶斯网络就可以表达网络中所有节点的联合概率，并可以根据先验概率信息或某些节点的取值（获取的证据）计算其他任意节点的概率信息，即进行网络推理。

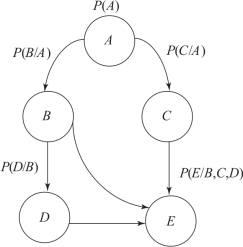
图4-10　典型的贝叶斯网络

本课题采用贝叶斯网络建立目标威胁等级评估模型，该方法可以很好地解决威胁估计的关键问题，结合专家知识和基于不确定信息的推理，将其应用于威胁评估，具备以下优势。

（1）贝叶斯网络使用图形化的模型对陆战场领域知识进行表达，同时通过具有语义性的推理逻辑对不确定性问题进行求解，符合人类的思维模式。

（2）贝叶斯网络将领域知识和专家经验（先验信息）与战场观测到的事件（样本数据）有机结合起来，不仅避免了主观因素可能造成的偏见，而且削弱了样本数据带来的噪声问题。

（3）贝叶斯网络实现了定性分析与定量分析的有机结合。它能够在战场数据不完备的情况下从战场事件推断目标的威胁等级，其基于概率模型和概率语言的推理方式保证了推理结果具有很高的可信性。

（4）贝叶斯概率的特点使网络模型能够反映威胁估计的连续性和累积性这两个重要特征。

依据前节确定的威胁意图要素，构建贝叶斯网络，并通过贝叶斯推理得到每个目标对各个平台的威胁意图状态概率，概率值最大的状态即该目标的威胁意图。

构建目标威胁估计的贝叶斯网络模型，需要经过以下三个步骤。

（1）确定节点及节点状态。对于装甲车辆的目标威胁估计来说，节点代表的就是装甲车辆协同作战中可能发生的事件。在现实中，事件的发生常常具有多种情况，相应地，网络中的节点也可以有多个状态，这些状态之间彼此独立，每个都代表了一种假设。举例来说，如果将“敌方目标威胁等级”作为威胁估计的顶层事件，那么它对应的节点就可能包含“威胁等级高”“威胁等级低”等多个状态。

（2）确定节点关系。在确定了节点事件之后，接下来需要明确的是各个节点事件之间的因果关系，这些关系用有向弧表示。例如，当敌方坦克意图对我进行榴弹攻击（记为事件X ）时，通常会先进行减速（记为事件Y ），基于这种影响关系，如果将前者作为“原因”，那后者就是“结果”，两者之间的关系可以用有向弧X→Y 表示。

（3）节点概率分配。概率分配包括两部分内容：对没有父节点的顶层事件指定先验概率，对有父节点的事件指定条件概率。节点概率通常是在网络初始化时由作战专家根据经验指定的。

在利用贝叶斯网络进行问题求解时，那些值已确定的变量构成的集合称为证据D，需要求解的变量集合称为假设X ，基于贝叶斯网络的目标威胁估计就是求解给定证据（已发生的战场事件）的条件下假设变量（目标威胁等级）的后验概率P（X/D）。(www.xing528.com)

贝叶斯网络在构造威胁评估分析模型方面也有许多优点。

（1）将因果知识用有向图直观地表示出来，同时又将条件概率加入模型中，使先验知识和后验数据完美结合。

（2）图形化地表示了各随机变量间的联合概率分布，可以有效地处理各种不确定性信息。

（3）模型可以反映出目标威胁分析的累积性和连续性，分析结果在反映当前信息的同时还结合了先验知识。

由贝叶斯网络的定义可知，构建一个与研究突击作战领域相关的贝叶斯模型包括以下几个方面。

（1）确定需要用哪些相关变量来描述该领域和每个变量的可能值。

（2）确定各变量间的依赖关系，并构建其网络结构。

（3）量化变量之间的依赖关系，确定条件概率分布。

（4）在实际系统中运用，通过数据优化贝叶斯网络。

对于装甲车辆协同作战的目标威胁分析评估的贝叶斯网络模型如图4-11所示。

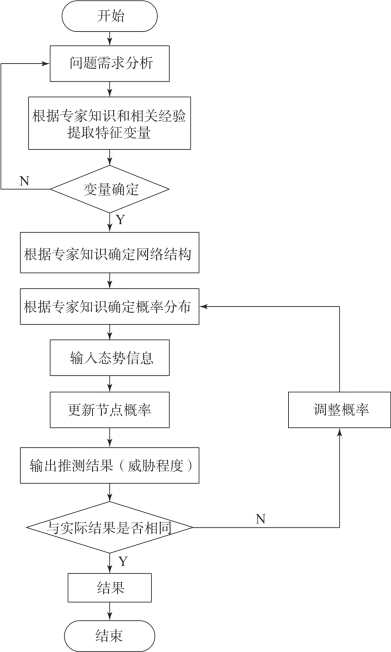
图4-11　目标威胁分析评估的贝叶斯网络模型

贝叶斯网络中，当某个节点获取证据信息后，该信息就在网络中进行传播，最终每个节点的概率都得到了更新。此外，由贝叶斯网络的条件独立性、概率可推理性以及知识的定量表示特性等特点可以看出，贝叶斯网络能很好地满足态势估计系统的推理要求。

图4-12所示的威胁评估贝叶斯网络结构中，由传感器系统对目标实体信息进行探测及融合处理后，通过融合系统获取融合后的实时证据信息和训练数据。将证据信息模糊处理后，直接作为证据更新网络的节点概率，同时训练数据用来进行周期性网络参数学习。目标威胁分析系统将融合系统的传入数据及环境中其他形式的证据信息作为证据输入，通过贝叶斯网络推理后，最终输出对当前目标威胁的预测。

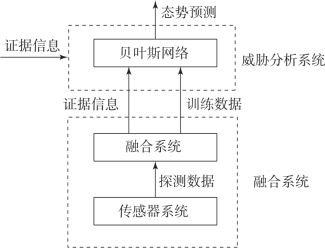
图4-12　威胁评估贝叶斯网络结构

3.基于灰色关联度分析的目标威胁评估算法

灰色关联分析是一种多因素统计分析方法。它以各因素的样本数据为依据，用灰色关联度来描述因素间相关性的强弱。其基本思想是根据序列曲线几何形状的相似程度来判断其联系是否紧密。曲线越接近，相应序列之间关联度就越大；反之，关联度就越小。灰色关联度分析法的目的就是寻求一种能衡量各因素间关联程度的量化方法，该方法弥补了采用数量统计方法做系统分析所导致的缺憾。无论样本量多少和样本有无规律，它都同样适用，而且计算量小，十分方便，更不会出现量化结果与定性分析结果不符的情况。与传统的多因素分析方法相比，灰色关联度分析对数据要求较低，而且考虑了所有给出的信息，不会造成数据的失真。但灰色关联度分析只是对数据本身进行分析，缺少定性的描述，本节在灰色关联度分析方法中加入专家权重，这样定量与定性相结合，使可信度进一步增强。

采用灰色关联度分析方法对一个系统或现象进行分析时，按照定义的算式可得灰色关联度分析的计算步骤：第一步，选取反映系统行为特征的数据序列；第二步，对各序列求取初值项；第三步，求差序列；第四步，求最大差与最小差；第五步，求关联系数；第六步，计算关联度。

本书对灰色关联分析方法进行了改进。

（1）在数据分析序列采用第4 章中的目标威胁因素的隶属度值，由于其已经进行归一化处理，因此可以将第二步求取初值项省略。

（2）在第六步计算关联度时，与二元对比法获得的五个目标威胁因素权重进行联合计算，达到定量与定性相结合的目的。

（3）使用将最优关联度与最劣关联度兼顾的综合关联度来解决威胁排序结果有可能不完全一致的问题。