药物扩散与药用高分子材料的应用

1.药物通过高分子材料的传质过程

在药物制剂中，药物通过高分子材料的扩散可概括为储库型和骨架型两类模型。药物一般是溶解或分散在高分子材料中。药物从高分子材料中扩散的过程可以分为以下几个步骤：①药物溶出并进入周围的高分子材料或空隙；②由于存在浓度梯度，药物分子扩散通过高分子材料屏障；③药物由高分子材料解吸附；④药物扩散进入体液或介质。药物在高分子材料中的扩散性必须具有所需要的渗透速度，因此，理解药物在高分子材料中的扩散以及药物通过高分子材料转运的机制在药物的释放过程中是至关重要的。通常情况下可以根据转运机制确定溶质的扩散类型，而溶质分子大小和高分子材料的结构则制约着溶质的扩散系数，从而控制了溶质的释放速度。在药物制剂中，药物的释放过程很少有对流产生，生要为分子的扩散。

（1）Fick扩散。药物分子通过高分子材料的扩散，可以采用Fick第一定律来描述：

式中J——溶质流量，mol/（cm2·s）；

c——溶质浓度，mol/cm3；

x——垂直于有效扩散面积的位移，cm；

D——溶质扩散系数，cm2/s

在通常情况下，D被看成是常量，但实际上扩散系数是可人为控制的参数，改变高分子材料的结构，D值可改变。另外，药物浓度、温度、溶剂性质、药物的化学性质都能影响D值。负号表示扩散方向，即药物分子扩散朝浓度降低的方向进行。

Fick第一定律给出了稳态扩散的药物流量，在非稳态流动时，可用Fick第二定律来描述。

式（6.1.2）表示在扩散场中的任一固定容积单位中，药物浓度在一固定方向x的改变。

（i）药物通过高分子材料薄膜的扩散。在药剂学的实际应用中，药物通过薄膜的扩散常见的有胶囊壁扩散、高分子材料包衣层扩散。药物与高分子材料之间的亲和力、高分子材料的结晶度对药物的扩散性具有很大的影响。固体高分子材料的晶区是大多数药物分子不可穿透的屏障，因此扩散分子必须绕过它，晶区分子所占的百分比越大，分子的运动越慢。在无孔固体高分子材料中扩散则更为困难，需要移动高分子材料链才能使药物分子通过。对于无孔隙的固体高分子材料薄膜来说，由于高分子材料两侧的浓度差很大，在很长的释放时间内，其差值几乎是常数，假设J和D为常数，在膜厚度为h的范围内积分，可得下式：

式中Δc——薄膜两侧的溶质浓度差，mg/cm3；

K——溶质分配系数；

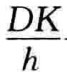——溶质渗透系数（可用P表示），cm/s（常用P来评价药物通过高分子材料的渗透性能）。

由式（6.1.4）可知，D、K值越大，则P值越大，故选择高分子材料时，应注意药物与高分子材料在热力学上的相容性，否则药物是很难通过高分子材料薄膜扩散的。式（6.1.4）的意义很明显，药物通过高分子材料薄膜的释放，应呈零级，因为Δc、D、K和h皆为常数。

（ii）药物通过高分子材料骨架的扩散。对于分散于疏水性骨架中的药物扩散，根据质量平衡原理，Higuchi作了如下的数学处理，其原理如图6.1.1所示。

图6.1.1 药物由骨架扩散的示意图

W—药物总量；

Cs—药物在高分子材料骨架中的饱和溶解度；

h—药物分子扩散路径；B—漏槽

根据图6.1.1，前沿扩散路径移动dh，则扩散的药物量改变d M，则有：

式中W——单位体积高分子材料骨架中总药量，mg/cm3；

M——单位面积扩散出的药物量， mg/cm3；

Cs——药物在高分子材料骨架中的饱和溶解度，mg/cm3；

h——药物分子扩散路径，cm。

根据Fick定律，可得

一般情况下，C0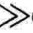Cs，故

式（6.1.7）说明，药物由高分子材料骨架释放量与呈线性关系。

对多孔道的骨架来说（见图6.1.2），Higuchi用下述方程来表达：

图6.1.2 药物由多孔道高分子材料骨架的释放

A—药物；B—高分子材料骨架

式中Ca——药物在释放介质中的溶解度，mg/cm3

Da——药物在释放介质中的扩散系数，cm2/s；

t——任意时间，s；(www.xing528.com)

ε——骨架的孔隙率；

τ——曲折因子；

M——单位面积扩散的药物量，mg/cm2；

C0——药物在骨架内单位体积的药量，mg/cm3

由式（6.1.8）可见，孔隙率越大，释放得越快，曲折因子越大，则分子扩散路径越长，M越小。对于亲水性骨架来说，式（6.1.8）不太适用，因为亲水性骨架中由于水的进入，骨架膨化，药物则由饱和溶液通过凝胶层扩散。有关亲水性骨架的释放，最近的研究引入非Fick扩散的机理。

（2）非Fick扩散。高分子材料的结构特性可能影响药物通过高分子材料的扩散系数，但不会改变扩散机理（Fick扩散）。高分子材料的松弛特性，对溶质通过高分子材料的扩散机制会产生很大影响，如当溶剂（水）穿透一种原本是玻璃态的亲水性高分子材料时，高分子材料-水界面可能出现一个膨胀层，此时大分子链的松弛可影响药物的扩散释放。如将一个未溶胀的玻璃态水凝胶高分子材料放于可溶胀介质中，首先溶剂分子渗入高分子材料骨架中，玻璃态高分子材料开始溶胀，溶胀部分的高分子材料由于玻璃化转变温度的降低（如Tg低于溶胀介质温度时）而转变成高弹态，未溶胀部分仍为玻璃态。这种溶胀行为的特性是具有两个界面：一个是处于玻璃态与高弹态之间的界面，称为溶胀界面，其以速率v向玻璃态区移动；另一界面是处于膨胀的高弹态与溶胀介质（即溶剂）之间的界面，它向外移动，从平面几何角度而言，玻璃态区限制了溶胀只能朝一个方向进行，即向内溶胀，这种限制在玻璃态区内产生了一个压缩应力而在高弹态区产生了拉伸张力，一旦这两个溶胀界面会合，玻璃态区将完全消失，高分子材料将转变成高弹态，此时溶胀限制因素消失，溶胀则向三维方向进行。

如载有药物的玻璃态高分子材料与水溶液相接触时，由于溶胀作用，分散于高分子材料中的药物开始向外扩散出来，因此药物的释放同时有两个速度过程：水扩散进入高分子材料过程和链的松弛过程。随着高分子材料骨架的继续溶胀，药物不断扩散出来，药物释放的总速率由高分子材料网络的溶胀速率所控制，即药物释放速度与时间的关系取决于水的扩散速率及大分子链松弛速率。

药物扩散与高分子材料松弛时间的相对重要性可用德博拉数De（Deborah number）来表示，De定义为特性松弛时间（τ）与溶剂的特性扩散时间（t）的比值。

式中L——控释装置的特性长度；

Dw——水的扩散系数。

当De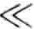1时，说明松弛过程快于扩散，则药物转运符合Fick定律，这种情况出现于当温度高于Tg，凝胶是黏弹态，而且药物的扩散系数是浓度的函数时；当De≈1时，松弛与扩散双重作用导致一种复杂的转运行为，则称之为非Fick扩散。

2.扩散系数

当药物从剂型内向外扩散释放时，由于存在浓度差，药物分子的热运动将向着缩小浓度梯度、趋向平衡的方向进行。在此过程中，对于药物分子质量的转移（即扩散），由Fick第一定律可知，浓度梯度的存在是引起扩散的先决条件，没有浓度梯度就没有扩散。扩散现象描绘了分子或颗粒的直线运动，按照Stokes-Einstein扩散方程，扩散系数为：

式中D0——扩散系数，cm2/s；

η——黏度，Pa·s；

k——玻耳兹曼常数，1.380663×10﹣23J/K；

T——绝对温度，K；

γ——扩散分子的半径，cm。

式（6.1.11）描述由kT/ζ（根据Stokes定律，物质的移动摩擦系数ζ＝6πrη）所产生的分子运动，且受扩散物质性质的制约。由于可能存在限制扩散的屏障，因此该方程无法直接应用于多相环境中。实际中的扩散系数受到药物分子的大小、极性、药物在高分子材料中的溶解度和高分子材料的结构、温度等因素的影响，因此不是一个常数。

药物通过多孔高分子材料的速率与高分子材料多孔网络的曲折度、孔隙的大小、孔隙的分布、药物在孔隙壁上的吸附性质等有关，而药物通过无孔高分子材料时，大分子链之间的距离是影响通过速率的重要因素。在前一种情况下，扩散系数（D）用下式来表示：

式中Da——药物在液体介质（或充满水的孔隙）中的扩散系数，cm2/s；

ε——孔隙率；

τ——曲折因子；

Kp——药物在高分子材料-介质（水）之间的分配系数；

Kτ——限制性系数。

式（6.1.12）中各参数测定的一般方法如下：

（1）Da是在实验条件下药物在纯水中的扩散系数，可按一般物理化学实验法或查表求得，事实上这也是一种假设的条件，因孔道中的药物浓度不断变化，准确测定是相当困难的。

（2）ε可用水银孔隙仪测定。

（3）τ一般为3，但随多孔网络的无序性增加而增加。

（4）Kp可用在已知浓度的药物溶液中浸泡高分子材料的传统方法来测定。

（5）限制性系数Kτ，其平均孔径用水银孔隙仪测定（药物的分子半径可查阅文献或用近似法测定）。

药物通过无孔高分子材料的扩散过程是在大分子链的间隙进行的（其大小约为1～10nm），任何导致扩散屏障增加的形态改变，都会引起有效扩散面积的相应减小以及大分子流动性的下降。对药物扩散系数的控制可以通过控制交联度、支化度、结晶度、大分子晶粒大小及添加助剂来实现。根据高分子材料的溶胀、凝胶和弹性体的性能不同，扩散系数的表示方式也不同，有的仅适于弹性体膜，有些则适于可溶胀的高分子材料。