信道编码器的应用与作用

除了在再生中继协议一章中的几节有所涉及，其余章节并没有考虑外编码器，但在现代通信系统中信道编码器以及各种类型的交织器是经常用到的。如果考虑信道编码器与交织器，那么系统分析和设计会变得相当复杂。但也提出了各种渐近性能的方法，例如，译码器输出端SNR的近似方法：它等于输入端SNR乘以码率和码的自由距离。在文献[580]中介绍了另外一个针对块码和格码的近似方法，我们随后将对此作简单介绍。为了表述方便，我们仅考虑编码的单输入单输出（SISO）系统，假设信道编码采用线性卷积码或者二进制块码，并采用比特级交织技术以避免突发错误所带来的误码，从而能获得平均误比特概率（BEP）。

首先考虑汉明码和格雷码^[278]。硬判译码器输出的误字率（WEP）是译码器输入端未编码BEP的函数，表达式为[278]

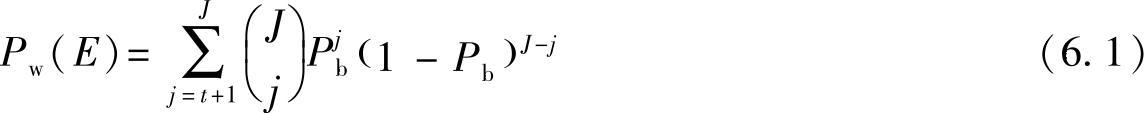
其中，J为码字的比特数；t为码字能够纠正的错误数；d_min是码字的最小汉明距离；P_b为未编码信道的误比特概率，这在第3、4章已经详细介绍了；E为错误事件。考虑到信道编码方案下参数J、t以及d_min的取值如表6.1所示。对于存在信道编码的协同通信，我们最终要关心的是误帧率（PEP）。当一帧数据中至少有一个比特发生错误时，称此帧发生错误。基于理想交织假设，错误在整帧中均匀分布并相互独立，因此在一帧时间内对于所有码字而言WEP都相同。PEP可表示为WEP的函数形式，具体为

其中，N为码字的比特数；k为一个码字的信息比特数。WEP的一种近似为[580]

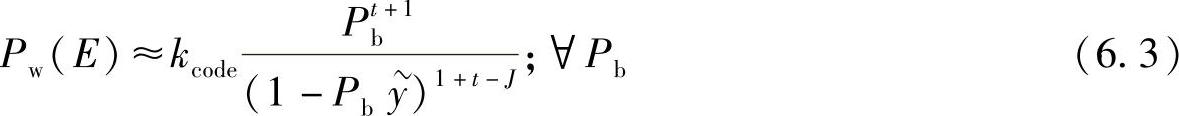
其中，y=（t+1）/（t+2）；k_code是与码相关的常量，具体为

由此可知，由WEP能很容易地推导出BEP，从而推导出编码系统的PEP。

表6.1 汉明码以及格雷码参数设置

接下来考虑卷积码。对于卷积码，首先分析首次错误事件概率（EEP），记为P（E₁），它表示译码格图中在第j步首次偏离正确路径的概率，并假设P（E₁）对于格图中任意位置都相同。EEP的上界^[582]为(www.xing528.com)

式中，T为打孔周期；P_k为汉明距离为k的错误译码序列的概率；a_k为汉明距离为k的权重。如果采用硬判决译码，则对于k≥d_min，P_k可表示为^[583]

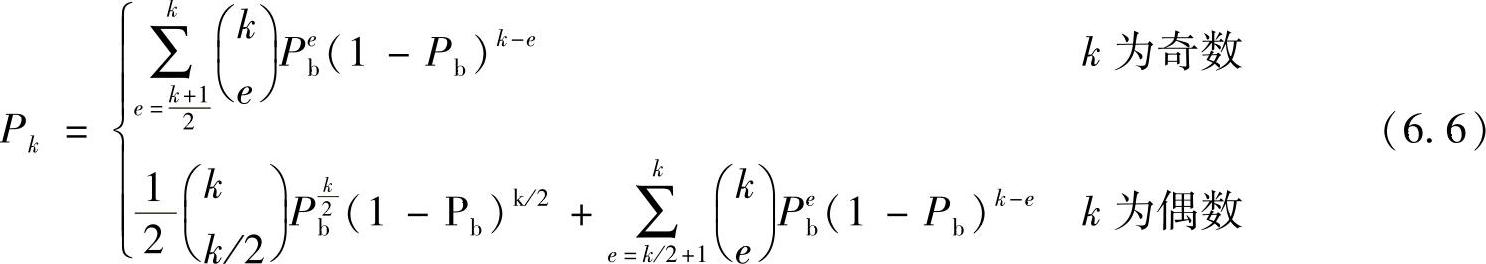
译码器采用Viterbi算法对编码块长为N的码字进行译码，误块率表示Viterbi译码输出的似然序列与原始信息序列不同的概率。似然序列在格图的第j步偏离正确路径的概率上界由式（6.5）给出，如果假设格图任何地方出错的概率都相同，那么PEP的上界为

同样，上式的一个有效的近似在文献[580]中给出，其中利用了EEP的近似表示^[584]

其中，首次错误事件概率的近似表达式为

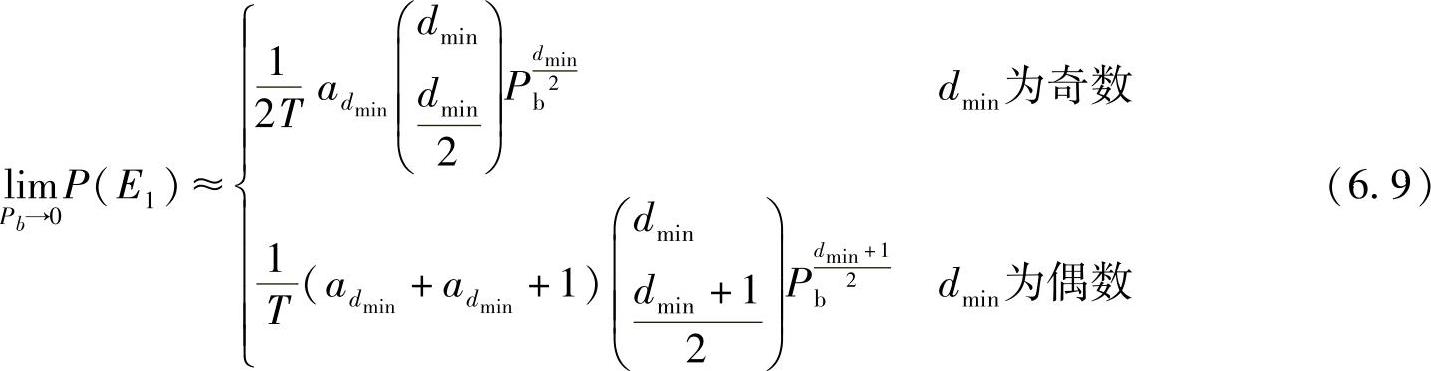
式中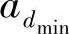，表示具有最小汉明距离d_min的路径数。当时，P_b→0，PEP可表示为译码器输入序列的未编码BEP的幂。表6.2总结了两种卷积码的PEP渐进表达式，这两种卷积码假设都没有打孔，即T=1。由此也可见本书推导的错误率能够很容易地应用于上述编码错误率的表达式之中。

表6.2 两种卷积码的PEP近似表达式，编码器参数中，约束长度分别为K=4，K=7；生成多项式分别为（15，17）8，（133，171）8