网络编码的分复用技术优化

在上节中介绍了无线中继网络中基于图码的分布式网络信道编码（DNCC）方案。DNCC能获得可观的编码增益，然而它只适用于多源节点构成的单源节点群与单个目的节点通信的多址接入中继信道（MARC）。很多无线网络中，多个源节点群通过公共的中继网络分别同时与多个目的节点通信，这种场景称为多址接入中继干扰信道（MARIC）。MARIC的典型应用是智能测量网络，其中所有水表与水源数据管理中心通信，而所有电表与电能中心通信，所有这些传感器（水表或电表）共享同一个无线中继网，因而在目的端将存在相互干扰。

本节介绍基于网络编码的多接入复用方案，即针对MARIC的分布式网络信道编码（DNCC）方案，在获取网络和信道编码增益的同时，还能使得多个源节点群能够相互独立地与多个目的节点进行通信。在DNCC-MARIC中，每个中继进行线性网络编码操作，在目的节点处自然构成图码。为消除目的节点处存在的源节点群之间的相互干扰，我们提出一种码零陷算法，用于实现多个源节点群与多个目的节点同时通信且消除相互间的干扰。仿真结果表明，在MARIC信道下DNCC能获得与MARC信道下相同的误码性能，但大大提高了网络吞吐量。

4.4.2.1 系统模型

为简单起见，考虑由两个分别记为Ω_A与Ω_B的由源节点群A与B构成的MARIC系统，其系统模型如图4.77所示。群A中所有的源节点都只与目的节点d_A通信，而群B中所有源节点只与目的节点d_B通信，但两个群共用一个中继网络。我们设计一种分布式编码方案，使得同一个群组的节点在与目的节点通信时不受到其他源节点群的干扰。

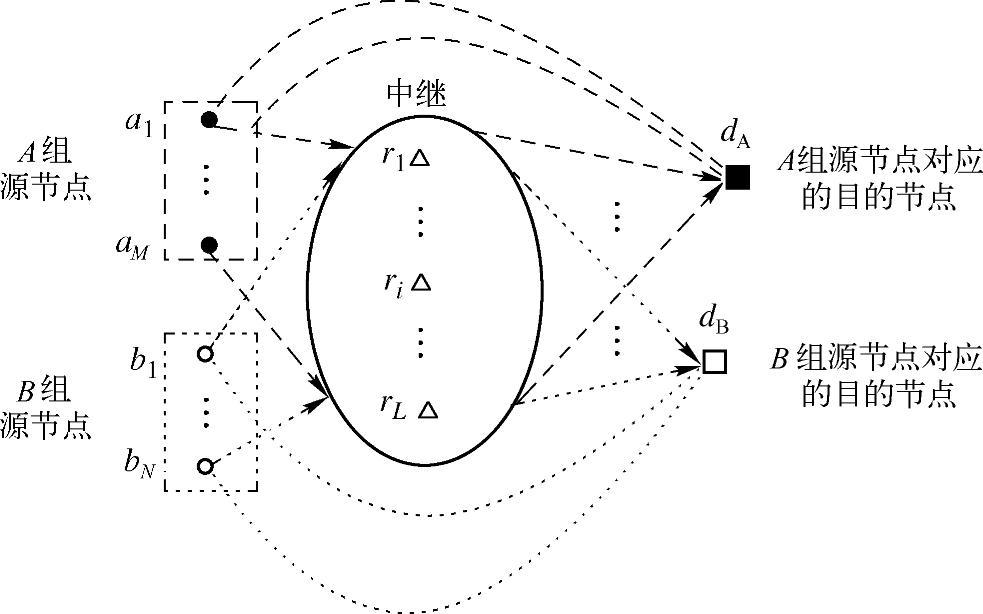
图4.77 多接入中继干扰信道

假设群A中有M个源节点a₁，…，a_M，群B中有N个源节点b₁，…，b_N，以及L个中继r₁，…，r_L，且所有节点通过正交信道传送信息。令A_i与B_j分别表示源节点a_i与b 发送的信息比特，A=（A₁，…，A_M）与B=（B₁，…，B_N）分别表示群A中M个节点与群B中N个节点发送的信息比特序列。

最初所有源节点将其信息广播至中继和目的节点。与DNCC类似，所有中继从成功检测的信号中随机选择若干比特，通过模二加运算产生一位奇偶校验比特。来自源节点群以及中继的信号在目的节点处自然构成一个图码，这就是4.4.1节中介绍的DNCC。

图码可用二分图表示，在目的节点d_A和d_B处形成的二分码图都由M+N个变量节点与L校验节点构成，分别对应于M+N个源节点与L个中继上的奇偶校验方程。图4.78与图4.79的左半部分示意了M=N=3，L=4的MARIC系统中在目的节点d_A和d_B处生成的二分图。用C_A和C_B分别表示节点d_A和d_B处生成的图码，G_A和G_B分别表示相应于图码C_A和C_B的生成矩阵。根据矩阵A和B的维度，G_A和G_B可表示为如下的块矩阵：

其中，N_row（G_A，1）=N_row（G_B，1）=N_col（A）=M，N_row（G_A，2）=N_row（G_B，2）=N_col（B）=N，而N_col（X）和N_row（X）表示矩阵X的行数和列数。设D_A=（D_A¹，…，D_A^M+N+L）与D_B=（D_B¹，…，D_B^M+N+L）表示C_A与C_B中的码字，则有

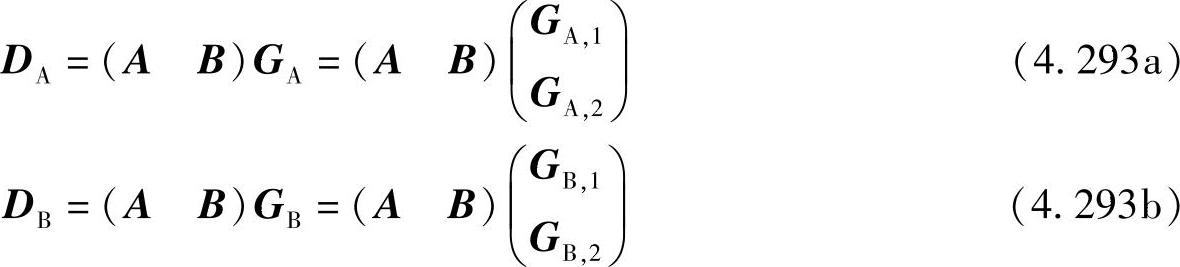
从式（4.293a）可知，d_A和d_B的接收码字D_A和D_B是A与B的线性组合，这意味着来自群A与群B的信号在目的节点接收时相互干扰。显然我们希望d_A仅接收来自群A的信息，d_B仅接收来自群B的信息，因此我们试图提出一种在抑制群间干扰的同时能获得网络信道编码增益的编码方案。

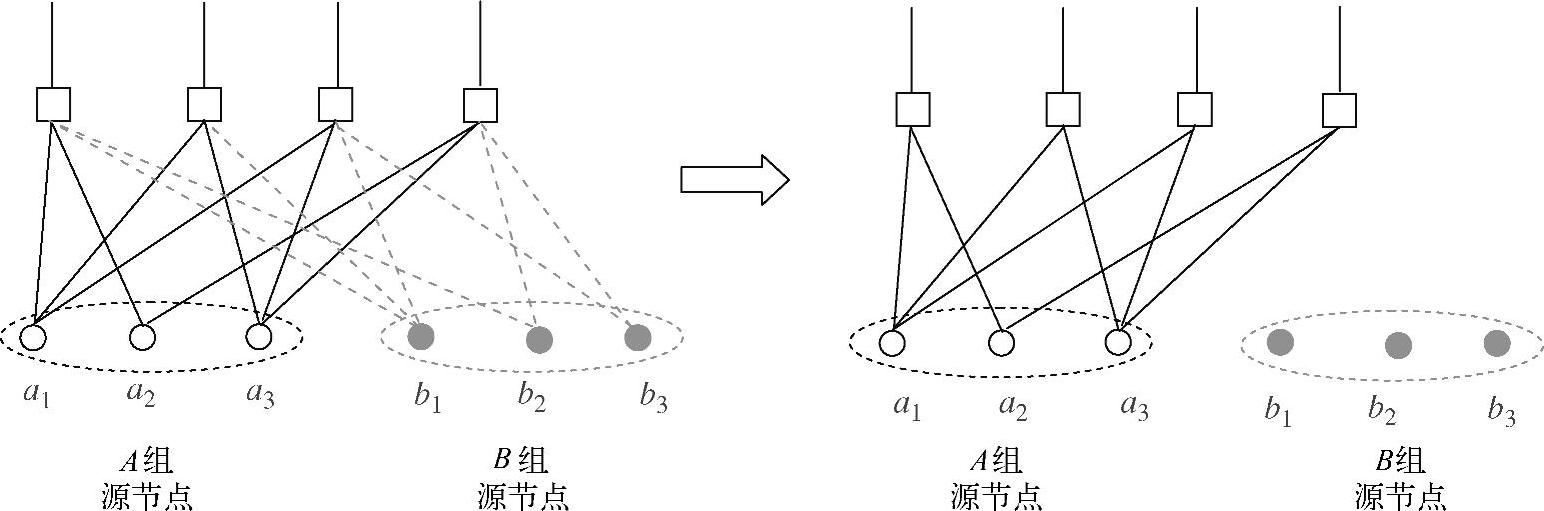
图4.78 目的节点d_A码零陷处理前后的二分图

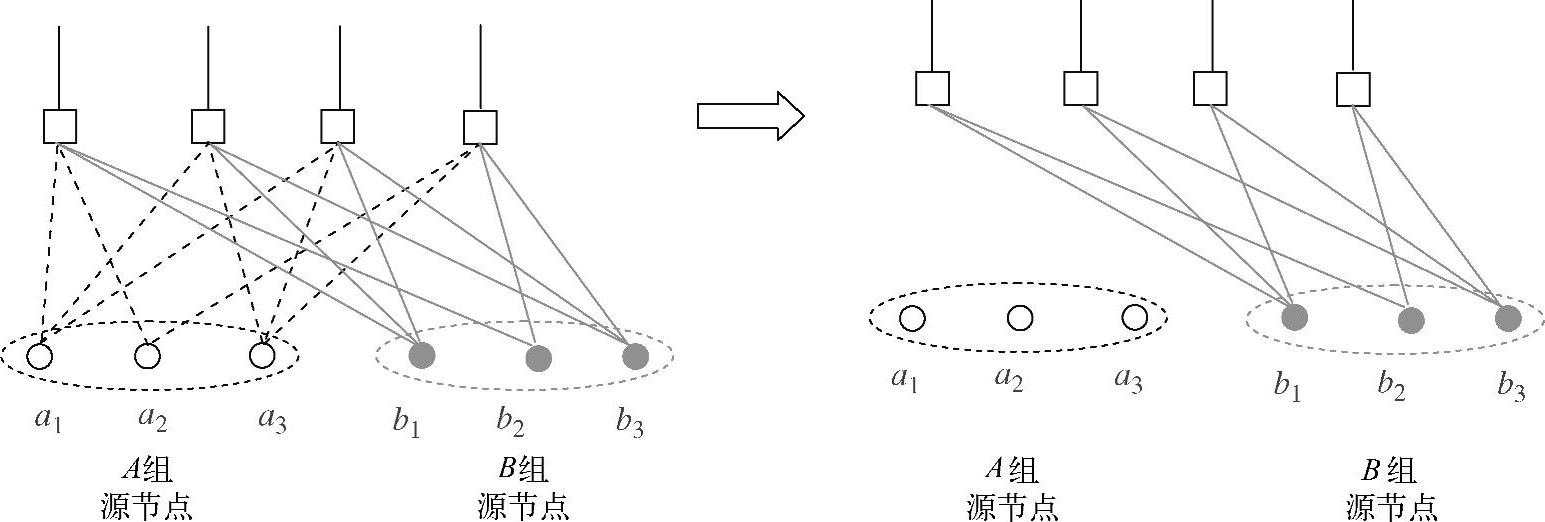
图4.79 目的节点d_B码零陷处理前后的二分图

4.4.2.2 网络编码分复用

本节介绍基于网络编码的多接入码分复用方案，该方案实现了通过MARIC系统同时传输相不干扰的信号向量A和B。

使用式（4.293a）和（4.293b）所示的块矩阵公式，可进一步把每个块码分成两个子码。即把由G_A产生的码C_A拆分为C_A，1与C_A，2两个子码，这两个子码分别由G_A，1与G_A，2生成。同样把由G_B产生的码C_B拆分为由G_B，1与G_B，2生成的C_B，1与C_B，2两个子码。设H_A，2和H_B，1分别为G_A，2和G_B，1的奇偶校验矩阵，则可得到如下等式：

应用以上两个等式可得

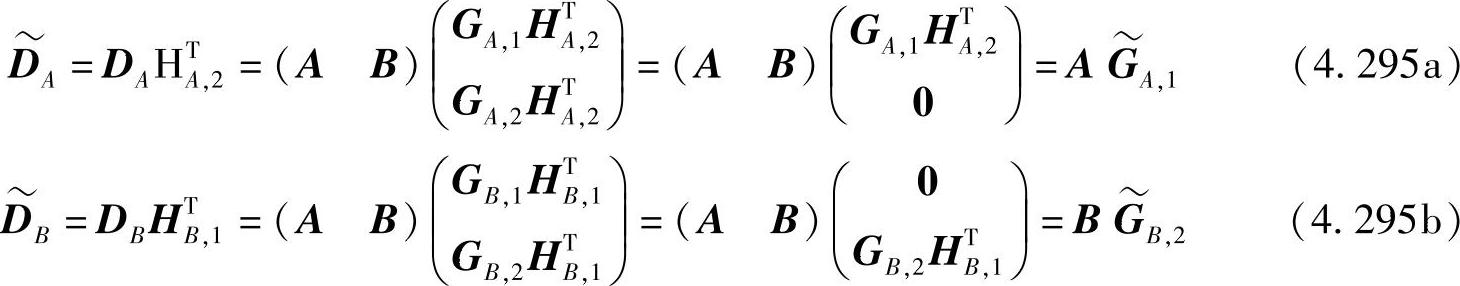(www.xing528.com)

其中

由式（4.296a）和（4.296b）可以看出，对接收码字D_A右乘校验矩阵H^T_A，2可得到目的节点d_A的新码字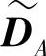，其等效的生成矩阵为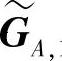1。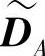不仅是A的码字而且不包含来自B的干扰。同样，目的节点d_B对接收到的码字D_B右乘校验矩阵H^T_B，1之后得到一个新的码字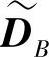，其等价的生成矩阵为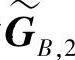。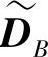不仅是B的码字而且消除了来自A的干扰。

通过上述处理，整个网络分解成了两个相互独立的网络，其传输矩阵分别为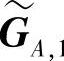和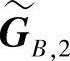，从而完全消除了群间干扰。我们称这种处理方法为码零陷技术。码零陷技术把MARIC转化为两个独立的多接入中继信道（MARC），每个MARC都由一个源节点群与一个与之通信的目的节点构成，并且同一时刻两个源节点群分别与两个目的节点通信，却不存在相互干扰。也就是说，码零陷技术把维度为（M+N+L，M+N）的两个线性块码C_A与C_B转化为两个独立的线性块码：（M+L，M）维的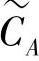与（N+L，N）维的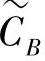，其生成矩阵分别为和产生。码零陷处理流程如图4.80所示。

为了简化，进一步假设C_A和C_B是系统图码，譬如低密度生成矩阵（LDGM）码，于是可得

以及

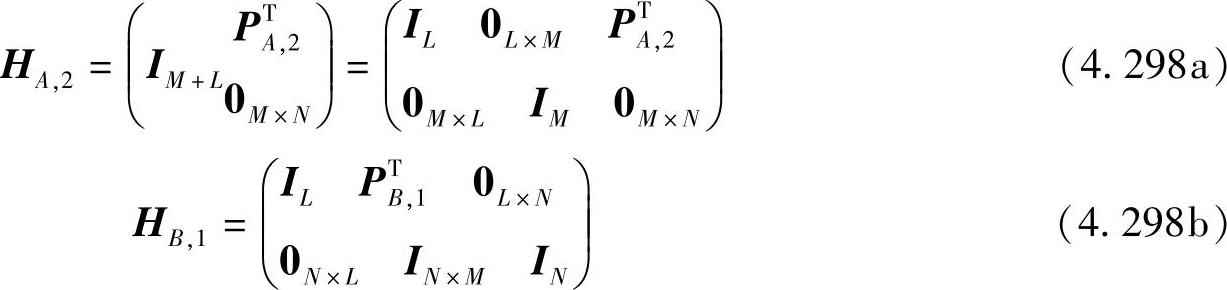
将式（4.298a）和式（4.298b）代入到式（4.296a）和式（4.296b）中，得到

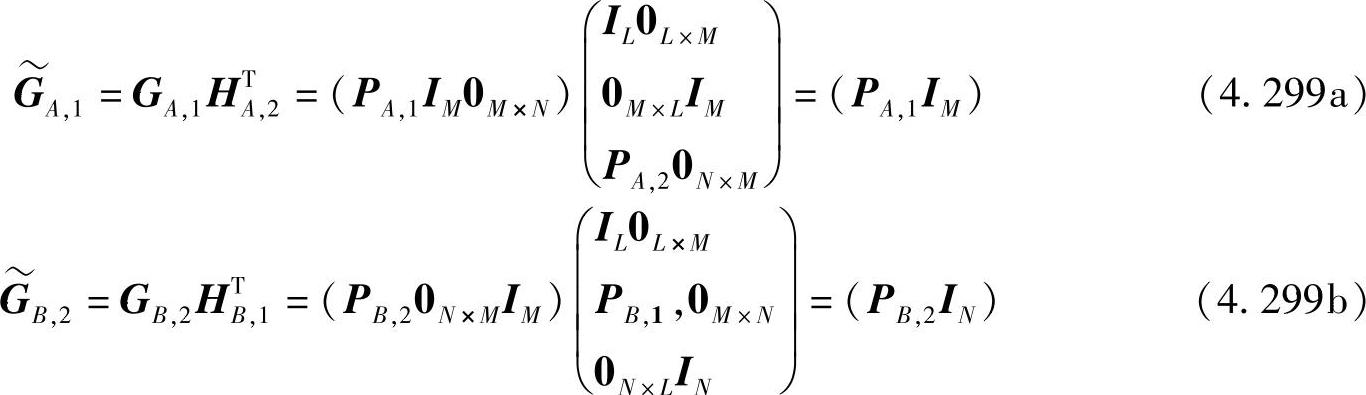
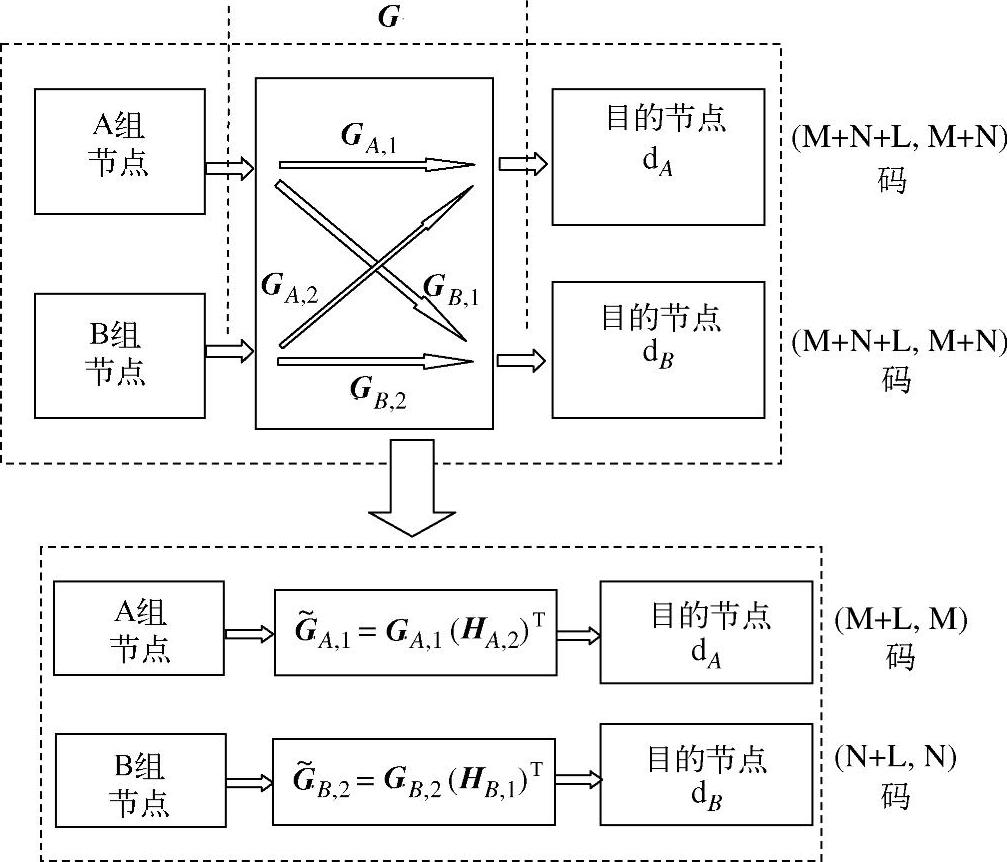
图4.80 利用码零陷把MARIC分解为两个MARC

从上两式可以看出，目的节点d_A对群A进行码零陷处理后，除了一些零矩阵，等价的生成矩阵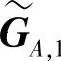与码零陷处理之前的生成矩阵G_A，1本质上相同。群B节点也一样。因此，对应于各个源节点群的二分图码在码零陷编码前后本质上相同，目的节点d_A和d_B在码零陷前后的二分图如图4.78和图4.79所示。我们称这种变换处理不改变生成矩阵的性质为变换恒定性。因此，对于每个源节点群任意的码生成矩阵，两个源节点群之间将不会彼此干扰，这对于放宽系统设计要求极具意义，因为在分布式图码设计时可以仅考虑本源节点群而无需考虑其他源节点群。

在上述处理时，假设目的节点对D_A和D_B进行硬判决。为了能使用置信传播算法对新码字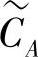进行译码，目的节点d_A必须计算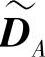的对数似然比（LLR）信息，但是d_A仅知D_A的对数似然比信息。由式（4.295a）可见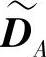，是D_A的二进线性变换，其对数似然比可利用下述定理进行计算。

定理4.4.1 设L（b_kj）为信息比特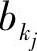的对数似然比，那么序列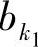，…，的二进线性和的对数似然比为

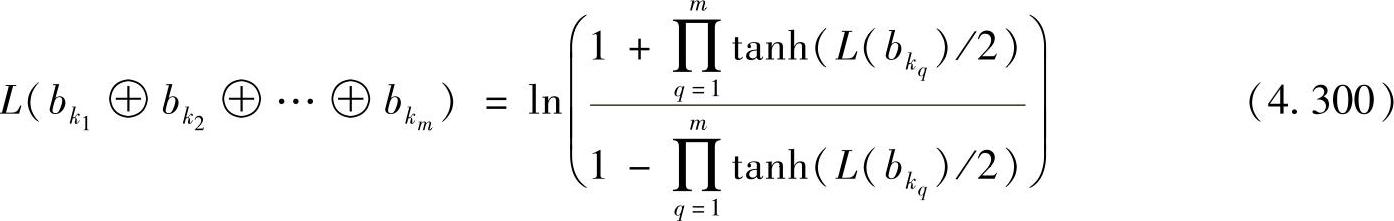
其中，。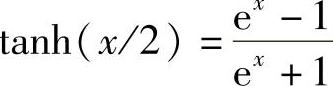

4.4.2.3 仿真结果

本节仿真评估MARIC中DNCC的性能。设在目的节点处形成的图码为系统LDGM码，任意两节点间信道要么是AWGN信道，要么是瑞利衰落信道，并且所有节点的发射E_b/N₀相同，其中E_b为信息比特能量。仿真系统中两个源节点群各由500个传感器节点构成，分别与两个目的节点通信，并有1000个中继。图4.81比较了MARIC与MARC的BER性能，中继节点的维度为4。从仿真结果图可以看出，AWGN信道下，采用DNCC技术的MARIC具有与MARC大致相同的BER性能，这意味着DNCC几乎能够完全抑制群间干扰。而在瑞利衰落信道下，MARIC的性能比MARC稍差，这是因为使用D_A的对数似然比来计算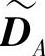的对数似然比。随着中继节点维度的增加，采用DNCC的MARIC与MARC之间的性能差也随之增加，这是因为用D_A的对数似然比来计算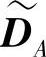的对数似然比产生的误差随着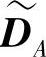维度的增加而增大。然而，在此例中，MARIC的吞吐量相比MARC提高了50%。图4.81还比较了DNCC与重复码方案之间的BER性能，其中重复码方案是指每个源节点的发送信息在每次传输中仅被转发一次。图示的仿真结果验证了DNCC相比重复码方案能获得显著的编码增益。

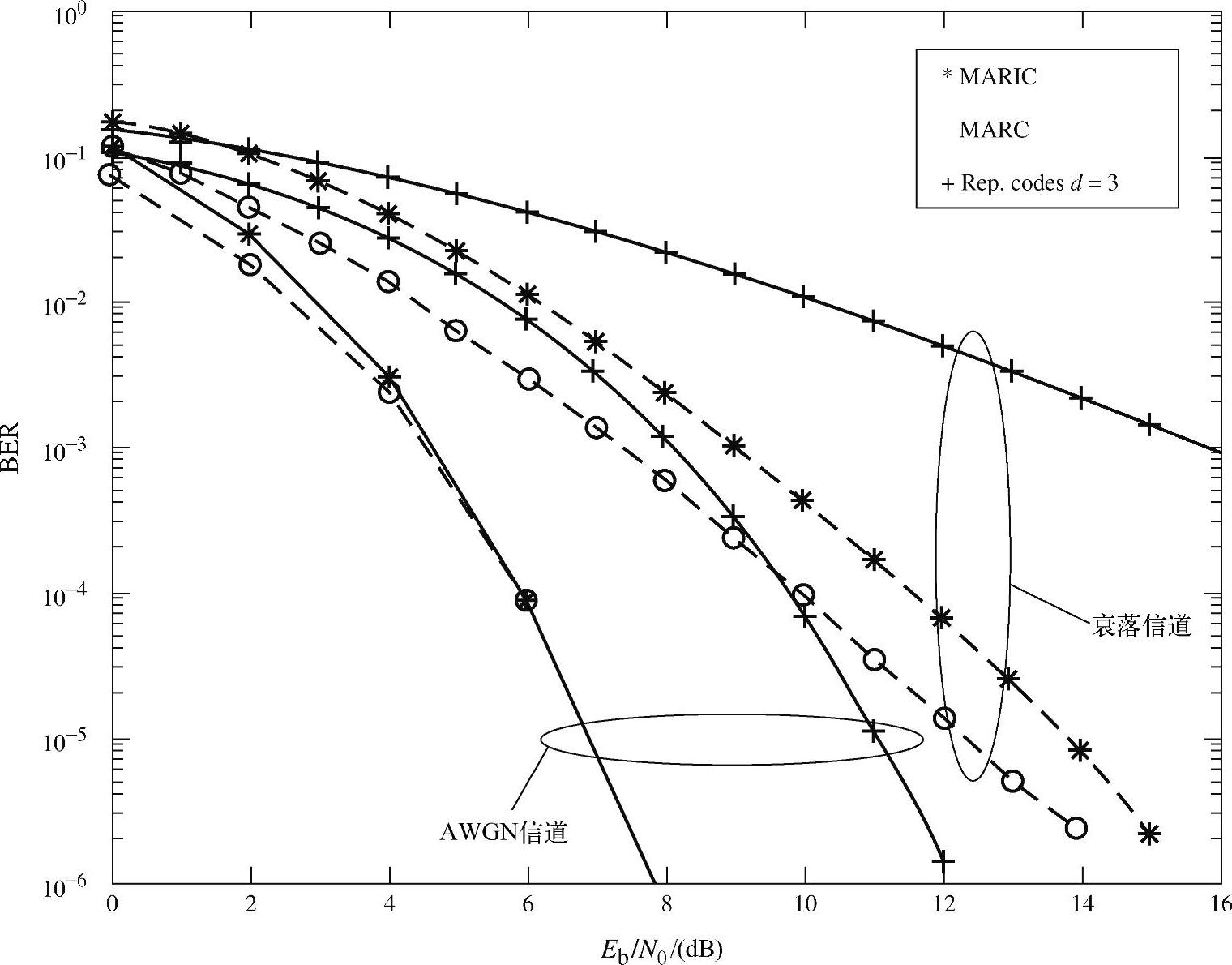
图4.81 BER性能对比