分布式网络信道编码分析介绍

之前讨论的分布式编码方案都是针对两跳结构的单播中继网络，即信息从一个源节点经一个或多个中继传输至一个目的节点。这种方式的分布式编码方案难以扩展到更一般的多跳中继网络之中，且不能够随着跳数的增加和网络规模的增大而扩展。那些基于传统空时编码或Turbo编码的分布式编码方案只能应用于固定的且预先确定的编码格图结构，并且仅能选用种类受限的分量码。上述这些限制使得这些分布式编码方案只适用于规模很小且静态的网络拓扑结构。而在无线网络中，任意两个节点之间的信道都受到衰落和噪声的干扰，且当某些链路失效时，网络的物理层拓扑结构将会发生改变。尽管上节介绍的广义分布式Turbo码（GDTC）在一定程度上可以随着网络拓扑的变化而实时调整，但Turbo码方案的内在属性决定了它只适用于两跳中继网络。

本节我们将分布式编码设计从简单的两跳中继系统扩展到具有时变网络拓扑的一般中继网络中。近年来提出的网络编码技术通过简单的编码与路由处理可有效提高网络的频谱效率^[500]。网络编码最初是针对于无损网络，并能达到无损中继网络的最大吞吐量。最近，在无损中继网络中通过合理设计网络编码，可以为数据帧传输提供较强的差错保护^[501]。无线信道的广播特性非常适合使用网络编码，在无线中继网络中已有联合设计网络编码与信道编码的方案^[502-505]，我们称之为分布式网络信道编码（DNCC）。

在本节中，我们将介绍适用于一般的无线中继网络的分布式网络信道编码方案，其信道编码基于一般的图码，例如低密度生成矩阵码（LDGM）、低密度奇偶校验码（LDPC）等。我们首先简要介绍图码及其译码算法，然后介绍基于图码的分布式网络信道编码方案，最后通过计算机仿真评估其性能。

4.4.1.1 LDPC码介绍

在介绍基于图码的DNCC方案之前，首先简单介绍LDPC码及消息传递译码算法。

最早由Gallager在1963年提出的LDPC码^[506]是二进制线性分组码中的一类好号码，它是由‘1’的数目非常少且随机分布的稀疏校验矩阵所定义。当时由于计算机的处理能力限制仅考虑短码，直至近年来‘重发现’LDPC码时才注意到其具有逼近信道容量限的纠错性能^[507，508]。

LDPC码由校验矩阵定义。对于规则LDPC码，校验矩阵中每列‘1’的个数都为γ，每行‘1’的个数都为ρ，并有γ＜ρ且都远小于码长n。对于非规则LDPC码，校验矩阵中‘1’的个数依然很少，即表现出稀疏特性，但行与列中‘1’的个数不再保持相等。

Gallager（n，γ，ρ）LDPC码是规则LDPC码，其码长为n，校验矩阵H具有固定的行重ρ和列重γ。H的列数等于码块长度n，行数等于校验符号数，其中k是信息长度，不等号“≤”表示H的行可能不独立。码率为R≥1-γ/ρ，“稀疏”表示γ和ρ相比于n都非常小。Gallager LDPC码的一个实例如图4.65所示，表征的是（20，3，4）LD-PC码的校验矩阵，该校验矩阵可分成3个子矩阵，每一个子矩阵的列都只包含一个“1”。第一个子矩阵看起来像是一个压扁的单位阵，即将单位阵对角元素的“1”用ρ个“1”代替，然后相应地增加ρ倍的列。后面的子矩阵则是将第一个子矩阵的列的位置进行重排。

图4.65 Gallager（20，3，4）码的奇偶校验矩阵

LDPC码也可以用二分图表示：假设校验矩阵H的行向量相互独立，二分图的一边用n个圆圈表示变量节点，它表示码字长度；另一边用n-k个方框表示校验节点，代表j个校验方程。由校验矩阵可以很直观地得到相应的二分图：如果校验矩阵的第（i，j）项为1，则将二分图中的第j个变量节点与第i个校验节点用直线相连。以（7，4）汉明码为例，其校验矩阵如图4.66所示，则相应的二分图如图4.67所示。

图4.66 （7，4）汗明码的奇偶校验矩阵

图4.67 （7，4）汗明码对应的二分图

LDPC码的译码可基于二分图。在译码过程的每次迭代时，消息从变量节点传递至校验节点，也从校验节点传递到变量节点，因此形象地称这一算法为消息传递译码算法（MPA）。码图的稀疏性可以实现高效的译码算法。和积（sum-product）算法是消息传递算法的一个重要子类，其译码过程包括初始化、迭代更新和判决三个步骤：

1.初始化

设X=（x₁，…，x_n），x_i∈{-1，1}表示发送的码字，r=（r₁，…，r_n）表示经过衰落信道加扰后的接收信号。码字中每个比特的信息初始化为

然后将校验矩阵H的第i列的所有非零项赋值为Δ_i，从而得到新矩阵J，此时J矩阵的同一列中所有非零项Δ_ji具有相同的初始值Δ_i。

2.迭代更新

迭代处理过程包括水平更新阶段和垂直更新阶段。在水平更新阶段，译码器更新从校验节点j到变量节点i的似然比信息为

其中，N（s_j）表示所有与校验节点j相连的变量节点的集合，即校验矩阵H中第j行中有“1”的所有列；N（s_j）\x_i是所有与校验节点j相连的且不包括变量节点i的所有变量节点的集合。在水平更新阶段，译码器更新所有从变量节点i到校验节点j的似然比信息为

对于每一个变量节点i，伪后验概率的计算如下：

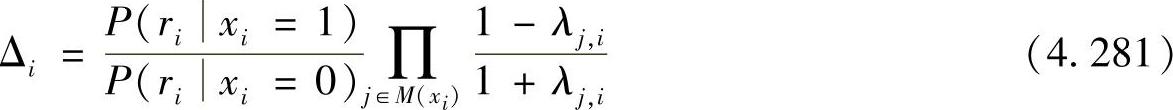
其中，M（x_i）是与变量节点x_i相连的校验节点的集合，即H的第i列中所有含有“1”的行，M（x_i）\s_j是M（x_i）中除去校验节点s_j之后的集合。

3.判决评估

根据估计值Δ_i译码器尝试译码：

如果满足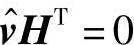，则译码过程停止，并认为是有效的码字，否则译码器进行迭代更新处理。当到达最大迭代次数依然不满足校验方程时，则认为译码失败。

图4.67所示的汉明码的和积译码过程中的信息传播示意如图4.68所示。

图4.68 图4.67所示的汗明码的和积译码过程

4.4.1.2 自适应网络编码协同

为获得最佳的无线系统性能，需要对网络编码和信道编码进行联合编码设计。本节将介绍基于图码的分布式网络信道编码的基本原理。基于图码的DNCC方案最早由Bao和Li提出[504]，被认为是一种自适应的网络编码协同方案（ANCC），其基本思想是把基于图的编码和基于图的网络进行匹配。

在ANCC中，节点之间通过无线链路进行通信。如图4.69所示，假设有M个源节点S₁，…，SM，L个中继节点r₁，…，r_L。所有节点在相互正交的信道上发送信号。首先每一个源节点都广播其信号至其他源节点、中继以及目的端。接收到其他节点发送的信号后，每个中继对每一个接收信号进行译码。假设中继r_i对来自源节点集合D（i）⊂{S₁，…，S_M}的信号可以正确译码，则此源节点集合称为中继r_i的译码集合。中继从其译码集合中随机选择子集T（i）⊂D（i），并对相应的译码信号在GF（2）域上进行模2加运算，得到一个校验比特。称子集T（i）为中继r_i的网络编码子集。通过中继上的编码操作，目的节点可获得LDPC码或是LDGM码之类的图码。

为了更进一步解释ANCC的基本原理，考虑由4个源节点和5个中继构成的中继网络，假设在每一时隙只有一个节点（源或中继）发送数据，图4.70所示的网络图描述了该网络在某一时刻的瞬时拓扑，其中实心点表示源节点，空心点表示中继节点，虚线表示中继与其译码集合中的源节点的虚拟连接，即表示沿该链路发送的信号在此时刻可以被中继正确译码。例如，由图可见，r₁的译码集合包含源节点S₁和S₃，即D（1）={S₁，S₃}。同样有D（2）={S₁，S₂，S₄}，D（3）={S₂，S₃}，D（4）={S₁，S₄}，D（5）={S₂，S₃，S₄}。

图4.69 普适的多址接入中继网络

(www.xing528.com)

图4.70 中继网络的瞬时网络拓扑结构

因为网络拓扑随时间而变化，因此每个中继的译码集合及其虚拟连接也将随着时间而变化。下面以图4.70所示的网络图为例介绍ANCC的原理。设b_s，i（k）是源节点S_i发送的第k个比特，并假设源节点和中继节点按照其下标的次序依次发送，即：在前4个时隙，4个源节点S₁，…，S₄顺序发送信息至中继和目的节点，每个中继对接收到的信号进行译码，被中继r_i正确译码的源节点被划入译码集合D（i）。在图4.70所示的网络图中，只有那些和某一中继有虚拟连接的源节点发送的信号可以被该中继成功译码。

中继i从其网络编码子集T（i）⊂D（i）中随机地挑选符号，并进行GF（2）域上的模二加操作，得到校验信息后转发至目的节点。为了更清楚地理解网络图如何与码图进行匹配，首先考虑T（i）=D（i）的情况。设b_r，j（k）是中继r_j发送的第k个比特，基于图4.70所示的网络图，中继r₁能够正确地恢复比特b_s，1（k）和b_s，3（k），因此中继r₁转发的校验比特为b_r，1（k）=b_s，1（k）⊕b_s，3（k）。类似地，可得到b_r，2（k）=b_s，1（k）⊕b_s，2（k）⊕b_s，4（k），b_r，3（k）=b_s，2（k）⊕b_s，3（k），b_r，4（k）=b_s，1（k）⊕b_s，4（k），b_r，5（k）=b_s，2（k）⊕b_s，3（k）⊕b_s，4（k）。

在随后的5个时隙里，5个中继节点r₁，…，r₅顺序发送b_r，1（k），…，b_r，5（k）。目的节点在前4时隙接收到来自源节点的4个信息符号，在随后的5个时隙接收到来自中继的校验符号，信息符号和校验符号构成一个完整的LDGM码字C。令G表示C的校验矩阵，D（k）=（d₁（k），…，d₉（k））=（b_s，1（k），b_s，2（k），b_s，3（k），b_s，4（k），b_r，1（k），b_r，2（k），b_r，3（k），b_r，4（k），b_r，5（k））表示码字C中相应于源符号B_s（k）=（b_s，1（k），b_s，2（k），b_s，3（k），b_s，4（k））的码字，这可进一步表示为

D（k）=B_s（k）G （4.284）

其中

由于是系统码，其校验矩阵可以表示为

根据式（4.286）所表示的校验矩阵，相应的二分图如图4.71所示，它与图4.70所示的网络图相匹配。获得码图后，可采用传统的信息传递译码算法进行迭代译码，从而恢复源信息。

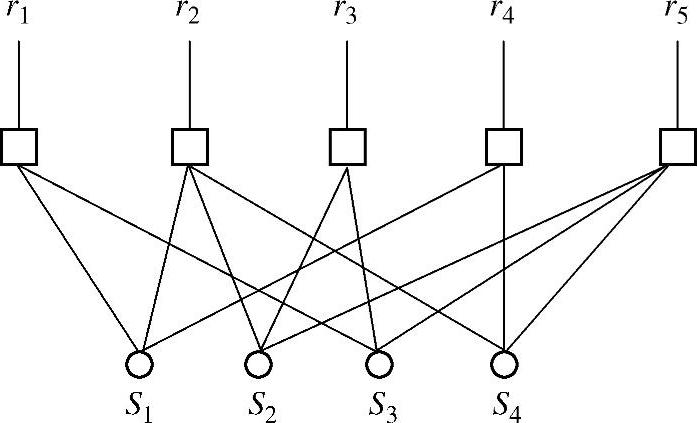
图4.71 与图4.70所示网络图相匹配的二分码图

然而，随着源节点数目的增加，如果每个中继对所有的可以正确译码的比特进行校验操作，那么分布式编码的变量节点和校验节点的维度将会很大，从而显著增加译码的复杂度。同时，随着节点维度的增加，生成短回路的概率也随之增加，这将显著降低系统的性能。为了降低译码复杂度并有效译码，需减少节点维度。为减少节点维度，中继r_i只是随机地从其网络编码子集T（i）⊂D（i）中选择符号并进行校验求和操作，从而简化码图^[504]。例如在图4.70中，中继r₂和r₅在计算校验信息时丢弃来自信源S₁和S₂的符号，此时各中继的网络编码子集分别为：T（1）={S₁，S₃}，T（2）={S₂，S₄}，T（3）={S₂，S₃}，T（4）={S₁，S₄}，T（5）={S₃，S₄}。简化后的码图如图4.72所示。

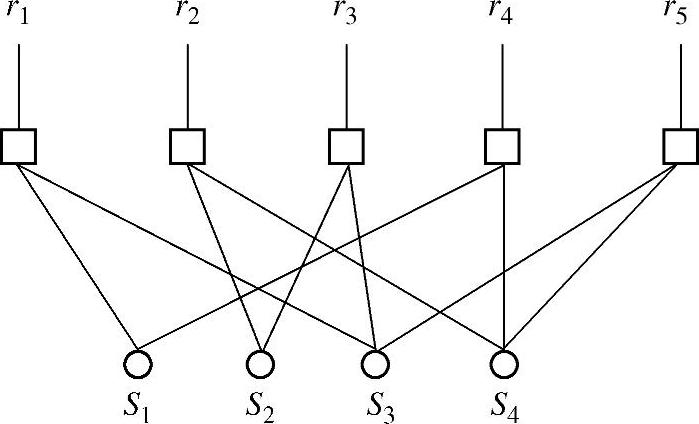
图4.72 简化后的二分码图

通常由M个源节点、L个中继构成的中继网络中，基于LDGM码的ANCC的校验矩阵可以表示为

H=[P^TI_L] （4.287）

其中，P^T是L×M维稀疏矩阵；I_L是L×L维单位矩阵。在每次传输中，目的节点处形成的分布式LDGM码是一个时变码，即不同时刻的校验矩阵也不同，从而有不同的LDGM码。如果中继r_i对其网络编码子集T（i）进行约束，使网络编码符号的维度不超过特定的维度D，这样得到的LDGM码就构成了D维LDGM码集。

现在考虑更一般的多跳网络，其中每个中继不仅转发源节点的信息，同时也转发其他中继的信息。图4.73示意了这样一个例子：中继r_i的译码集合不但包含源节点，也包含在其之前发送信息的中继r_j，j＜i。例如，中继r₄的网络集合不但包含源节点S₁、S₄，也包含中继节点r₁和r₃。与基于LDGM的ANCC类似，该图码相应的校验式为

其中，P_tri是下三角矩阵。需注意的是，相对于LDGM码，上式的右半部分是下三角矩阵，且主对角元素都为1，这种码也称为下三角LDPC码^[504]。相应的二分tanner图如图4.74所示。同样可根据具体的网络拓扑构造相应的LDPC码。

图4.73 描述瞬时网络拓的躲多跳网络图示例

图4.74 与图4.73所示的网络图相对应的二分码图

在实际系统中，为了能对LDGM码或LDPC码进行译码，目的节点必须知道码图。为了辅助目的节点确定码图，每个源节点需要在数据符号前加上信头。对于一个有M个源节点的中继网络而言，每个源节点在发送K个数据符号之外还需额外发送M个信头。设源节点S_i发送的信号X_i为

其中，b^h_s，i=（b^h_s，i（1），…，b^h_s，i（M））和b^d_s，i=（b^d_s，i（1）…，b^d_s，i（K））分别表示b_s，i的信头和数据。M个源节点发送的信号矢量用矩阵形式表示为

其中，B_s^h=（（b^h_s，1）^T，…，（b^h_s，M）^T）^T，B^d_s=（（b^d_s，1）^T，…，（b^d_s，K）^T）^T。

令D表示目的节点处对应于源节点信号B_s的LDGM码字，G表示对应于LDGM码字的生成矩阵，则有

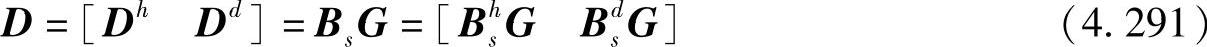
其中，D^h=B_s^hG和D^d=B_s^dG分别表示接收码字的信头和数据部分。由此可见，如果令B^h_s=I_M，则有D^h=G，目的节点就可很容易地获知LDGM码的生成矩阵，从而得到对应的码图。很明显，发送信头需占用系统资源。如果有K＞＞M，即编码块长度远大于信头长度，那么信头所占用的资源可以忽略不计。需指出的是：生成分布式LDGM码或是LDPC码无需中继间的协同，因此可以随机选择源符号从而生成校验比特。可能出现某些源信息没有包含在任何校验信息中的情况，即源信息所对应的校验矩阵的列为全零向量，这些源信息没有被任何校验信息所保护，从而可能影响系统的性能。此外，这些分布式图码是以分布式方式构造的，可能存在相当数量的短回路，这也将会影响系统性能。为了解决这些问题，可引入若干规则以确保每个源节点发送的信息符号至少包含在一个校验式中，并消除短回路。如何设计这样的集中式或分布式机制对于实际系统有着重要的意义，但这至今仍是一个有待解决的课题。

4.4.1.3 仿真结果

本节仿真评估ANCC的误码性能。考虑由1000个源节点、1000个中继和1个目的节点构成的无线传感器网络。源节点发送的数据包都添加了CRC校验，中继译码后通过CRC校验确定是否正确译码，如果CRC校验正确，数据包被保留，否则被丢弃。每个中继对其网络编码子集进行网络编码后转发至目的节点。来自源节点和中继的信号构成LDGM码字。假设每个源节点发送的信息包含在至少一个校验式中，因此校验矩阵中不存在全零列，但并不能完全消除短回路，因此LDGM码图中还将存在短回路。我们仍然假设网络中所有节点具有相同的发送信噪比。

图4.75和图4.76分别给出了AWGN信道和瑞利衰落信道下基于不同维度的LDGM码的ANCC方案的BER性能，这是通过100000次蒙特卡洛仿真实验得到的平均结果。系统LDGM码的码率为1/2。与此相比，我们同样给出了重复码的误码率性能。从仿真结果可见，ANCC性能明显优于基于重复编码的分布式方案，其性能的提升来自于ANCC的编码增益。

一般认为，LDPC类码的度分布对系统的性能具有重要影响。度分布对系统性能的影响也可从仿真结果图中看出。需要指出的是，在误码平层和瀑布区性能之间存在折中：相比于具有高的度分布的码字，具有低的度分布的码字有较好的瀑布区性能，但误码平层较高。因此在实际应用中需要选择合适的度分布以确保获得理想的误码率平层的同时也得到较好的瀑布区性能。

图4.75 AWGN信道下ANCC性能

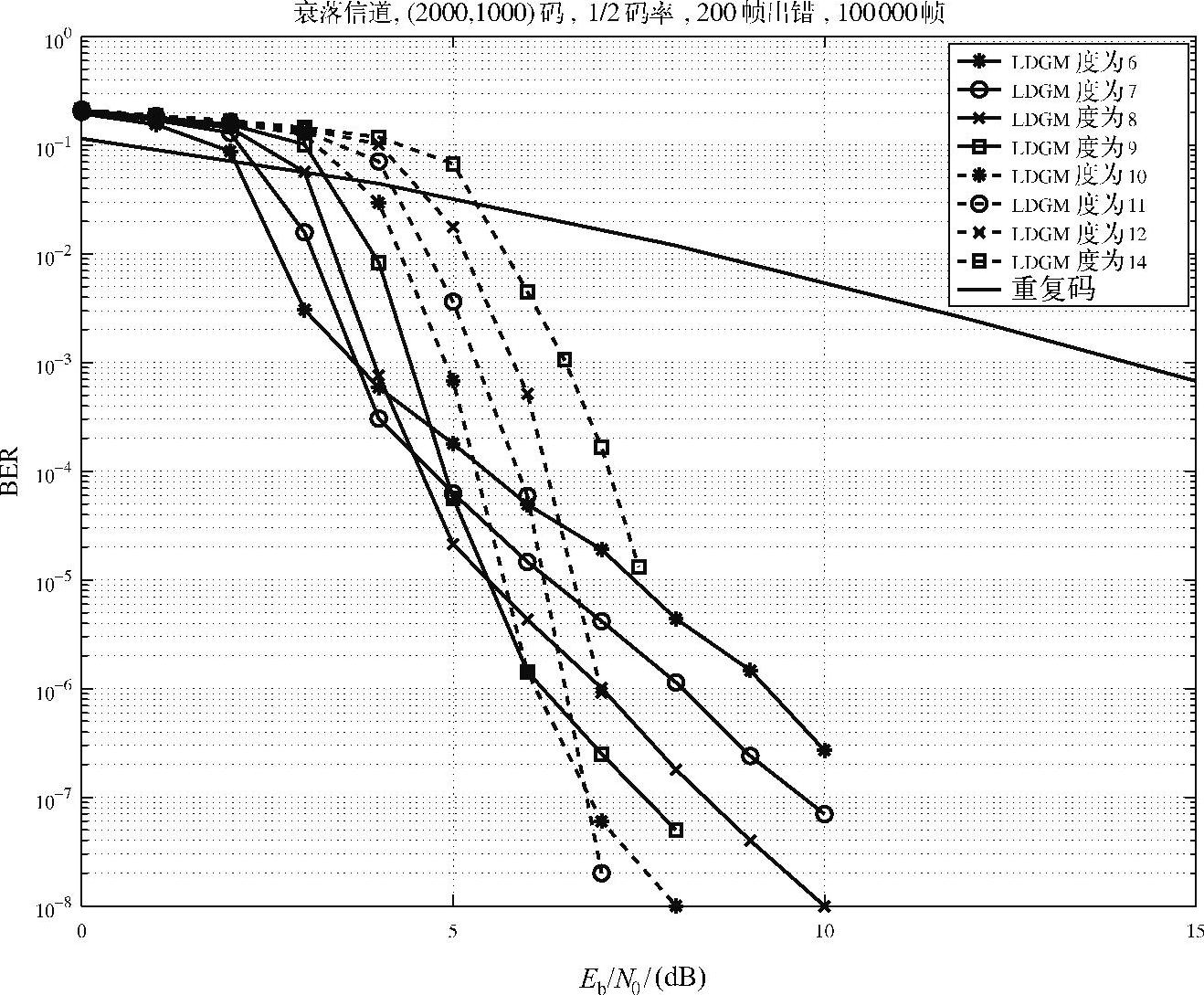
图4.76 瑞利衰落信道下ANCC性能