分布式空时分组码和分布式空时网格码的编码结构决定了它们只能提供有限的编码增益。为了进一步提高系统性能,近年来提出了许多逼近容量的分布式编码方案,例如分布式LDPC码[488,489]、分布式Turbo码(DTC)。实质上这些编码方案是将传统的LDPC码和Turbo码的思想应用于分布式网络。在设计实际的逼近容量的分布式编码方案时遇到的一个挑战是:如何处理中继处产生的译码误差并抑制错误传播。
本节主要考虑分布式Turbo码的设计及其性能分析。分布式Turbo码最早由Zhao和Val-enti[490]提出,之后出现各种改进方案[454,491-494]。本节中我们将介绍两种分布式Turbo编码方案,并分析其性能。
4.3.3.1 Turbo编码结构
Turbo码及其迭代译码的概念最早由Berrou等人于1993年提出[495],它能获得逼近香农限的误码率性能,因而Turbo码也称为逼近容量的可达码。
Turbo码的编码器结构如图4.46所示,它由两个并行的递归系统卷积码(RSC)编码器级联而成,两个RSC编码器通过随机交织器分隔。由于其结构特征,Turbo码也称为并行级联卷积码(PCCC)。编码时,相同的信息序列并行地但以不同的信息比特排列次序进行相互独立的编码,其中第一个编码器直接对输入信息序列进行编码,而第二个编码器则对交织后的信息序列进行编码。两个编码器的输出共同构成Turbo码字。相对于编码器结构,译码器也是由两个级联的分量译码器组成,分隔分量译码器的交织器与编码器中的交织器相同。分量译码器采用基于最大后验概率(MAP)的译码算法,并通过在两个分量译码器之间不断交换并迭代更新软信息实现Turbo译码。Turbo编码的两个必不可少的成员是RSC编码器和随机交织器。RSC码的生成矩阵可表示为

其中,g0(D)和g1(D)分别是反馈多项式和前馈多项式。(n,k)RSC码码字的前k个比特是k个输入信息比特,后n-k个比特是由RSC编码器生成的校验比特。图4.47是一个码率为1/3、分量码为(2,1,3)RSC码的Turbo码编码器的实例,RSC码的生成矩阵为[1, ]
]

图4.46 Turbo码编码器

图4.47 基于[1,5/7]RSC码的Turbo码编码器
4.3.3.2 理想DF下的分布式Turbo码
首先考虑中继能正确译码的理想DF场景。应用Turbo编码原理在无线中继网络构造分布式Turbo码。为简单起见,首先考虑中继始终能正确译码的理想DF场景下的分布式Turbo码设计,然后讨论中继处存在译码错误的实际条件下的分布式Turbo码方案设计。系统模型仍为由单信源、单中继和单目的节点构成的两跳中继系统,我们首先设计其编、译码器结构,然后分析其性能。
1.理想DTC的编码器结构
分布式Turbo编码系统的结构框图如图4.48所示。源节点待发送的二进制比特序列为B=(b1,…bk,…,bL),其中bk为第k个发送信息比特,L为帧长。信息序列B首先送入信道编码器进行编码。为简单起见,考虑码率为1/2的RSC码。码字C表示为
C=(C1,…Ck,…CL) (4.226)
其中,Ck=(bk,ck)是对应于bk的码字,ck∈{0,1}是bk的校验比特。随后码字C被映射为调制符号序列X。为了简化,假设采用BPSK调制方式,调制后的符号序列X为
X=(X1,…,Xk,…,XL) (4.227)
其中,Xk=(xIk,xPk),xIk,xPk∈{-1,1}分别是在时刻2k-1和2k时刻发送的信息位与校验位调制符号。
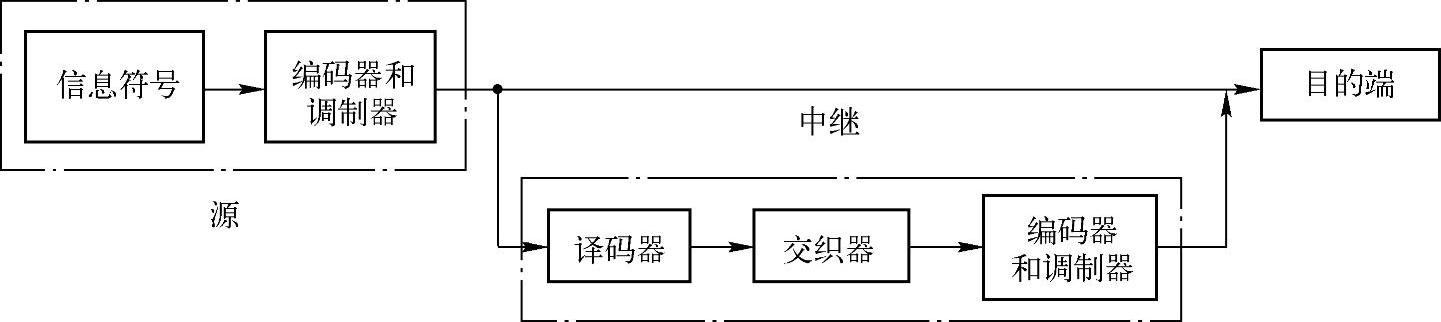
图4.48 理想DTC的系统框图
考虑半双工的传输模式,即源节点和中继在不同的时隙发送数据。在第一个时隙,源节点将信息广播到目的节点和中继。在2k-1和2k时刻中继和目的节点接收到的信号分别为

其中,YSR,k=(yISR,k,yPSR,k);YSD,k=(yISD,k,yPSD,k);pSR=psGSR2与pSD=psGSD2分别是中继和目的节点的接收信号功率,ps是源节点的发射功率,GSR=G0(dSR/d0)-κ/2与GSD=G0(dSD/d0)-κ/2分别是源到中继链路与源到目的节点链路的信道增益,dSR和dSD分别是源与中继以及源与目的节点间的距离,d0是参考距离,G0是一个与载波波长有关的常数,κ是路损因子,一般情况下2≤κ≤6。此外,hSR和hSD分别是源到中继链路及源到目的节点链路的的信道衰落系数,它们可建模为零均值独立复高斯随机变量。本节中考虑准静态衰落信道,即衰落系数在一帧内保持不变但在帧间相互独立的变化。此外,噪声NSR,k=(nISR,k,nPSR,k)与NSD,k=(nISD,k,nPSD,k)都是零均值复高斯随机变量,其每一维的双边功率谱密度为N0/2。不失一般性,假设所有噪声具有相同的方差。事实上当噪声方差不同时可通过适当调整信道增益来实现。
理想DTC时,中继首先对来自源节点的接收信号进行译码、交织。用 表示B经交织后的比特序列。使用与源节点相同的编码器对
表示B经交织后的比特序列。使用与源节点相同的编码器对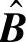 进行编码与调制,得到
进行编码与调制,得到

其中,XR,k=(xIR,k,xPR,k)。在k时刻,中继发送校验符号 ,且满足功率约束条件
,且满足功率约束条件

其中,pR是中继的发送功率约束。对应的目的节点接收到的信号yRD,k为

其中,GRD和hRD分别是中继与目的节点之间链路的信道增益和衰落系数;nRD,k是零均值复高斯分布变量,其双边功率谱密度为N0/2。
目的节点接收的信号由两部分组成,一部分是来自源节点的符号序列YSD=(YISD,YPSD),其中YISD=(yISD,l,…,yISD,L)表示对应于信息位的信号序列,YPSD=(yPSD,l,yPSD,L)是对应于校验位的信号序列;另一部分是中继发送的对应于交织后的乱序信息序列的码字(yRD,l,…,yRD,L)。这两部分信号序列构成了标准的分布式Turbo码。
2.理想DTC的译码器
理想DTC的译码器结构如图4.49所示。与传统的Turbo译码器类似,DTC译码器也由两个级联的分量译码器构成,其中一个对来自源节点的信号序列YSD进行译码,另一个对来自中继的信号序列YRD进行译码。分量译码器采用基于BCJR的MAP译码算法[496]。YISD和YPSD作为第一个MAP译码器的输入,并采用如下方式计算比特序列bk(k=1,…,L)的后验信息(APP)PSD(bk=ω|YSD),ω∈{0,1}:

其中,h是常数以保证∑ωPSD(bk=ω|YSD)=1,且有

其中,m和m′是在卷积码格图中与k时刻输入bk=ω相关联的状态对;Ms是格图中的状态数;αi(m′)和βi(m)分别是前向变量和反向变量,它们可通过下式迭代计算:


图4.49 理想DTC系统的迭代译码器
假设编码结束时编码器对移位寄存器进行复位处理,因此αi(m′)和βi(m)的边界值分别为:α0(0)=1,当m≠0时,α0(m)=0;βl(0)=1,当m≠0时,βl(m)=0。类似地,YRD与 (即YSD的解交织序列)作为第二个MAP译码器的输入。同样可计算交织后信息比特序列
(即YSD的解交织序列)作为第二个MAP译码器的输入。同样可计算交织后信息比特序列 ,k=1,…,L的后验信息,计算方式为
,k=1,…,L的后验信息,计算方式为

其中

图4.49示意了两个译码器之间的Turbo迭代译码过程:第一个MAP译码器计算信息比特序列的后验概率(APP)与外信息,第二个MAP译码器计算交织后的乱序信息比特序列的外信息;第一个译码器输出的外信息经交织后作为第二个译码器的先验信息的更新值。类似地,第二个译码器的外信息在解交织后反馈给第一个译码器,并在下一次迭代时更新其先验信息。经过数次迭代,对第一个译码器输出的APP进行硬判决得到译码结果。
3.性能分析
分析理想DTC的性能时,传统的联合界方法需要计算码字的距离谱,即不同汉明重的码字的个数,这通常需要对卷积码格图进行穷举计算,因此复杂度很高,为此我们转而计算系统的平均上界[497]。
如前所述,DTC的码字是由两部分构成:源节点发送的信息序列对应的码字,以及中继转发的交织后的乱序信息比特流所对应的校验信息。这两组信号在目的节点处具有不同的接收信噪比。两组信号的信噪比γsd和γrd分别为

其中, ,
,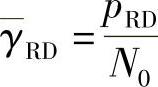 ,而pRD=pRG2RD是目的节点接收到的来自中继的信号功率。令φSD=|hSD|2,φRD=|hRD|2,p(φSD)=e-φSD和p(φRD)=e-φRD分别表示φSD和φRD的概率密度函数(PDF)。现在计算理想DTC的平均错误概率上界。假设发送一个全零码字,译码器错判为汉明重为d的码字的概率,即成对差错概率(PEP)为[491,498]
,而pRD=pRG2RD是目的节点接收到的来自中继的信号功率。令φSD=|hSD|2,φRD=|hRD|2,p(φSD)=e-φSD和p(φRD)=e-φRD分别表示φSD和φRD的概率密度函数(PDF)。现在计算理想DTC的平均错误概率上界。假设发送一个全零码字,译码器错判为汉明重为d的码字的概率,即成对差错概率(PEP)为[491,498]
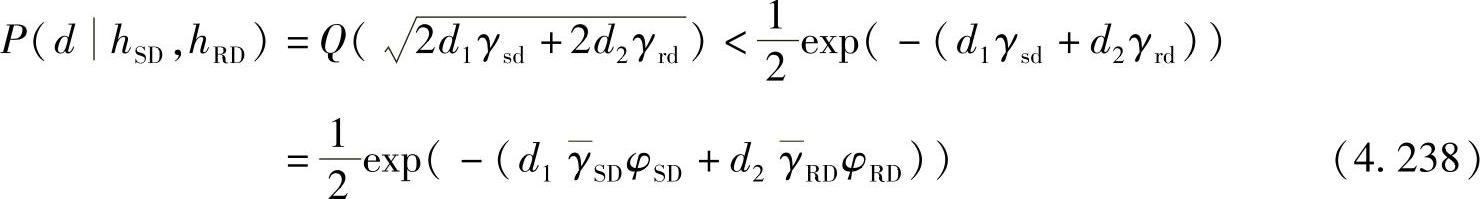
其中,d1和d2是构成码重为d的错误码字中分别来自源节点和中继的部分码字的汉明重,且有d=d1+d2。
对码重为d的错误码字序列进行译码的平均错误概率Pperfect(d)可通过式(4.238)对信道衰落系数φSD和φRD求期望而获得,表示为
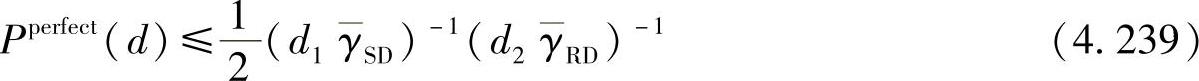
令PPberfect为理想DTC的误码率的平均上界,它可以表示为
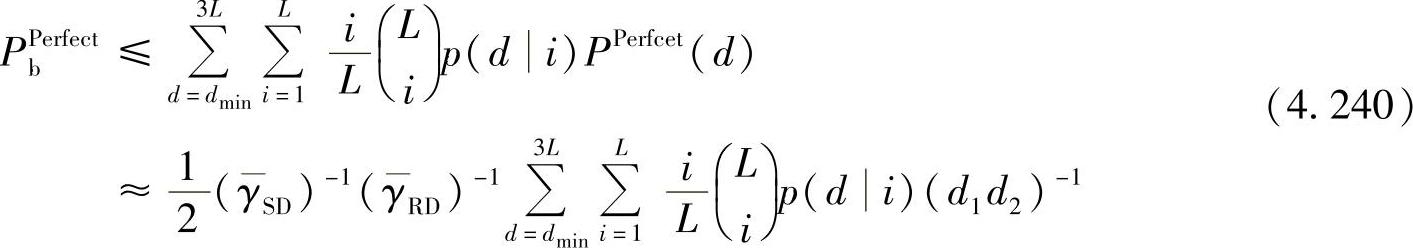
其中,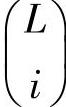 是汉明重为i的码字数量;p(d|i)是输入信息汉明重为i、码字汉明重为d的概率。由式(4.240)可知:理想DTC可获得的分集度为2。需要注意的是,仅在独立快衰落信道下才能获得紧致的联合界[498,499]。为在准平稳衰落信道下获得紧致的上界,可采用在式(4.238)中对衰落系数求期望之前限制其条件上界的方法[498],但这样处理后就无法获得闭式解。在此我们仅将理想DTC作为后面两节中将要介绍的非理想DTC方案的性能下界。由于我们只关注其他DTC方案相对于理想DTC方案的性能损失,因此平均联合界可以有效评估性能。
是汉明重为i的码字数量;p(d|i)是输入信息汉明重为i、码字汉明重为d的概率。由式(4.240)可知:理想DTC可获得的分集度为2。需要注意的是,仅在独立快衰落信道下才能获得紧致的联合界[498,499]。为在准平稳衰落信道下获得紧致的上界,可采用在式(4.238)中对衰落系数求期望之前限制其条件上界的方法[498],但这样处理后就无法获得闭式解。在此我们仅将理想DTC作为后面两节中将要介绍的非理想DTC方案的性能下界。由于我们只关注其他DTC方案相对于理想DTC方案的性能损失,因此平均联合界可以有效评估性能。
4.3.3.3 软信息转发方式的分布式Turbo码
理想的分布式Turbo码方案假设中继能正确译码,而在实际系统中当源节点与中继之间的链路处于深衰落时,中继将发生译码错误。此时如果中继对错误的译码比特进行重编码,则产生错误传播,从而大大降低系统性能。实际系统中,错误传播的危害很大,而且理想译码假设也不符合实际。采用自动重传(ARQ)技术可提高源到中继链路的可靠性,但ARQ会明显降低系统吞吐量。因此,如何解决中继处可能存在的译码错误是分布式Turbo码方案面临的挑战。
在4.2.3节中介绍的软信息转发(SIR)策略可抑制错误传播,本节介绍将SIR应用到DTC中而形成的基于软信息转发的分布式Turbo码(DTC-SIR)。通过后面的分析可知,SIR并不能很直接地应用到DTC之中。在4.2.3节介绍的SIR中,中继译码器计算的是信息符号的软输出,而在DTC中,中继需要计算交织后的信息序列对应的校验序列的软信息,而不是交织前信息序列对应的技验序列的软信息。我们提出一种基于信息符号后验概率进行软编码的方法[454],并可用于DTC-SIR方案,其基本思想是概率推理方法,即中继首先计算信息序列的后验概率,然后推断交织后的乱序信息序列的校验比特序列的后验概率。基于k时刻之前所有符号的概率已知,这种概率推理方法根据卷积码格图结构可计算k时刻交织后的乱序信息比特所对应的校验比特概率,从而可计算校验位符号的软估计值并作为调制符号的概率平均值。
本节将介绍DTC-SIR系统的编码器结构,分析并仿真验证其性能。
1.DTC-SIR编码器结构
DTC-SIR系统的结构框图如图4.50所示。在DTC-SIR中,中继的处理过程可分为两步:译码器首先采用MAP算法计算信息符号序列的后验概率,然后计算交织后的乱序信息符号序列所对应的校验符号的软估计值。

图4.50 DTC-SIR编码器结构
(1)计算信息符号后验概率
接收到来自源节点的信号YSR后,中继计算信息比特的后验概率。令P(bk=ω|YSR),ω∈{0,1}表示信息序列bk,k=1,…,l的后验概率,其计算公式为

其中

(2)计算交织后的乱序信息序列所对应的校验符号软估计值
获得信息符号序列的后验概率P(bk=ω|YSR),k=1,…,l后,中继的软编码器计算交织后的乱序信息序列对应的校验符号序列的软估计值。令

表示信息比特流B交织后的乱序版本,其中 (k=1,…,l)是
(k=1,…,l)是 的第k个符号,
的第k个符号, =bpL表示B的第pk个比特。令
=bpL表示B的第pk个比特。令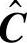 表示
表示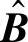 的校验位符号向量,表示为
的校验位符号向量,表示为

其中, 是
是 的校验符号,令
的校验符号,令

表示信息符号的后验概率。令

其中,P( =ω|YSR)=P(bpk=ω|YSR)是第k个乱序信息符号的后验概率,同时也是第pk个信息符号的后验信息。在给定PB或
=ω|YSR)=P(bpk=ω|YSR)是第k个乱序信息符号的后验概率,同时也是第pk个信息符号的后验信息。在给定PB或 的条件下,现计算
的条件下,现计算 的后验概率
的后验概率
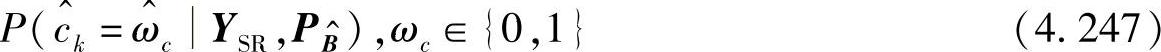
可采用如下所示的递归方法:

其中, 是所有输出校验符号为
是所有输出校验符号为 的分支集合;
的分支集合; 是与校验符号
是与校验符号 相对应的在g(k-1)=m网格状态的信息符号;
相对应的在g(k-1)=m网格状态的信息符号; ,
,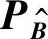 ,g(k-1)=m)表示k时刻信息符号
,g(k-1)=m)表示k时刻信息符号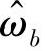 的后验概率,等价于P(bk=
的后验概率,等价于P(bk= YSR);P(g(k-1)=mYSR,
YSR);P(g(k-1)=mYSR, )是k-1时刻状态为m的概率;b(m,m′)表示k时刻导致状态从m′转变为m的输入信息符号,P(b(m,m′)YSR)是信息符号b(m,mn)在k时刻的后验概率。假设编码器在编码结束时对移位寄存器复位处理,从而初始状态概率为
)是k-1时刻状态为m的概率;b(m,m′)表示k时刻导致状态从m′转变为m的输入信息符号,P(b(m,m′)YSR)是信息符号b(m,mn)在k时刻的后验概率。假设编码器在编码结束时对移位寄存器复位处理,从而初始状态概率为
P(g(0)=0)=1,P(g(0)=m,m≠0)=0 (4.250)
(3)实例
为了更好地理解式(4.248)和式(4.249)描述的软编码思想,现在以图4.51所示的格图结构的编码器为例说明软编码。格图中,mi(i=0,1,2,3)表示编码器状态,格图的每个分支上标注的b/bp表示编码器输入比特为b时输出的信息比特为b、校验比特为p。图4.52示意了在计算式(4.248)中 时格图中所涉及的分支,即式(4.248)需对输出的校验比特为0的所有分支求和。在图4.52所示的例子中,
时格图中所涉及的分支,即式(4.248)需对输出的校验比特为0的所有分支求和。在图4.52所示的例子中, 的计算可进一步表示为
的计算可进一步表示为

其中,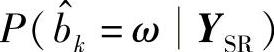 在式(4.246)中给出,并且在计算时最先获得。P(g(k)=m|YSR,
在式(4.246)中给出,并且在计算时最先获得。P(g(k)=m|YSR, )由式(4.249)通过递归计算获得。图4.53示意了
)由式(4.249)通过递归计算获得。图4.53示意了 的计算实例,其中式(4.249)需对转移后状态为m2的所有分支进行求和。此例中,P(g(k)=m2|YSR,
的计算实例,其中式(4.249)需对转移后状态为m2的所有分支进行求和。此例中,P(g(k)=m2|YSR, )可由下式计算获得:
)可由下式计算获得:


图4.51 示例的分量码格图

图4.52 式(4.248)中计算 时的格图
时的格图
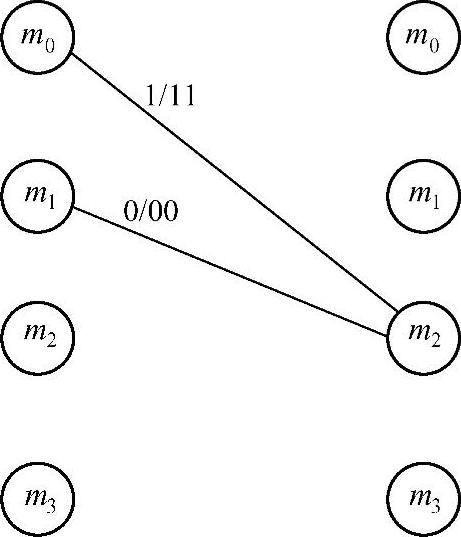
图4.53 式(4.249)中计算 时的格图
时的格图
因此,由B的后验概率,使用式(4.248)和式(4.249)可迭代计算 的后验概率。在式(4.248)~式(4.250)中,只需前向递归计算
的后验概率。在式(4.248)~式(4.250)中,只需前向递归计算 的后验概率。如果同时使用前向和后向递归计算可更精确地计算
的后验概率。如果同时使用前向和后向递归计算可更精确地计算 的后验信息,但计算量也更大。假设采用BPSK调制,二进制比特0和1分别映射为1和-1,校验符号
的后验信息,但计算量也更大。假设采用BPSK调制,二进制比特0和1分别映射为1和-1,校验符号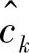 的软估计用xPR,k表示,则有
的软估计用xPR,k表示,则有

参考4.2.3节中的软符号估计(SSE)模型,xPR,k可表示为

其中,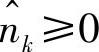 为等效噪声,其期望为(https://www.xing528.com)
为等效噪声,其期望为(https://www.xing528.com)

方差为
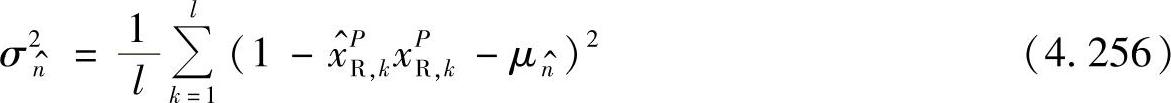
中继发送的信号可以表示为

其中,β是满足中继发送功率约束的归一化因子,可通过下式计算得到

其中pR是中继的最大发送功率约束。令 ,由式(4.258)可得
,由式(4.258)可得

目的节点接收到的对应于中继在k时刻发射的信号为

其中 是目的节点的等效接收噪声,其均值为0,方差为
是目的节点的等效接收噪声,其均值为0,方差为

2.DTC-SIR的迭代译码
分布式Turbo码字由两部分构成:来自源节点的编码信息符号序列以及来自中继的交织后的乱序信息序列所对应的校验符号序列。与理想DTC类似,目的节点的两个译码器基于Turbo原理对此两路信号序列进行迭代译码。为了实现最优的译码,必须获知噪声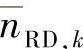 的分布。SIR-SSE方案和DTC-SIR方案的噪声
的分布。SIR-SSE方案和DTC-SIR方案的噪声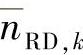 的分布截然不同,这是因为SIR-SSE的中继译码器直接计算信息符号的SSE,而DTC-SIR的中继计算的是交织后的乱序信息序列所对应的校验符号的SSE,而此SSE与源节点编码器所使用的分量码密切相关。当分量码采用非递归卷积码时,DTC-SIR的SSE与SIR-SEE有相似的分布;而当分量码为递归系统卷积码(RSCC)时,两种SEE的分布不同,并且噪声
的分布截然不同,这是因为SIR-SSE的中继译码器直接计算信息符号的SSE,而DTC-SIR的中继计算的是交织后的乱序信息序列所对应的校验符号的SSE,而此SSE与源节点编码器所使用的分量码密切相关。当分量码采用非递归卷积码时,DTC-SIR的SSE与SIR-SEE有相似的分布;而当分量码为递归系统卷积码(RSCC)时,两种SEE的分布不同,并且噪声 的分布非常难以确定。由于Turbo码的分量码通常采用递归系统卷积码,因此噪声
的分布非常难以确定。由于Turbo码的分量码通常采用递归系统卷积码,因此噪声 分布的建模、DTC-SIR的最优译码度量设计就变得非常复杂且颇具挑战性。为使译码器简单易行,仍然假设
分布的建模、DTC-SIR的最优译码度量设计就变得非常复杂且颇具挑战性。为使译码器简单易行,仍然假设 服从近似高斯分布,MAP译码器中与yRD相关联的分支度量γk(m,m′)与式(4.236)稍有不同,将其修正为
服从近似高斯分布,MAP译码器中与yRD相关联的分支度量γk(m,m′)与式(4.236)稍有不同,将其修正为

与SIR-SSE类似,当假设 服从高斯分布时,需修正其方差σ2E。最优的方差σ2E可以通过仿真确定,但这需要大量的仿真运算。为简单起见,在下面的仿真中不对σ2E进行修正,因此如果能更精确地估计σ2E,则可以进一步提升DTC-SIR系统的性能。此外需要指出的是,当实际的噪声
服从高斯分布时,需修正其方差σ2E。最优的方差σ2E可以通过仿真确定,但这需要大量的仿真运算。为简单起见,在下面的仿真中不对σ2E进行修正,因此如果能更精确地估计σ2E,则可以进一步提升DTC-SIR系统的性能。此外需要指出的是,当实际的噪声 不服从高斯分布时,式(4.262)所示的译码度量将不再是最优的。因此,如果噪声
不服从高斯分布时,式(4.262)所示的译码度量将不再是最优的。因此,如果噪声 的分布能够准确建模并相应设计译码器,则可以进一步提升DTC-SIR的性能。如何实现最优的DTC-SIR仍是一个有待解决的问题。
的分布能够准确建模并相应设计译码器,则可以进一步提升DTC-SIR的性能。如何实现最优的DTC-SIR仍是一个有待解决的问题。
3.性能评估
本节中将仿真对比不同的DTC方案的性能。仿真中采用BPSK调制,帧长为130个符号,经历准平稳衰落信道。为简单起见,假设 等于
等于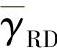 。采用4状态、码率为1/2的RSC码作为Turbo码的分量码,RSC码的生成矩阵为(1,5/7),其自由距离为5。在如下两种仿真条件下对比各DTC方案性能:
。采用4状态、码率为1/2的RSC码作为Turbo码的分量码,RSC码的生成矩阵为(1,5/7),其自由距离为5。在如下两种仿真条件下对比各DTC方案性能:
(1) 不相同时
不相同时
仿真系统设置为:源到中继的信号功率固定,而源到目的节点以及中继到目的节点的两路信号的功率发生变化。
对于传统的没使用ARQ技术的DTC而言,无论中继能否正确译码,中继始终转发重编码信息。因此,当中继发生译码错误时,中继对错误的译码序列进行重编码将造成错误扩散。将这种DTC方案称为无ARQ的DTC。仿真中,采用Log-MAP译码算法。在DTC-SIR方案中,与目的节点的噪声方差相对应的等效噪声方差可由式(4.255)计算获得,与软估计的误差方差相对应的等效噪声方差可由式(4.256)计算获得。无ARQ的DTD方案并无任何中继是否正确译码的信息,因此译码时仅考虑接收噪声方差,这将进一步降低系统的性能。
正如之前所讨论的,在源到中继链路上使用ARQ技术将大大提高DTC的性能,这种能逼近理想DTC性能的方案在此称为DTC-ARQ方案。在下面的DTC-ARQ仿真中,假设最大重传次数为3,如果3次重传后仍译码失败则认为发送失败,此时中继不再转发此失败帧而将其抛弃。
图4.54~图4.56给出了无ARQ的DTC、有ARQ的DTC以及DTC-SIR三种方案在γ 固定时误码率(BER)随
固定时误码率(BER)随 变化的仿真结果。从仿真结果可见,由于错误传播,无ARQ的DTC方案性能非常差,即使
变化的仿真结果。从仿真结果可见,由于错误传播,无ARQ的DTC方案性能非常差,即使 较高其误码率性能也很快出现错误平层,这种趋势在
较高其误码率性能也很快出现错误平层,这种趋势在 较低时尤为明显。DTC-SIR方案可以有效地抑制错误传播,因而其性能随着
较低时尤为明显。DTC-SIR方案可以有效地抑制错误传播,因而其性能随着 增加而逐渐逼近有ARQ的DTC方案。
增加而逐渐逼近有ARQ的DTC方案。

图4.54  时的BER性能比较
时的BER性能比较

图4.55  时的BER性能比较
时的BER性能比较
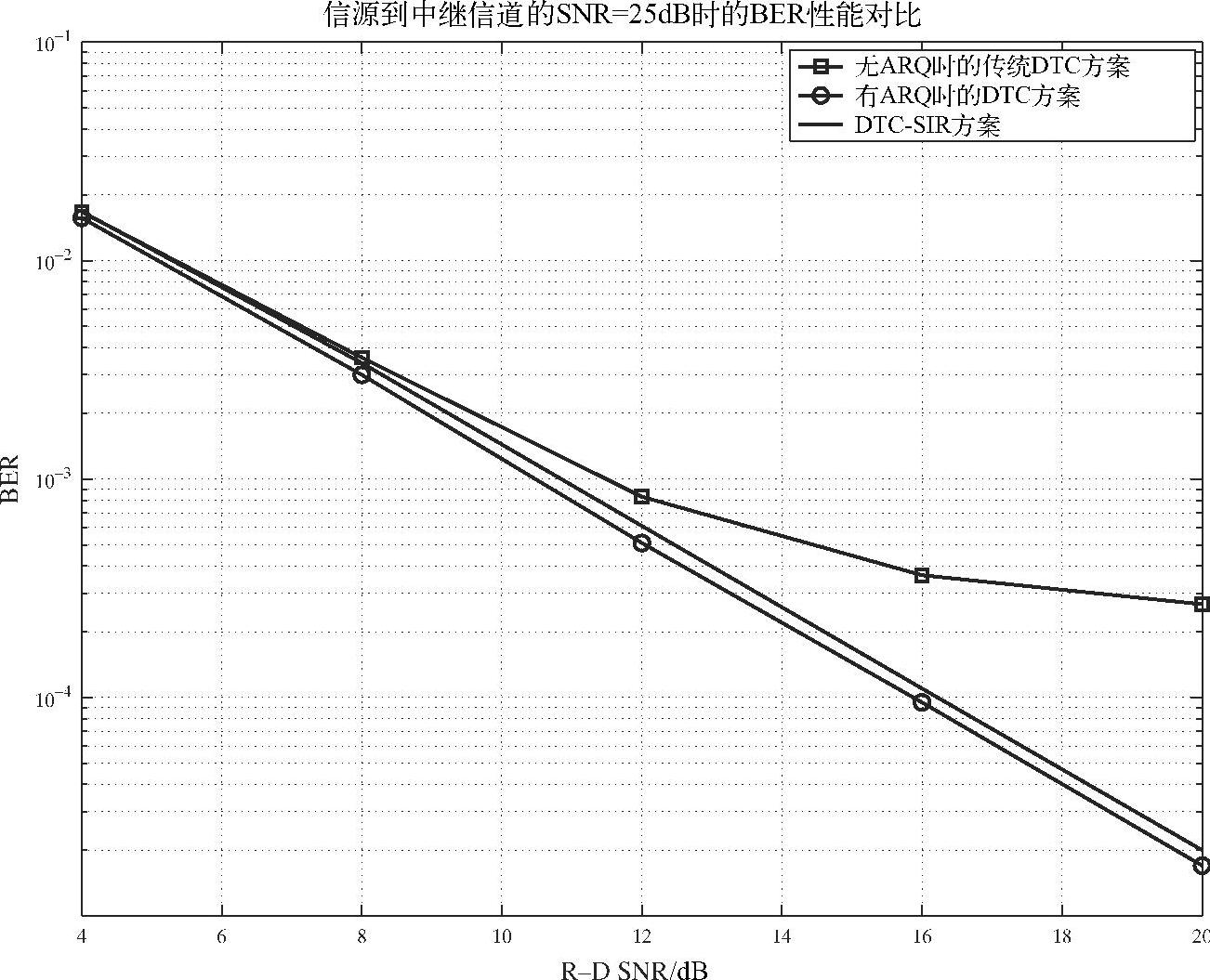
图4.56  时的BER性能比较
时的BER性能比较
(2)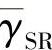 与
与 间SNR的差距不同时
间SNR的差距不同时
仿真条件为:源至中继链路与中继至目的节点链路具有不同的信噪比差。假设信号能量随传输距离的增加以指数形式衰减,很显然,SNRGap由源节点与中继的发送功率之比以及相对距离dSR、dRD决定,具体有

其中,pS是源节点的发送功率;pS/pR和(dSR/dRD)-κ分别对应于功率放大因子和几何分布因子,可分别表示为ρPsr和ρsrd;ρsrP表示源节点与中继的发射功率之比,ρsrd表示dSR与dRD的比值,它与系统的几何分布(中继与源节点以及目的节点的相对位置)有关。通过评估不同的SNR差距下DTC-SIR的性能,可分析功率放大因子和几何分布对系统性能及吞吐量的影响。
图4.57和图4.58给出了不同的SNR差距对BER性能的影响。由仿真结果可见,DTC-SIR远优于无ARQ的DTC方案,且随着SNRGap的增加逐渐逼近DTC-ARQ方案的性能。例如,考虑BER为10-4,在SNRGap分别为0dB和4dB时,DTC-SIR与DTC-ARQ的性能差距大约为1.5dB和0.5dB。当SNRGap更大时,DTC-SIR的性能将更逼近DTC-ARQ方案。
如式(4.263)所示,SNRGap决定于功率放大因子ρsrP和几何分布因子ρsrd,因而增大ρsrP和ρsrd即增加SNRGap可提高DTC-SIR的性能,这意味着可通过系统配置使中继位置更靠近源节点和/或使源节点发送功率大于中继发送功率来实现DTC-SIR性能的提升。

图4.57 SNRGap=0 dB时的BER性能比较

图4.58 SNRGap=4dB时的BER性能比较
4.3.3.4 广义分布式Turbo码
在上节中,我们介绍了一种实际衰落信道下中继存在译码错误时的实用分布式编码方案,该方案主要针对单中继系统。本节将针对具有多个中继的两跳中继网络,提出一种广义分布式Turbo码方案(GDTC)。在GDTC方案中,根据中继能否正确译码,将中继分为两组,一是DF中继组:能成功译码的中继组,采用DF转发策略;二是AF中继组:不能成功译码的中继组,采用AF方式。这种转发策略非常类似于4.2.4节的操作:AF中继组的所有中继放大并转发接收信号,DF中继组的所有中继对接收信号进行译码、交织、重编码并转发。在目的节点处,所有来自AF中继组的信号被合并为GDTC码字的一个信号,而所有来自DF转发组的信号被合并为另一个信号。最终,两路合并信号构成广义DTC码。
类似于ARP,实际系统中通常在信息块(帧)上增加CRC校验,中继在每帧数据译码后通过CRC校验来判定译码是否正确。为了降低复杂度,中继仅将每帧数据的接收SNR与一个由码的Bhattacharyya参数所确定的阈值相比较来判定是否正确译码。也就是说,中继仅对接收SNR高于阈值的帧进行译码,其余数据帧假设不能正确译码,从而不进行译码处理。
本节介绍GDTC的编码器结构,分析并仿真评估其性能。
1.GDTC编码器结构
考虑由一个源节点、n个中继和一个目的节点构成的两跳中继网络。假设源与目的端间存在直传链路,并延用前几节的定义。设信道编码采用码率为1/2的RSCC,调制方式为BPSK,且所有中继的发射功率同为pR。图4.59是GDTC方案的框图。

图4.59 GDTC方案的框图
源节点的信息比特序列为B=(b1,…,bk,…,bL),其中L为序列长度。B经信道编码后调制为X=(X1,…,Xk,…,XL),其中Xk=(xkI,xkP),xkI,xPk∈{-1,1}分别是在2k-1和2k时刻发送的调制后的信息符号和校验符号。目的节点和中继能同时接收Xk,中继i和目的节点的接收信号分别为

其中,piSR=ps·(GiSR)2与pSD=ps·(GSD)2分别是在中继i和目的节点的接收信号功率;ps是源节点的发送功率;GiSR和GSD分别是源到中继i以及源到目的节点的信道增益;hiSR和hSD分别是源到中继i以及源到目的节点的信道衰落系数;NiSR,k和NSD,k是噪声矢量,其每一分量都是零均值、双边功率谱密度为N0/2的复高斯随机变量。
与4.2.4节介绍的ARP方案相似,在每次数据帧的发送中,GDTC方案根据中继是否可以正确译码,将所有中继分成AF中继组ΩAF和DF中继组ΩDF。
AF中继组中的每个中继放大并转发接收信号。在目的节点处,所有来自AF中继组的信号合并为一个信号

其中,YRD-AF,k是目的节点对来自于AF中继组的接收信号进行合并后的信号,WSD和WiR,i∈ΩAF是合并系数。目的节点处的合并信号的SNR用γAF表示,可近似计算为

其中, ,
, ,γ
,γ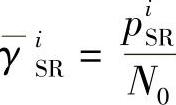 ,
, 是变量λi,p,p=1,2的调和平均值,其中
是变量λi,p,p=1,2的调和平均值,其中 。DF中继组中的每个中继先对接收信号进行译码以恢复原始信息比特序列B,然后经交织得到
。DF中继组中的每个中继先对接收信号进行译码以恢复原始信息比特序列B,然后经交织得到 ,再通过重新编码与调制后得到发送符号序列XR
,再通过重新编码与调制后得到发送符号序列XR
XR=(XR,1,…,XR,k,…,XR,L) (4.267)
其中,XR,k=(xIR,k,xPR,k)是对应于 的调制码字;xIR,k和xPR,k是相应的信息调制符号与校验调制符号。DF中继组的第i个中继以发送功率piR转发调制符号XR,k,目的端相应的接收信号为
的调制码字;xIR,k和xPR,k是相应的信息调制符号与校验调制符号。DF中继组的第i个中继以发送功率piR转发调制符号XR,k,目的端相应的接收信号为

在目的端,所有来自DF中继组的信号被合并在一起,合并信号YRD-DF,k为

来自DF中继组的合并信号在目的端的SNR为

2.GDTC的迭代译码
由式(4.265)和式(4.269)可见,广义分布式Turbo码的码字由来自AF中继组的编码信息序列和来自DF中继组的编码交织信息符号序列构成,这两组信号序列分别表示为YRD-AF和YRD-DF。令YIRD-AF、YIRD-DF、YPRD-AF、YPRD-DF分别表示YRD-AF和YRD-DF中相应的信息符号序列及校验符号序列。其中YIRD-AF和YIRD-DF携带相同的信息,因此在译码前先需合并。
用I(a)和I-1(a)分别表示序列a的交织版本和解交织版本,用YIAF表示合并的信息符号序列,而用YIDF表示其交织版本,则有

进一步令YAF=(YIAF,YPRD-AF),YDF=(YIDF,YPRD-DF)。YRD-AF和YRD-DF分别送入两个卷积码译码器,并在这两个译码器之间进行Turbo迭代译码。与传统Turbo迭代译码过程相同,两个MAP译码器分别计算输入符号YAF和YDF的后验概率信息(APP)与外信息,一个译码器输出的外信息经交织或解交织后作为另一个译码器的先验信息。经过多次迭代,第一个译码器输出的后验概率信息进行硬判决并输出。GDTC译码流程如图4.60所示。

图4.60 GDTC迭代译码框图
存在这样一种可能:某些数据帧由于经历深衰落从而没有任何中继可以正确译码,即不存在DF中继组。此时仅对YRD-AF进行译码,以获得信息符号的估计值。
3.性能分析
本节分析GDTC的性能。不失一般性,假设GiSR=GSR,i=1,…,n,从而有piSR=pSR,i=1,…,n。与4.2.4节中分析ARP类似,首先计算编号为1~q的q个中继组成的AF中继组和编号为q+1~n的n-q个中继组成DF中继组的成对差错概率。与式(4.117)~式(4.119)的分析过程一致,高信噪比时GDTC的成对差错概率可以表示为

其中,d1和d2分别是汉明重为d的错误码字中来自AF中继组和DF中继组的错误部分的汉明重,且有d=d1+d2;γAF,(q)和γDF,(n-q)分别表示来自AF中继组和DF中继组的合并信号的瞬时接收信噪比,分别为

 表示源到中继i信道下的条件码字错误概率,它由式(4.118)给出。遵循4.2.4节的分析,高信噪比时的平均成对差错概率PGDTC(d)可由下式得到:
表示源到中继i信道下的条件码字错误概率,它由式(4.118)给出。遵循4.2.4节的分析,高信噪比时的平均成对差错概率PGDTC(d)可由下式得到:

令PbGDTC表示GDTC方案的误码率上界,高信噪比时该上界可以近似为

其中, ,p(d|i)表示输入汉明重为i、输出码字汉明重为d的概率。从式(4.273)可见,随着
,p(d|i)表示输入汉明重为i、输出码字汉明重为d的概率。从式(4.273)可见,随着 ,由n个中继构成的中继网络的GDTC方案可以获得的分集度为n+1。同样,对于理想DTC,由于所有中继都能正确译码,码重为d的码字的错误译码的平均成对差错概率
,由n个中继构成的中继网络的GDTC方案可以获得的分集度为n+1。同样,对于理想DTC,由于所有中继都能正确译码,码重为d的码字的错误译码的平均成对差错概率 为
为

高信噪比下,理想DTC的平均误码率上界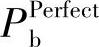 可近似为
可近似为

式(4.274)可以进一步表示为
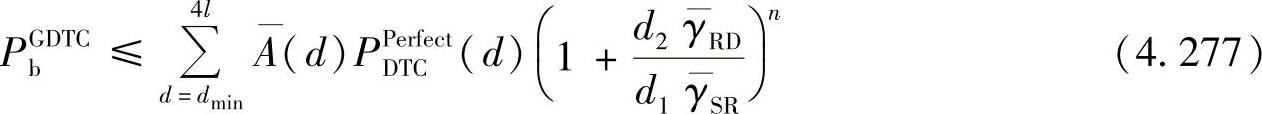
对于式(4.277),需要指出的是当 时,PbGDTC→PbPerfect,GDTC的性能逼近理想DTC方案,这与DTC-SIR的性能趋势相同。
时,PbGDTC→PbPerfect,GDTC的性能逼近理想DTC方案,这与DTC-SIR的性能趋势相同。
4.性能评估
本节给出GDTC方案的仿真结果。所有仿真都基于BPSK调制方式,且数据帧包含130个符号,信号经历准平稳衰落信道。编码采用4状态RSC码,码率为1/2,生成矩阵为(1,5/7)。假设对于所有的i=1,…,n,γsr,i=γsr,γrd,i=γrd,并且γrd=γsd。
图4.61~图4.64给出了不同中继数下GDTC、AF转发方式的分布式编码(DC-AF)以及理想分布式Turbo码的性能对比结果。在仿真结果图中,‘S-R SNR’表示源到中继信道的信噪比 ,‘R-D SNR’表示中继到目的端信道的信噪比
,‘R-D SNR’表示中继到目的端信道的信噪比 。由仿真结果可见,随着中继数目的增加,GDTC方案在所有SNR条件下都远优于DC-AF方案,且随着
。由仿真结果可见,随着中继数目的增加,GDTC方案在所有SNR条件下都远优于DC-AF方案,且随着 的增加,其性能逐渐逼近理想DTC方案,此仿真结果与理论分析结论一致。
的增加,其性能逐渐逼近理想DTC方案,此仿真结果与理论分析结论一致。

图4.61 单中继时的FER性能

图4.62 双中继时的FER性能

图4.63 4中继时的FER性能

图4.64 8中继时的FER性能
从上面的仿真结果可见,在低 和高
和高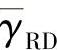 条件下GDTC方案和DC-AF方案表现出相似的性能。然而随着J的增加,例如n=4或8时,GDTC方案的性能远优于DC-AF方案。此趋势很容易解释:对于低
条件下GDTC方案和DC-AF方案表现出相似的性能。然而随着J的增加,例如n=4或8时,GDTC方案的性能远优于DC-AF方案。此趋势很容易解释:对于低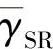 ,源到中继信道噪声水平高,中继出现错误译码的概率较高,因此大多数中继不能正确译码,如果中继数n较小时,那么大多数中继都将以AF方式转发信息,而DF中继组中的中继数很少。然而即使是DF中继组的中继数目很少,在中继到目的端信道SNR很低时依然能带来显著的编码增益,因为此时DF中继组即使少量的中继也能显著提升中继信道的质量。随着中继数目的增加,DF中继组包含至少一个中继的概率也随之增加,从而DF中继组带来的编码增益更加明显。这就解释了即使γSR很低时随着中继数的增加,GDTC方案比DC-AF方案能提供显著的编码增益的原因。
,源到中继信道噪声水平高,中继出现错误译码的概率较高,因此大多数中继不能正确译码,如果中继数n较小时,那么大多数中继都将以AF方式转发信息,而DF中继组中的中继数很少。然而即使是DF中继组的中继数目很少,在中继到目的端信道SNR很低时依然能带来显著的编码增益,因为此时DF中继组即使少量的中继也能显著提升中继信道的质量。随着中继数目的增加,DF中继组包含至少一个中继的概率也随之增加,从而DF中继组带来的编码增益更加明显。这就解释了即使γSR很低时随着中继数的增加,GDTC方案比DC-AF方案能提供显著的编码增益的原因。
仿真结果进一步验证了GDTC在所有SNR范围内都能获得显著的编码增益,并随着γSR的增加更逼近理想DTC的性能。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




