分布式空时分组码的应用技术

沿用文献[51，467]中总结的方法，分布式空时分组码设计的目的是针对采用估计转发方案的分布式多跳网络，设计分数资源分配方案。在此主要针对每个转发阶段的分数帧时隙分配、功率分配与调制阶数设计，从而获得最大的端到端吞吐量。

本节首先给出系统模型，然后推导分布式空时分组码的错误概率，并基于此性能分析设计资源分配策略，从而使对于在同一转发时隙内的节点，无论其拓扑结构是完全协同还是部分协同，都能获得最大的端到端吞吐量。

4.3.1.1 系统模型

考虑图4.26示意的拓扑结构，即源节点经由若干中继与目的节点通信。此种拓扑结构中存在一个或多个相互干扰的信息流，表征了多跳分布式空时拓扑结构。空间上相邻的多个中继构成中继虚拟天线阵列（VAA）。我们将传输过程简单地划分为发送、转发和接收VAA三个阶段。

构成分布式MIMO多阶段中继网络的收发器功能模块如图4.27所示，其上层表示相应于源节点的源虚拟天线阵列（S-VAA），中层是相应于中继节点的中继虚拟天线阵列（R-VAA），下层是相应于目的节点的目的虚拟天线阵列（D-VAA）。图中每一层虚拟天线阵列都含有三个节点终端，这只是为了方便理解，实际上虚拟天线阵列可以含有任意合理数目的节点终端。下面详细介绍系统模型的核心模块。

●S-VAA。信源将信息传送给协同收发器，协同收发器将信息转发给同一VAA中空间相邻的中继节点。与本书中提到的其他方案不同，S-VAA的通信通过空中接口完成，这种空中接口与不同阶段之间进行通信的空中接口或者不需要任何优化处理的空中接口完全不同，且这种通信方式之后不再进一步考虑。假设空间相邻的协同节点的通信距离较短，因此可假设这些协同通信链路是无差错的。S-VAA中的每一个终端按照预先设定的码本进行分布式空时分组码的编码操作，然后空间上分离的节点经同步后把编码信息发送出去。同步不是本节讨论的问题，感兴趣的读者可以参见文献[388，468-479]。

●R-VAA。VAA中每个中继接收数据后选择性地对这些接收数据进行解码，然后传送给协同收发器。理论上，每个终端与其他所有终端都进行协同，实际上任意的协同度都可行。如果中继终端不进行解码，则它与其他中继交换的是未经处理的或采样后的接收信号，此时等效于透明中继过程。协同处理并适当解码后，重构的信息再经分布式重编码、同步并转发至随后的R-VAA层。

●D-VAA。D-VAA的功能模块的过程与S-VAA相反，即所有终端接收信息后首先解码然后传送给协同收发器，协同收发器再将数据转发给目标终端。数据经过处理后最终传递给信宿。

下面详细描述分布式编解码器的功能模块，其结构如图4.28所示。

●分布式编码器。分布式编码器中的信道编码器与非分布式的编码器相同，但是通常需要针对分布式特征来设计信道编码方案。空时编码器通过使阵元相隔足够远而获得额外的空间维资源（空间分集）来提高系统性能。分布式空时码与传统的空时码不同，因为构成完整码字中多个部分是从空间上相隔离的多个终端传送的，所有终端上传输的部分码字构成一个完整的空时码字。因此，每个分布式空时编码器都需要由控制信号来指示发送构成完整空时码字的哪个部分，即如图4.28所示的控制信号#2。在此假设空时编码器已知这个控制信息。

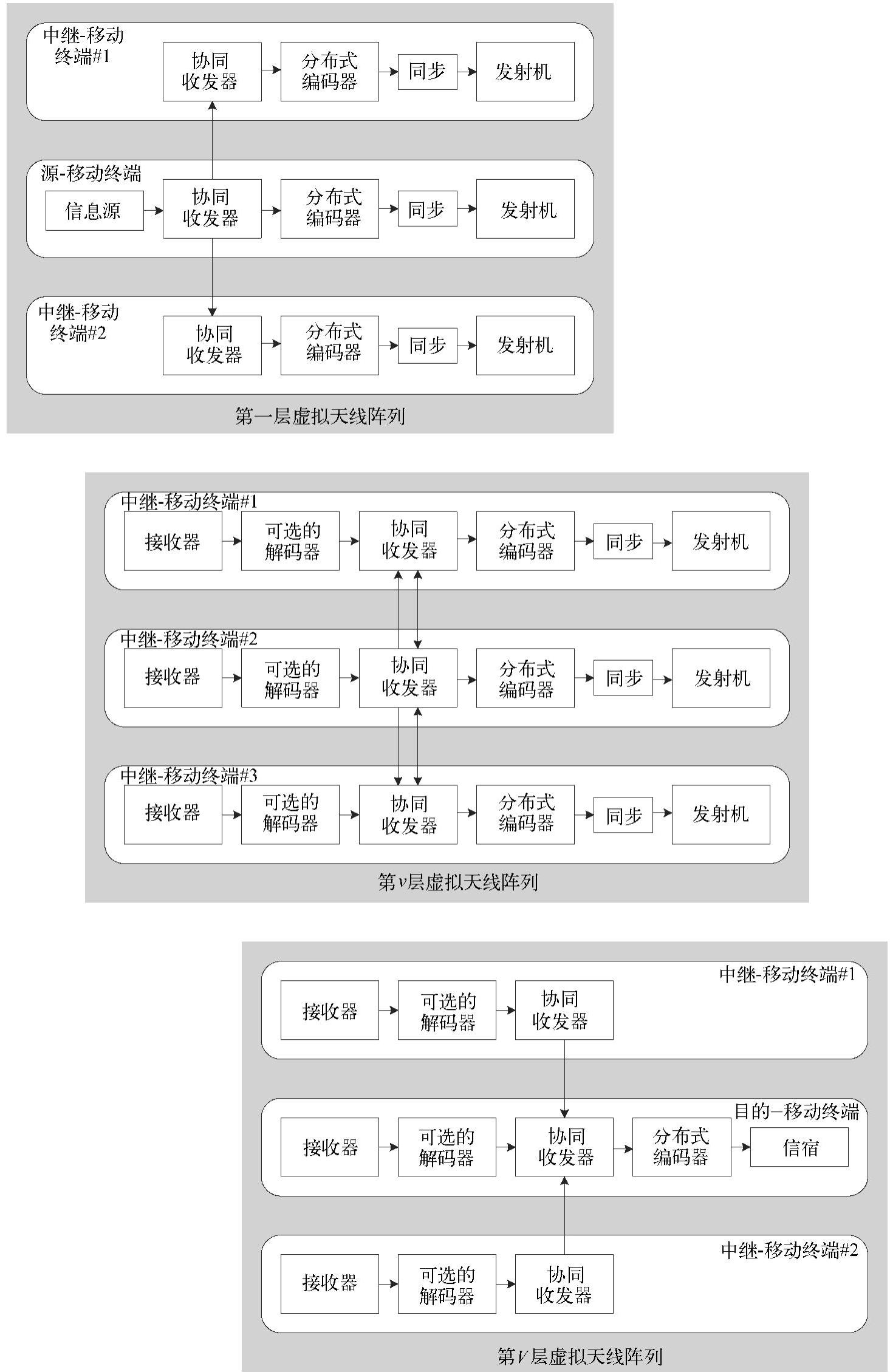
图4.27 S-VAA（上）、第v个R-VAA（中）与D-VAA（下）的功能模块

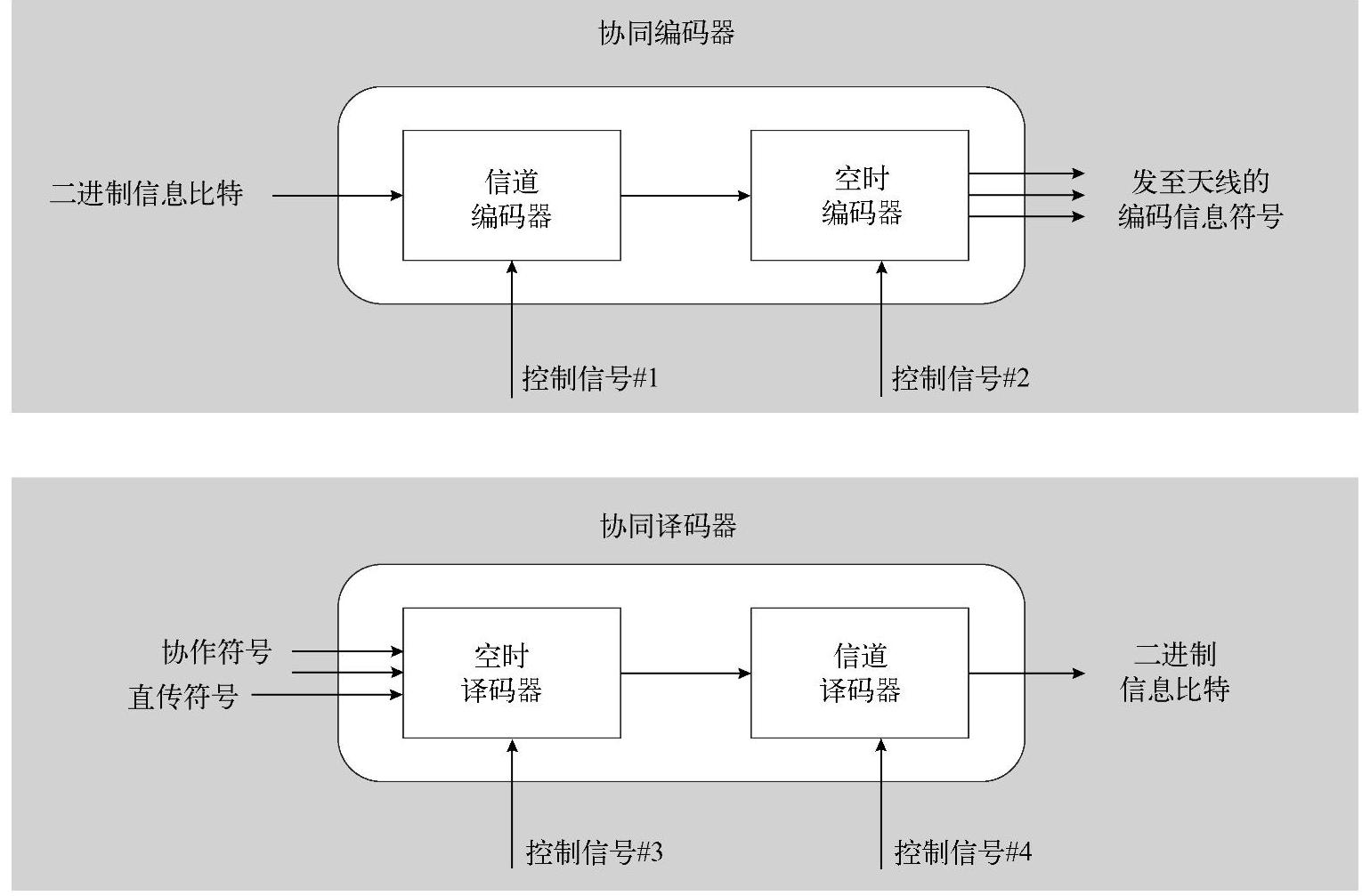
图4.28 分布式编解码器

●分布式解码器。协同解码器可以看做是协同发送器的逆过程。空时解码器的输入由两部分组成：直传链路传输的信号，以及由相邻节点经协同链路传输的信号。为了实现最佳解码，需要由控制信号说明输入空时解码器的信息类型。例如，控制信号可以是一位比特信息，用来通知解码器来自相应的协同中继的采样软信息信号是否可获得。经过空时解码，信息被传送到信道解码器进行信道译码。在协同解码器中，最终得到的二进信息输出可能输入到协同编码器，从而转发至下一个VAA层。

在下面的分析中，假设中继接入方案采用时分多址接入（TDMA），因此所有中继链路都使用整个频带带宽W，但是每个中继阶段只占用帧长T的部分时隙来转发信息。我们首先分析分布式空时分组码的错误概率，然后基于分析结果求取近似最优的资源分配策略。

4.3.1.2 分布式空时分组码的错误概率

图4.28示意了由传统STBC实现的空时编码器，它并没有根据分布式的拓扑结构而改变，很显然它是次优的方案，但它有助于理解分布式空时编码。如果获得了分布式空时分组码的错误概率表示，则使用同样的分析方法可以获得合适的资源分配策略。

图4.29示意了一个典型的具有t根发送天线和r根接收天线的空时编码MIMO系统。假设有b·s个信息比特输入调制器，经格雷映射将b=log₂M个连续比特根据M-PSK或M-QAM的星座图映射为s个调制符号x₁，x₂，…，x_s。这些符号随后根据d×t维的正交空时编码矩阵G进行空时编码，其中d是传送空时码字所需要的符号数目，t是发送天线阵元的数目。在k时刻（k=1，…，d），经空时编码后的符号c_k，i∈G从第i（i=1，…，t）根发送天线发送出去，因而传输速率可减为R=s/d。空时码生成矩阵G将符号x₁，x₂，…，x_s映射为t×d维的空时矩阵X，即

空时码字经由r×t维的平坦衰落空时信道传输，此信道可以用第2章介绍的矩阵H表示，则接收信号的矩阵表示形式为^[480]：

Y=HX+N （4.130）

其中，N是r×d维接收噪声矩阵，其协方差矩阵为

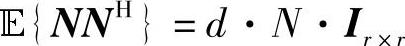
其中，N是在空间和时间上每个采样的总噪声功率。假设接收端可以获得完整的信道状态信息，已知Y检测X的问题等价于在所有可能的符号x₁，x₂，…，x_s上最小化ML判决度量‖Y-HX‖^[121，480]，因此检测复杂度随着天线总数r×t线性增加，随着调制阶数M和码字长度d而呈指数增加。在文献[480]中已证明了若空时码生成矩阵G具有正交性，则可将ML问题转化为s个并行的、单独针对每个发送符号x_l∈（1，s）的ML判决问题。Larsson和Stoica在文献[480，102页]中给出了最优的判决度量，此时检测复杂度只随着调制阶数M指数增加，从而极大地简化了检测过程。

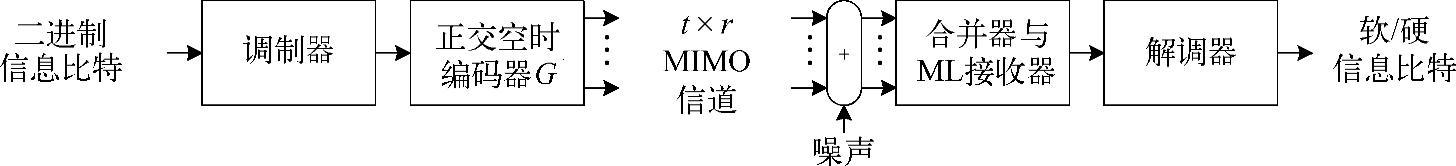
图4.29 空时块编码MIMO系统（O-MIMO）

利用Larsson和Stoica定理7.3[480]，可得到检测端每个符号x_l∈（1，s）的瞬时SNR为

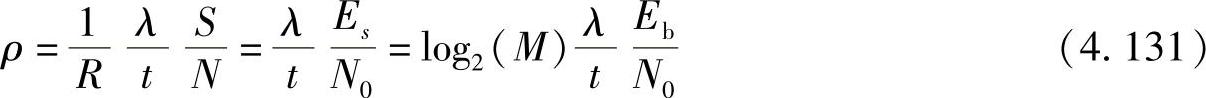
其中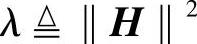，；S是信号的平均发送功率；E_s是每符号的平均发送能量；E_b是每比特的平均能量；N是平均接收功率；N₀是接收噪声的平均功率谱密度。由此可得到矩生成函数（MGF）为

基于Hasna和Alouini^[271]以及Shin和Lee^[481]给出的结论，可以得到M-PSK和M-QAM方案的误符号率（SER）的闭式解。Hasna和Alouini的文献[271]指出，相干M-PSK的平均SER为

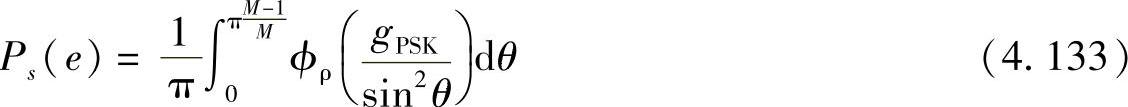
其中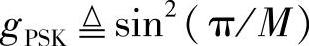，。由式（4.132），上式又可以写为

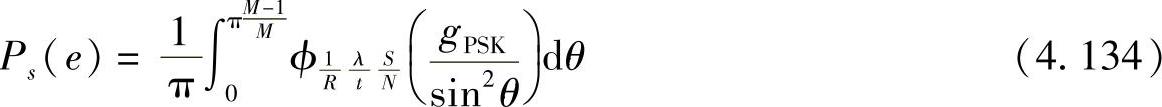
类似地，可得到相干M-QAM的SER为[271]

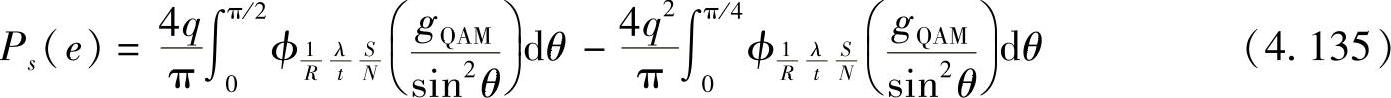
其中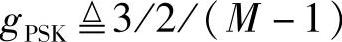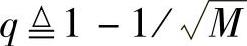，；。由此我们可以推导出不同正交空时分组码方案的误符号率闭式解。

（1）瑞利衰落——子信道增益相等

当子信道的增益都相同时，即γ₁=…=γ_u≜γ，瞬时SNR的MGF为

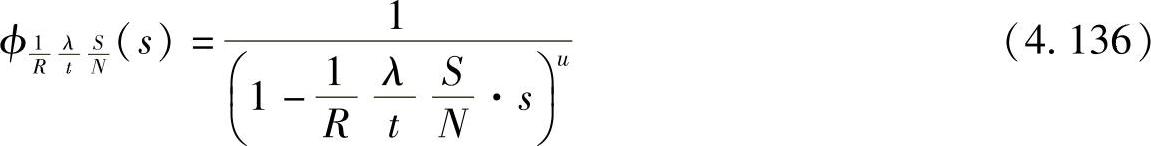
其中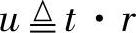，。M-PSK的SER的闭式解为

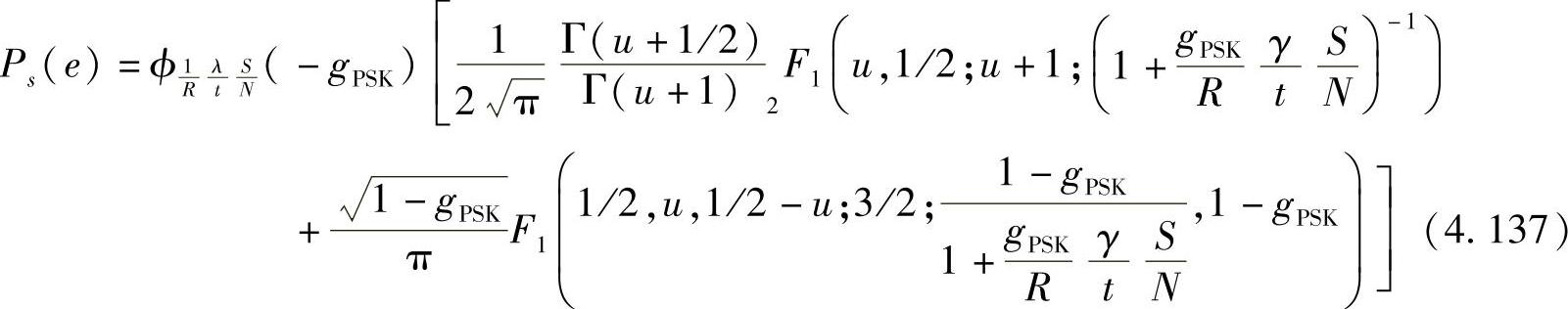
其中，2F₁是含有两个参数的一般超几何函数（9.14.1节）^[268]，也称为高斯超几何函数（9.14.2节）^[268]，其中两个参数分别为类型1参数和类型2参数；F₁是包含两个变量的超几何函数（9.180.1节）^[268]，也称为Appell超几何函数。为简化随后的分析，式（4.137）可表示为P_PSK（u，t，R，γ，S/N，M）。类似地，M-QAM的SER为^[467，481]：

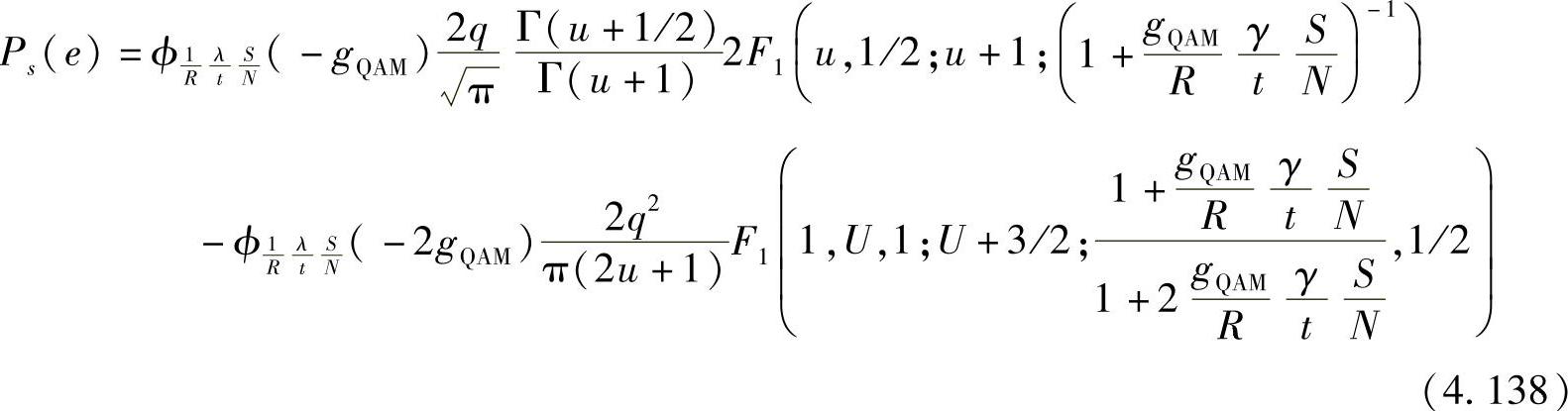
同样为简洁起见，式（4.138）可表示为P_QAM（u，t，R，γ，S/N，M）。

（2）瑞利衰落——子信道增益不相等MGF为[467]

其中，常数K_i为

其中，γ_i为第i径的平均信道增益。由此可得分布式STBC的SER的闭式解（所有的信道增益各不相同）。采用简化的表示方法，错误概率可表示为^[467]

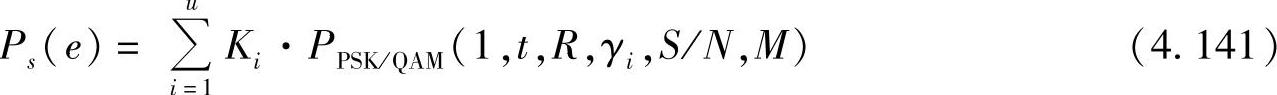
（3）瑞利衰落——子信道增益一般的情形

此时有g≤u个不同的子信道增益，相应的SNR表示为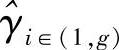，每个SNR重复v_{i∈（1，g）}次，因此MGF为

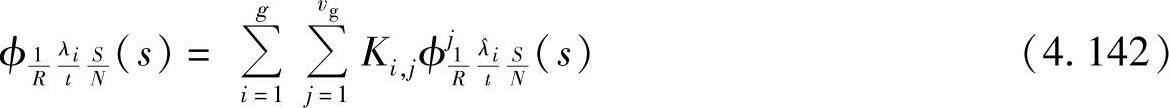
其中，系数K_i，j为^[467]：

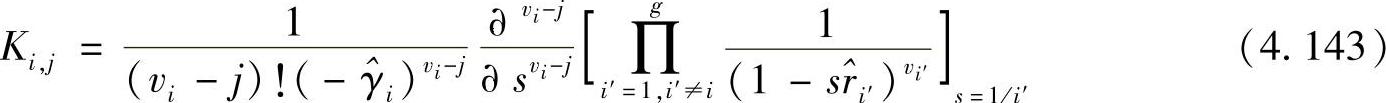
则错误概率可以表示为

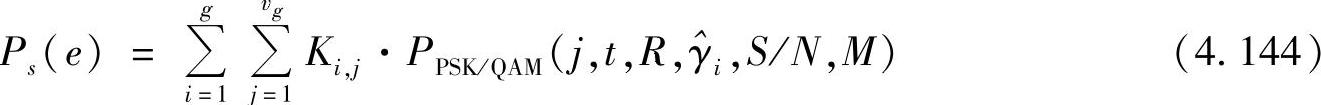
（4）Nakagami衰落——子信道增益相等

若已知Nakagami衰落因子m，则类似于以上分析，可得错误概率为

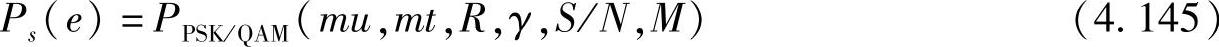
（5）Nakagami衰落——子信道增益不相等

对于有不同子信道增益γ_{i∈（1，u）}及不同衰落因子m_{i∈（1，u）}的Nakagami衰落信道，错误概率可表示为

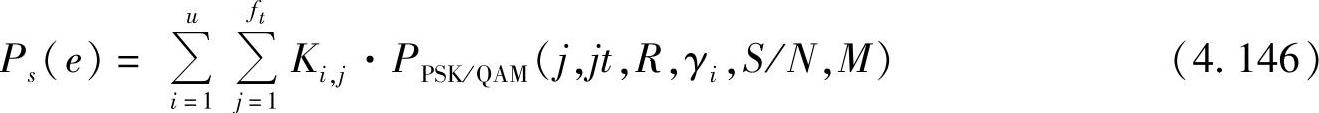
其中，系数K_i，j可通过对Nakagami衰落信道的MGF进行部分积分而获得^[467]。

（6）Nakagami衰落——一般子信道增益

此场景下的SER与具有不等子信道增益的瑞利衰落下的计算方法类似，因此在这里不再赘述。

4.3.1.3 端到端传输的最大吞吐量

假设中继使用估计转发或解码转发方案，且目的节点对接收信号的正确率进行判决，则可以利用上节获得的错误概率推导部分资源分配准则。这种转发方案与透明中继方案不同，在透明中继中信息只是经过简单的放大转发。这也与DF方案相异，因为DF的各个阶段都要进行基于接收信号正确率的判决。

如果DF的各个阶段的所有中继都在一个足够高的SNR下进行协同，则由前一阶段得到的信号采样值对所有中继都是相同的。因此，如果前一阶段的信号出错，则这个错误对属于同一阶段的所有中继都是一样的。

这种情形下前后相连阶段的错误相互独立，因而可以大大简化分析。这与通常的采用部分协同的中继过程不同，因为在部分协同时，一个中继的估计值可能比属于同一个R-VAA的其他中继更准确，因此不同阶段的错误并不独立。

最大化端到端吞吐量的问题等价于最小化端到端的BER问题，因而可以得出全部或部分协同情形下的部分资源分配准则。

假设源MS在每帧时间内经过K个中继阶段向目的MS传送B比特信息，归一化的端到端吞吐量可以表示为[467]

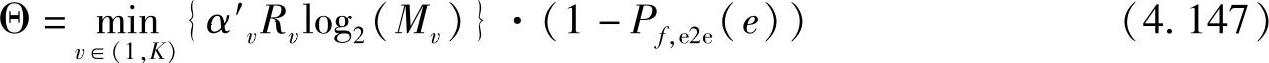
其中，α′_v、R_v和M_v分别是部分帧持续时间、STBC码率和第v个阶段的调制阶数；P_f，e2e（e）是端到端的误帧率。式（4.147）表明，如果S-D直连链路没有传输损失，那么全部B比特信息都可到达接收端，因此用全部发送的比特数进行归一化处理的吞吐量为1；在部分帧持续时间α′中采用调制阶数为M和速率为R的STBC码完成传输可以得到的归一化吞吐量为1·α′·R·log₂（M）（单位：bit（s·Hz））。由端到端误帧率P_f，e2e（e）引起的损失会相应地降低吞吐量。对具有K个中继阶段的通信系统而言，整个链路中最弱的一环决定了吞吐量，因而总吞吐量是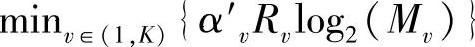，所以优化的目标是分析使得端到端吞吐量最大化的最优资源分配策略。

需要注意的是，P_f，e2e（e）是M_{v∈（1，K）}、R_{v∈（1，K）}（即min_{v∈（1，K）}{α′_v·R_v·log₂（M_v）}）及每一个阶段的部分传输功率分配的函数。由于式（4.147）所示的优化问题中的参数相当复杂，因而我们将优化过程分三个步骤进行。

●第一步：首先固定调制阶数M_{v∈（1，K）}，并只考虑SNR→∞的极限情况。式（4.147）可简化为

在满足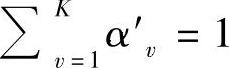的条件下通过选择部分帧持续时间α′_v使最大。显然，若所有的α′_vR_vlog₂（M_v）都相等，可以得到最大值，即(www.xing528.com)

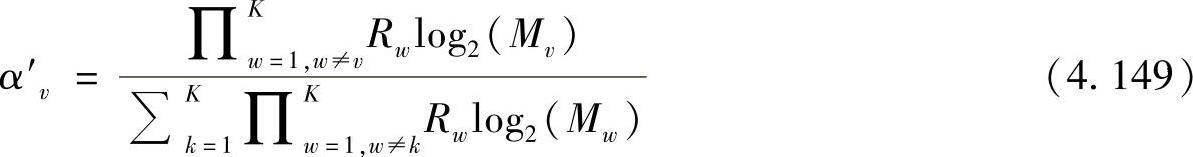
●第二步：在上述前提条件下，最小化端到端误比特率可以最大化吞吐量。假设比特错误相互独立，则归一化的吞吐量可以表示为

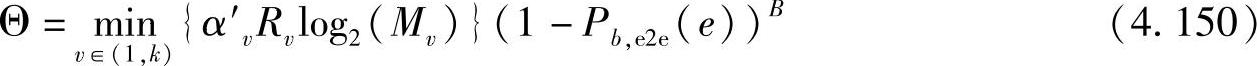
其中，B是每帧中的比特数。定义一个变量为Θ的非减度量

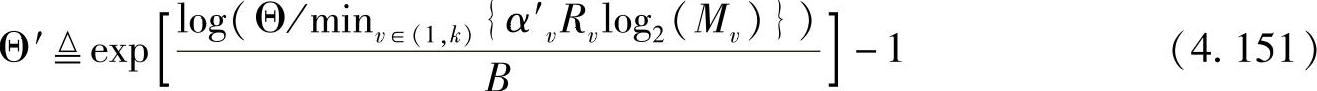
很容易得到

因此，若想最大化端到端吞吐量，就需要对每个中继阶段进行最优的部分传输功率分配以实现端到端误比特率的最小化。在误比特率或误符号率很小以至于一个符号错误只引起一个比特错误的情况下，每个阶段的误比特率与误符号率的关系为^[278]：

●第三步：根据已求得的部分资源分配确定最佳的调制阶数M_{v∈（1，K）}，这可以通过在每个阶段遍历所有可能的调制阶数的方式求得。由于调制阶数的数目有限，这种优化方法的计算复杂度并不太大，因而可行。

随后假设每一个阶段采用完全协同或部分协同。首先推导近似最优的部分功率分配准则，然后依据它们的精度进行评估，最后通过一些例子说明最大可达的吞吐量。

4.3.1.4 每阶段采用完全协同

在完全协同的假设下，K个中继阶段的每个阶段的误符号率P_{s，v∈（1，K）}（e）及其相应的误码率P_{b，v∈（1，K）}（e）相互独立。仅当一个比特从源经所有阶段都能正确传输时才能被目的端正确接收，因而端到端误比特率可以表示为

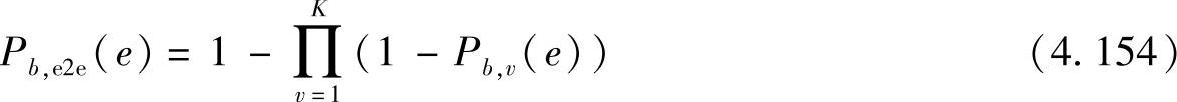
当每个阶段的误比特率都很小时，上式可近似为

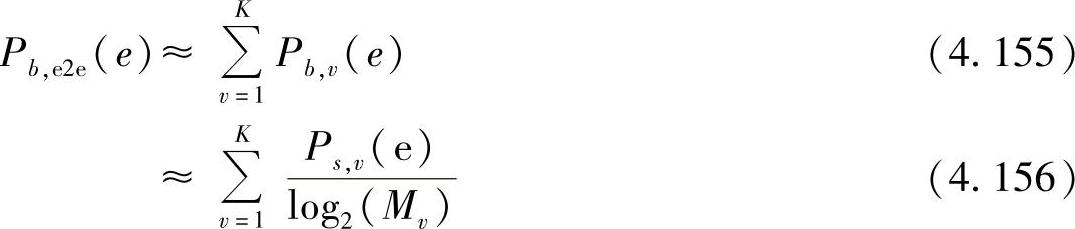
其中，M_v是第v个阶段采用的调制阶数。接下来主要分析每个中继阶段具有相等的信道增益且为瑞利信道的情况，而其他情况也可用类似的方法进行分析。假设分配给每个阶段的功率为β′_v，则误比特率可以表示为

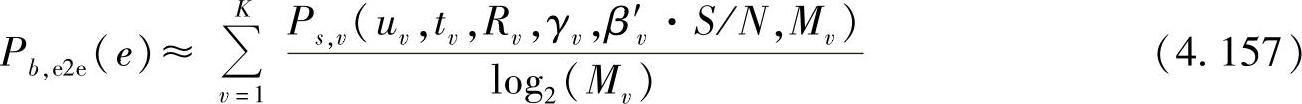
其中，误符号率P_s，v（·）=P_PSK/QAM（·）分别由式（4.137）和（4.138）给出；u_v≜t_v·r_v，t_v和r_v分别是第v阶段的发送天线数和接收天线数；R_v是STBC编码速率；γ_v是经历的平均衰落，S是信号从信源到信宿整个传输过程中的总功率；N是噪声功率。

这样最优化过程只需针对部分功率分配β′_{v∈（1，K）}进行。即使如此，最优化过程仍然十分复杂。为了进一步简化分析，我们利用M-PSK和M-QAM的误符号率上界。当θ=π/2时，式（4.134）可取得上界。在第v个中继阶段，M-PSK的误符号率的上界为

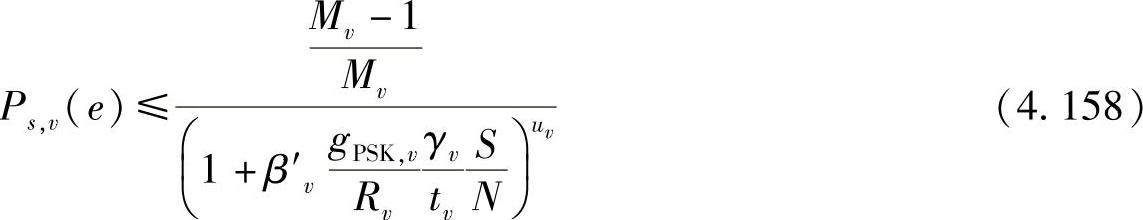
其中，g_PSK，v=sin²（π/M_v）。M-PSK调制方式的端到端误码率的上界为

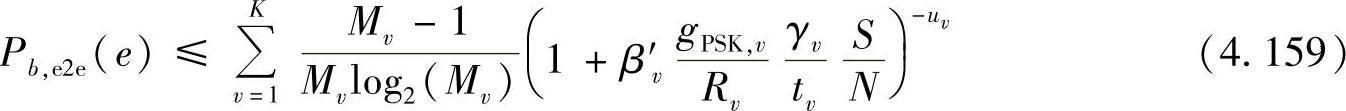
利用类似的方法，M-QAM调制方式的端到端误码率的上界为

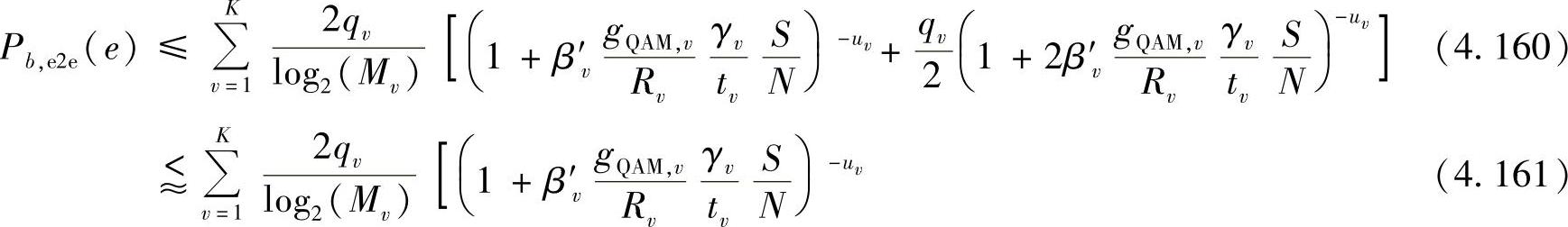
其中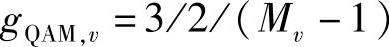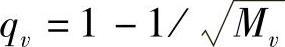，，。需要注意的是，在式（4.161）中，由于当x足够大且u_v≥1时，q_v/2＜1且（1+2x）^-uv比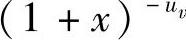小得多，因而式（4.160）中的第二个被加数可以忽略不记。两种调制方式的上界可以统一为

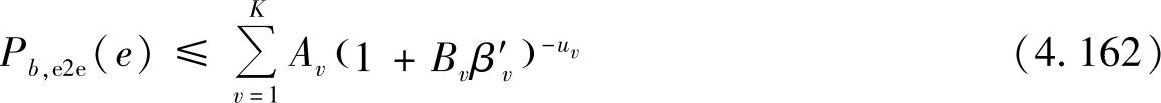
常数A_v和B_v可通过对比式（4.162）与式（4.159）得出

在文献[467]中指出，部分功率分配β′_{v∈（1，K）}需要满足

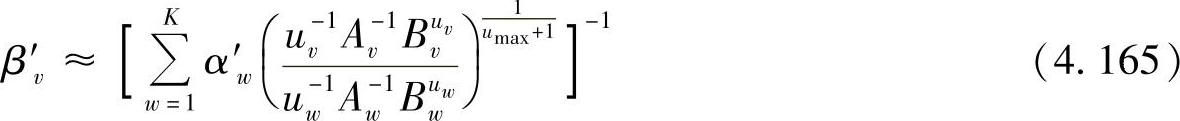
其中，u_max=max（u₁，…，u_K）。图4.30～图4.33仅在M-QAM调制方式下评估了提出算法的性能。需要指出的是，如果选择的参考方案并非是最优的，也仅是由于没有对部分传输功率分配进行最优化处理，因为帧持续时间很容易与调制阶数对应起来。

图4.30给出了端到端误比特率与第一条链路的SNR的关系，并比较了使用部分功率分配策略（由式（4.165）给出）的多种两阶段通信场景的性能，同时也给出了最优和非最优分配方案的数值解。

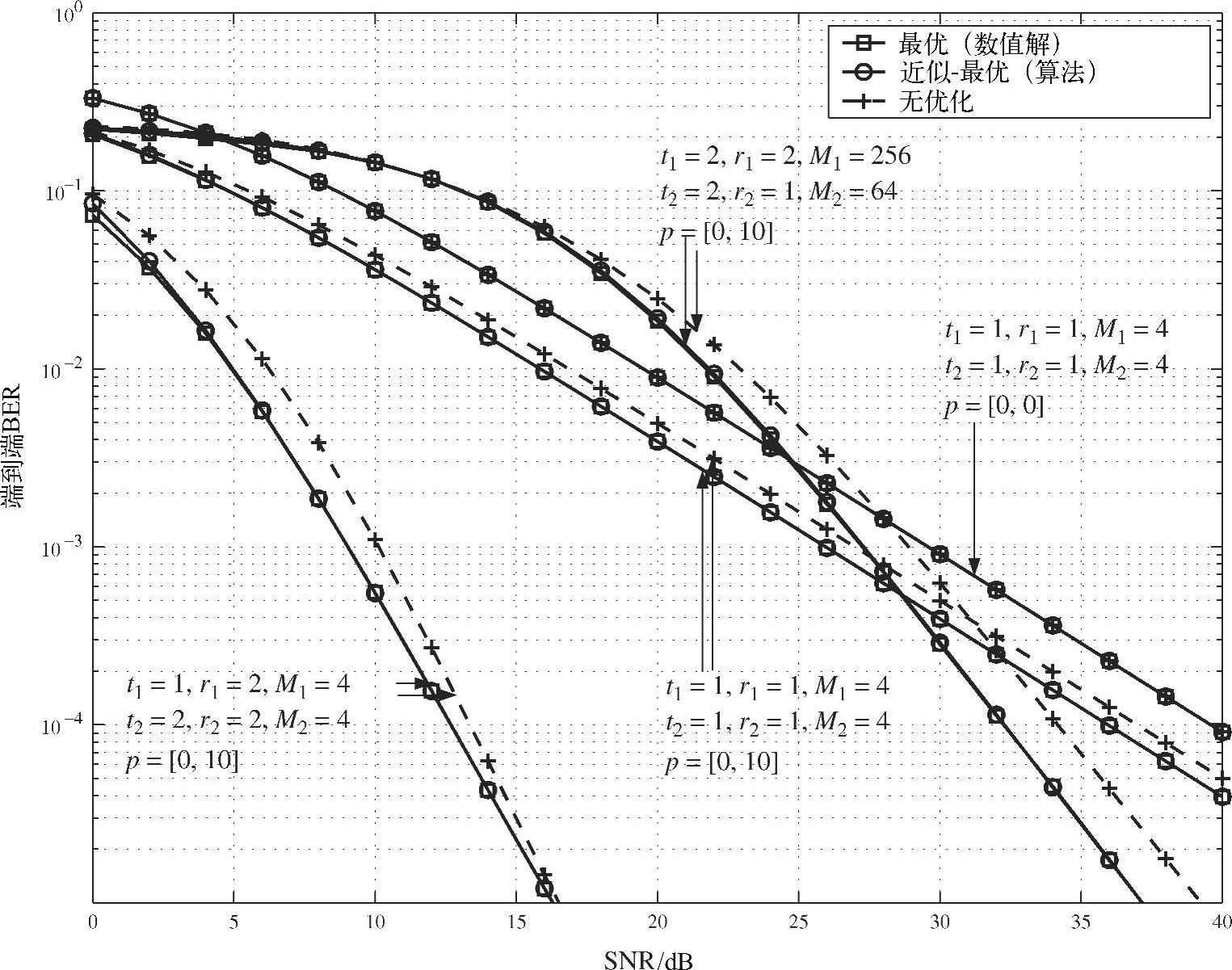
图4.30 不同配置下不同的两阶段中继方案的性能比较

第一种场景中，t_1，2=r_1，2=1，M_1，2=4（QPSK），p=[0，0]dB，这是完全对称的场景，因而三种功率分配策略的性能相同。第二种场景与第一种类似，区别在于第二阶段的信道比第一阶段好10倍，即p=[0，10]dB。这种非对称的场景使最优功率分配方案（实线）的性能

优于非最优功率分配方案（虚线）。

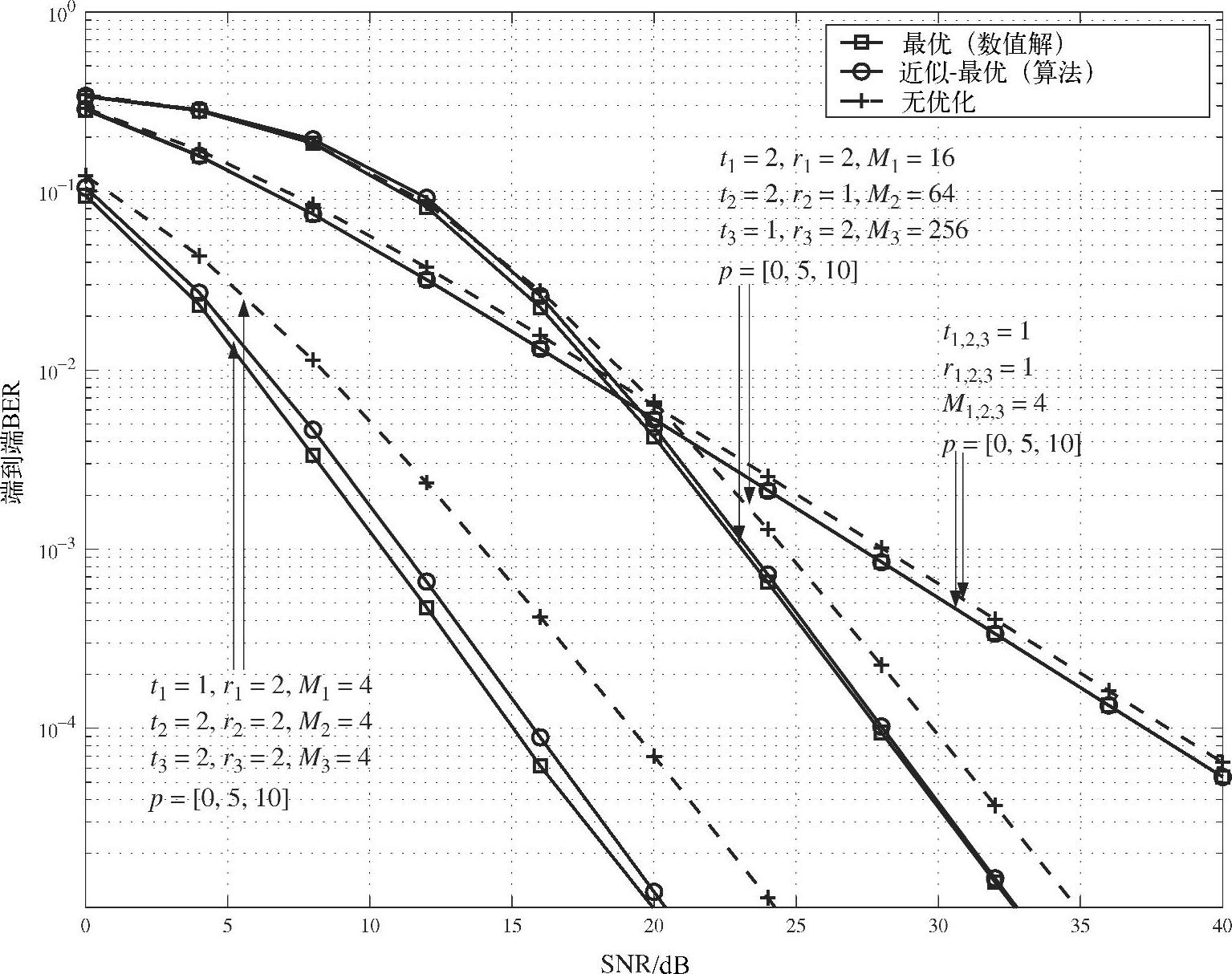
图4.31 不同配置下不同的三阶段中继方案的性能比较

可见在各种系统配置下最优策略与我们提出的分配策略都有相同的性能。此外，对于极不对称的场景，例如在仿真中t₁=2，r₁=2，t₂=2，r₂=1，M₁=256，M₂=64，p=[0，10]dB的配置下，最优方案与非最优方案的性能差最大，在端到端误比特率为10^-5时，最优方案可节省功率1dB。

在本质上图4.31与图4.30相似，唯一的区别是图4.31仿真的是具有三阶段的中继网络。在这些场景中可以观察到类似的结论，但增益几乎达到4dB，这说明所提出的分配策略非常有效。

图4.32是两阶段系统的吞吐量曲线，使用了式（4.149）与式（4.165）给出的部分资源分配策略。仿真系统参数配置为：发送到信息比特数B=100，调制方案为M_1，2=4（QPSK），p=[0，10]dB。从仿真结果可见，低SNR时，提出的分配策略比最优策略稍差，这是因为部分帧持续时间是在SNR→∞的前提下求得的。

对于大多数从零到最大吞吐量的过渡区域，所提出的分配策略达到近似最优的吞吐量。与之形成鲜明对比的是，没有优化的方案在过渡区域存在显著的性能损失。例如第一条链路的SNR为6dB、t_1，2=r_1，2=2时，大约有0.4 bit（s·Hz）的损失，约为40%。

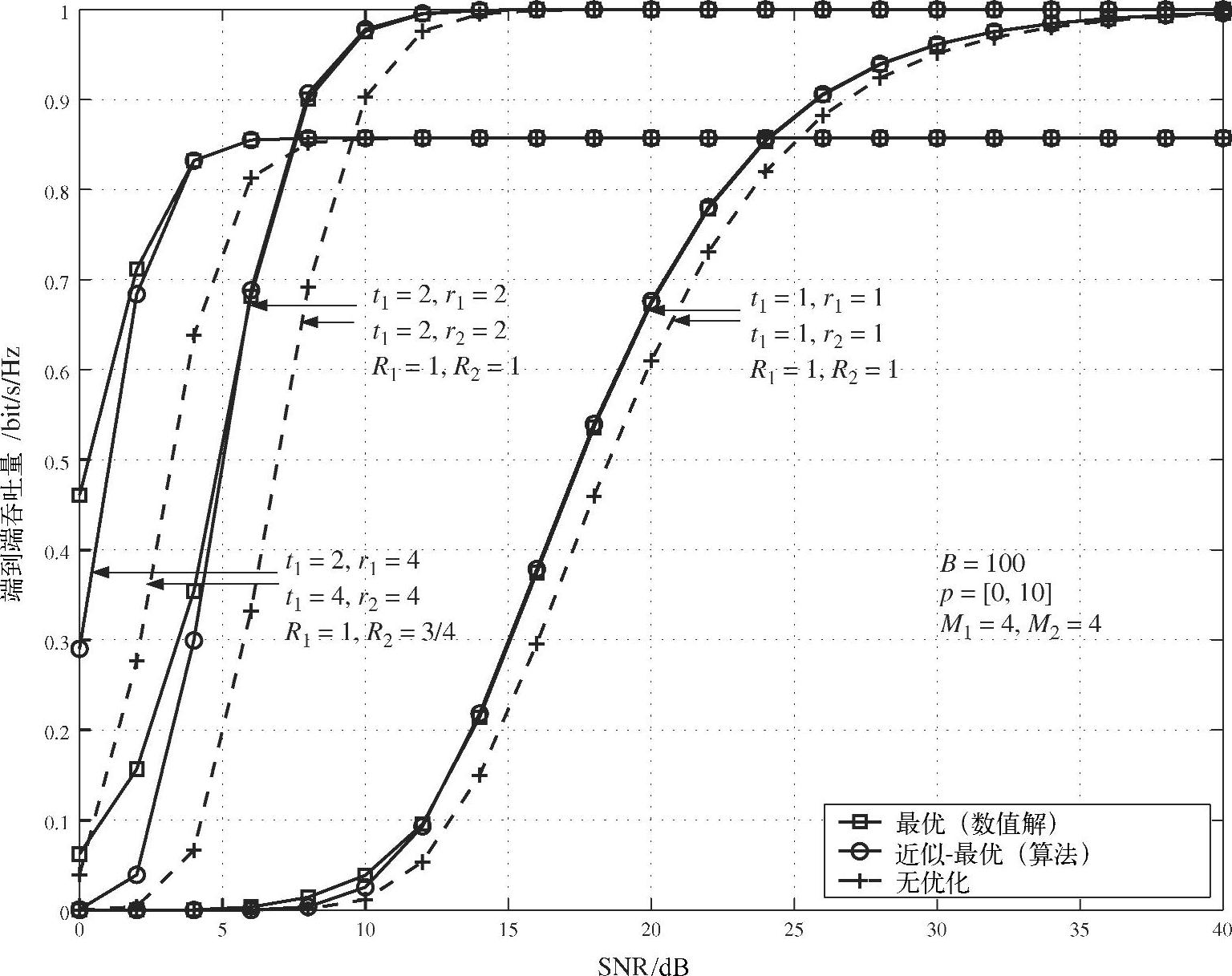
图4.32 二阶段中继网络不同系统配置下不同方案的端到端吞吐量对比

此外还注意到，在每一阶段采用满速率STBC方案的系统具有相同的最大吞吐量，而对于3/4码率的STBC方案，即使在（2×4）/（4×4）的最好链路条件下，其最大吞吐量相对满速率STBC方案依然要低，很显然这是由于其速率小于1从而频谱效率受限。显然，链路质量决定了系统逼近其极限速率的程度，而极限速率是指SNR→∞时系统可以达到的吞吐量。

对于固定的调制阶数，部分分配算法能够在每一个中继阶段获得最终的数值最优解。式（4.149）和式（4.165）的低复杂度保证了只需要较少的额外计算量就可以获得最优的结果。

我们以p=[0，10]dB、t_1，2=r_1，2=2的两阶段中继网络为例进行数值最优化计算。每个阶段都可以在集合M_1，2=（2，4，16，64，256）中选择一个调制阶数，这样一共有25种可能的组合，这可在一秒内计算出来。图4.33所示的结果可以清楚地看到最优的自适应调制方案相比固定阶调制组合方案在吞吐量性能上的增益。任意SNR下，提出的算法都远好于固定调制阶组合方案。例如，第一条链路的SNR为20 dB时，固定调制阶方案最多能达到2 bit/s/Hz，此时两个阶段采用16-QAM或64-QAM，而最优部分功率分配下的最佳选择是64-QAM，性能增益可以达到30%。

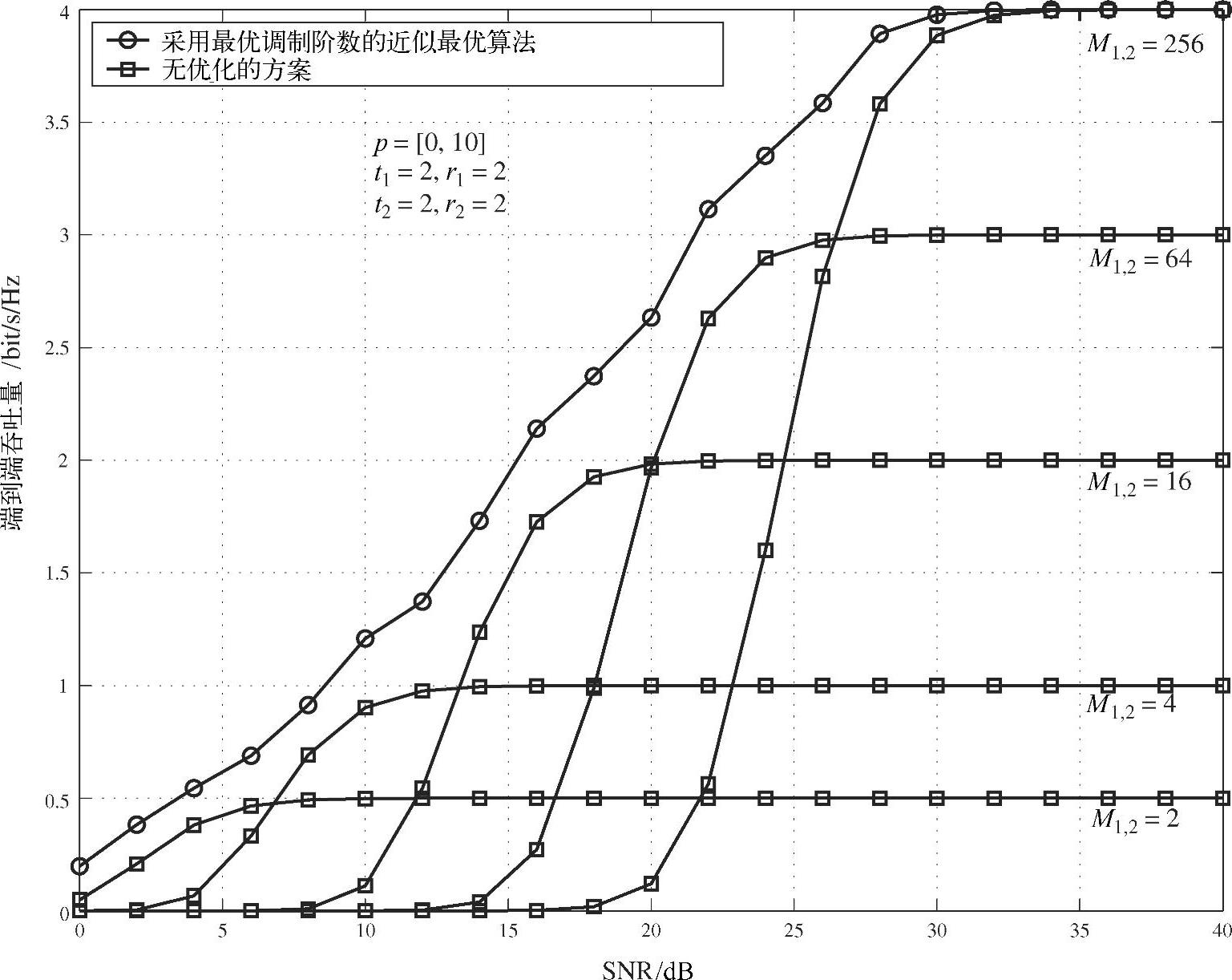
图4.33 与无优化系统相比，在M_1，2=（2，4，16，64，256）中自适应选择调制阶的数值优化方案能获得近似最优的端到端吞吐量

4.3.1.5 每个阶段采用部分协同

在每个转发阶段采用部分协同使得信道成为具有不同强度的并行MIMO信道。图4.34示意了一个部分协同的处理过程的例子，其中参与处理过程的中继不与其他任何中继协同。第一阶段包含两个独立的SISO信道，其平均衰落分别为γ_1，1和γ_1，2，每个信道的误比特率P_1，1和P_1，2相互独立。第二阶段包含两个独立的MISO信道，其中第一个MISO信道由平均衰落分别为γ_2，1和γ_2，3的两个信道组成，第二个MISO信道由平均衰落为γ_2，2和γ_2，4的两个信道组成。另外，假设送入第二个VAA中继层的信息无差错，MISO信道输出的信号的误比特率分别为P_2，1和P_2，2。在最后的第三阶段包含一个单独的MISO信道，其误比特率为P_3，1。

需要注意的是，属于同一阶段的中继以相同的速率进行数据传输，此外还需知道各自发送的是空时分组码的哪一部分。在这里依然假设所有终端都是精确同步的。

获得精确的端到端误比特率很重要，因为第一阶段产生的错误可能会传播到目的端，也可能在后一阶段被纠正。例如在图4.34中，假设相同的比特经链路（1，1）后被错误接收，经链路（1，2）后被正确接收，因而经由链路（2，1）和（2，3）输出的信息形成STBC时有一路错误的输入和一路正确的输入。如果γ_2，3＞＞γ_2，1，则错误不会继续传播；但如果γ_2，3＜＜γ_2，1，则很可能错误会继续传播下去。这样每个阶段的错误概率与所用的调制方案、占优势的信道统计特性、平均信道衰落以及采用的STBC方案都有关。在分析端到端误码率性能时，有必要对这些复杂的相互关系进行适当的简化。

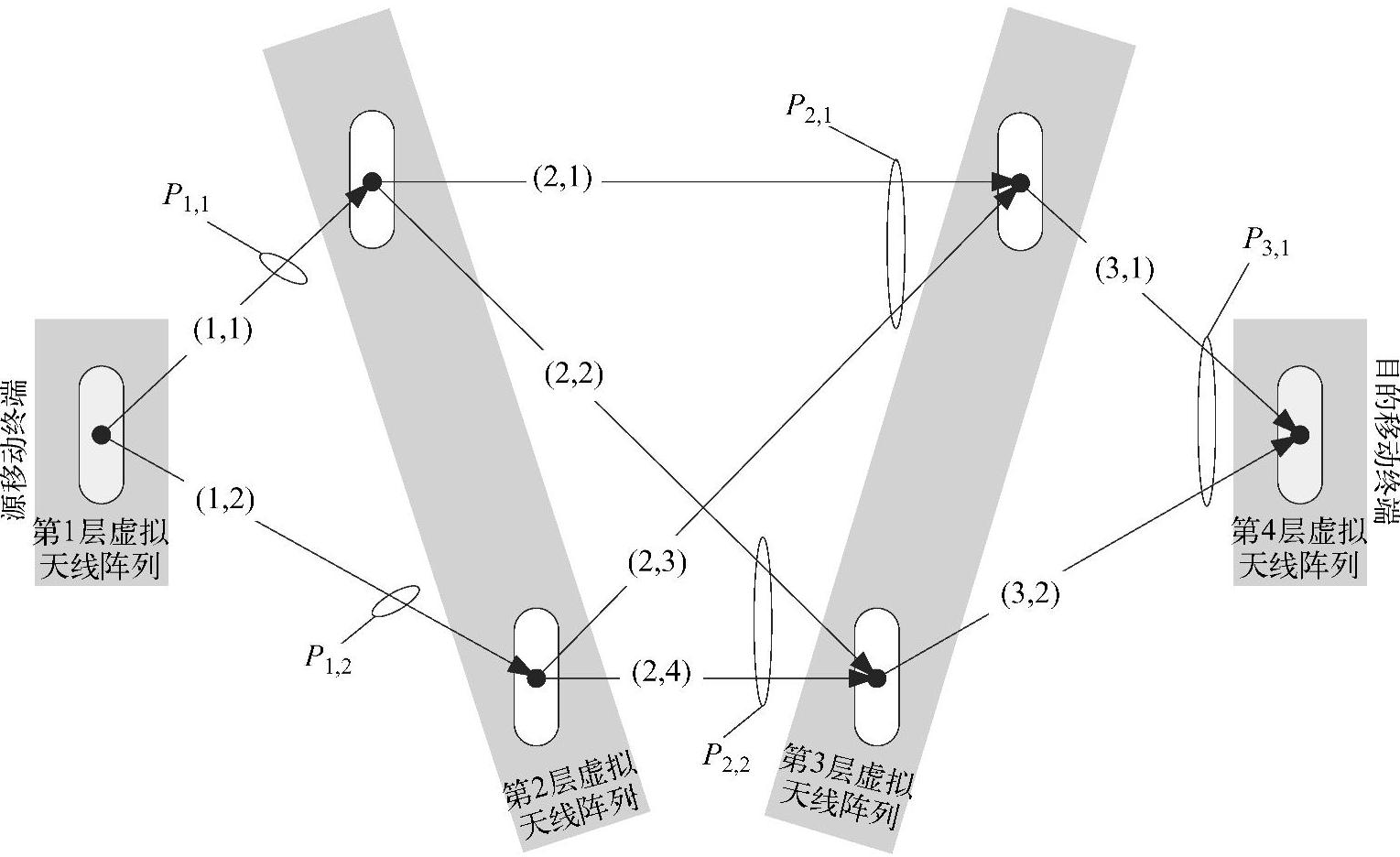
图4.34 三阶段无协同分布式空时分组码MIMO通信系统

通常希望获得各阶段相互分离的错误概率的近似表达式。为此，假设系统的错误率很低，从而整个网络在同一时刻只发生一个错误。假设错误发生在链路（1，1）上，链路（1，2）无差错发生，则错误传播发生的概率与信道（2，1）和（2，3）的强弱有关。Ri-beiro、Wang和Giannakis在文献[275，383]中的渐近分析表明，错误传播概率正比于发送STBC部分码字的分支信道强度，在本例所示的两个MISO信道中，一个分支信道是链路（2，1），另一个分支信道是链路（2，2）。因此，以概率P_1，1在链路（1，1）上发生的一个错误，在由链路（2，1）和（2，3）构成的O-MISO信道传播下去的概率为P_1，1·γ_2，1/（γ_2，1+γ_2，3），其中出错信道（2，1）的能量已用两个子信道的总能量进行归一化处理。为了获得传递到目的端的错误概率，需要遍历网络中所有的可能路径，然后用每条路径的增益比值对初始错误概率进行加权。

考虑上述因素并假设SNR较高，即任意一条链路只可能发生一个错误，则图4.34所示的中继网络的端到端BER可表示为

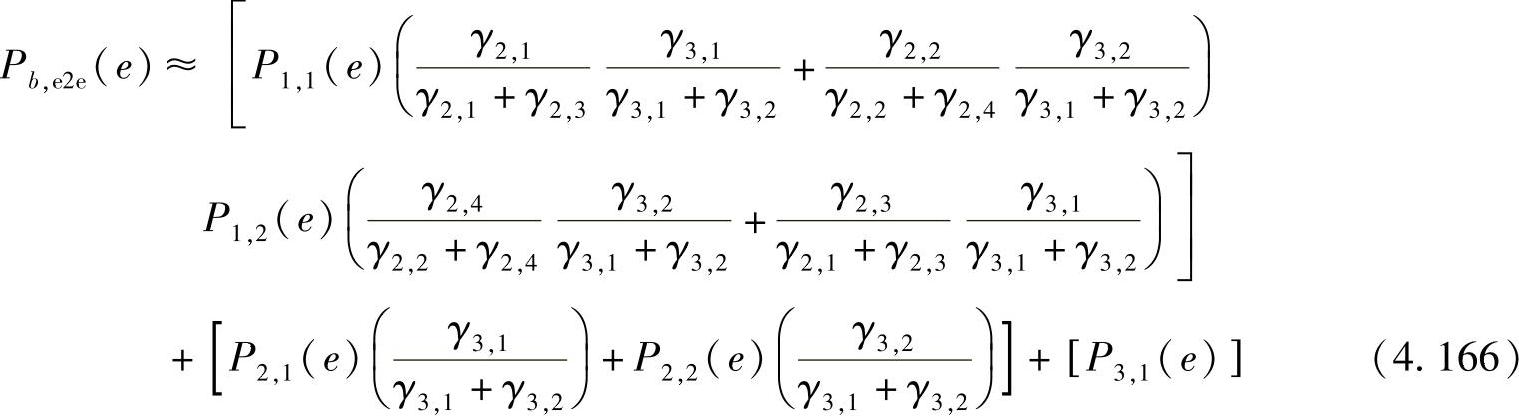
上式可以简化为

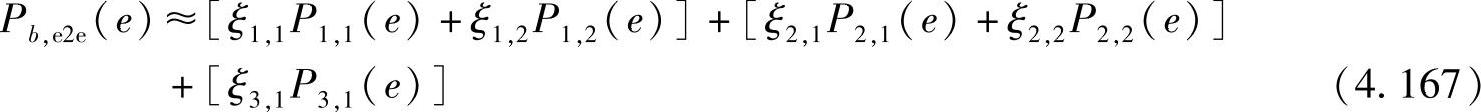
其中，ξ_v，i是在链路（v，i）上产生错误并传递到目的端的概率。这个结果很容易推广到具有任意规模、任意部分协同形式的中继系统。注意到第v阶段有Q_{v∈（1，K）}个协同簇，每个协同簇产生一个错误的概率为P_{v∈（1，K），i∈（1，Qv}），端到端的误比特率可近似为

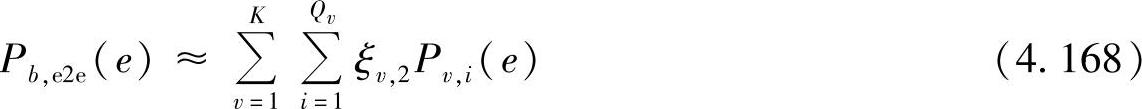
其中，概率ξ_v，i可以根据特定的网络拓扑计算出来。误比特率P_v，i（e）可以由式（4.153）、具有适当收发天线数的簇的误符号率，以及占优势的信道条件计算出来。我们在图4.35和图4.36中验证了推导得到的端到端误比特率公式。

针对图4.34所示的并去除第二阶段而成的两阶段中继网络，图4.35比较了分别通过理论计算与数值仿真得到的端到端误比特率与第一跳链路的SNR之间的关系。所有仿真系统采用的调制方式为QPSK，图中标注的是各个信道的增益。从图中的性能曲线可见，在低SNR区域，理论计算与仿真所得的BER存在差距，但随着SNR的增大，两条曲线渐渐汇合。

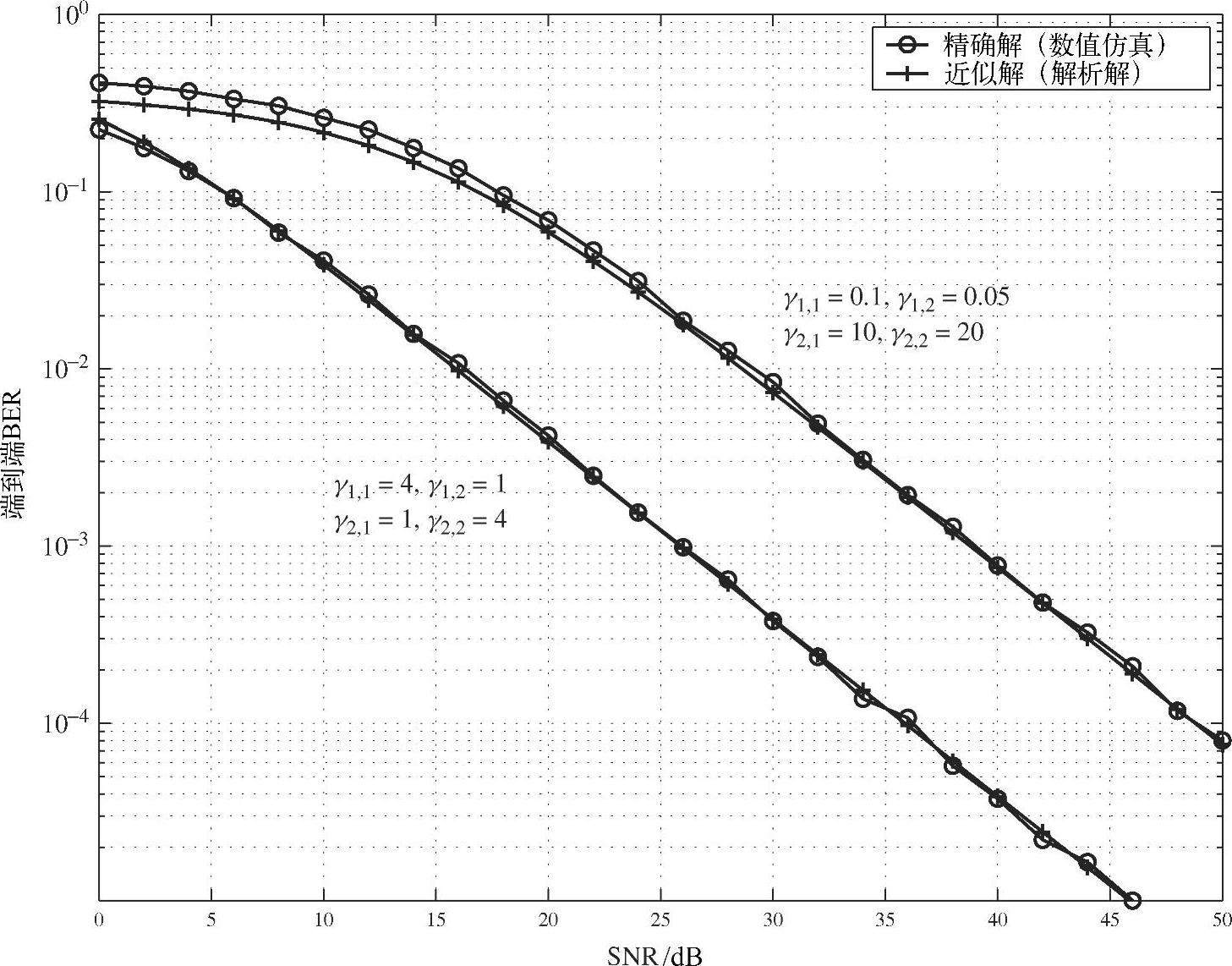
图4.35 两阶段无协同网络端到端BER与第一跳链路的SNR之间的关系

图4.36比较了图4.34所示的三阶段中继网络的分别通过理论计算与数值仿真得到的端到端误比特率与第一条链路的SNR之间的关系。同样，曲线上标注的是信道增益。从图中可见，在各种场景下理论计算所得的BER具有很高的准确度。

由式（4.168）给出的端到端BER，我们可以确定最优部分功率分配β′_{v∈（1，K）}和部分帧长α′_{v∈（1，K）}，从而获得近似最优的吞吐量。在高SNR区域，部分帧长独立于信道统计特性或协同度，因此式（4.149）对α′_{v∈（1，K）}也成立。下面对部分功率分配进行推导。

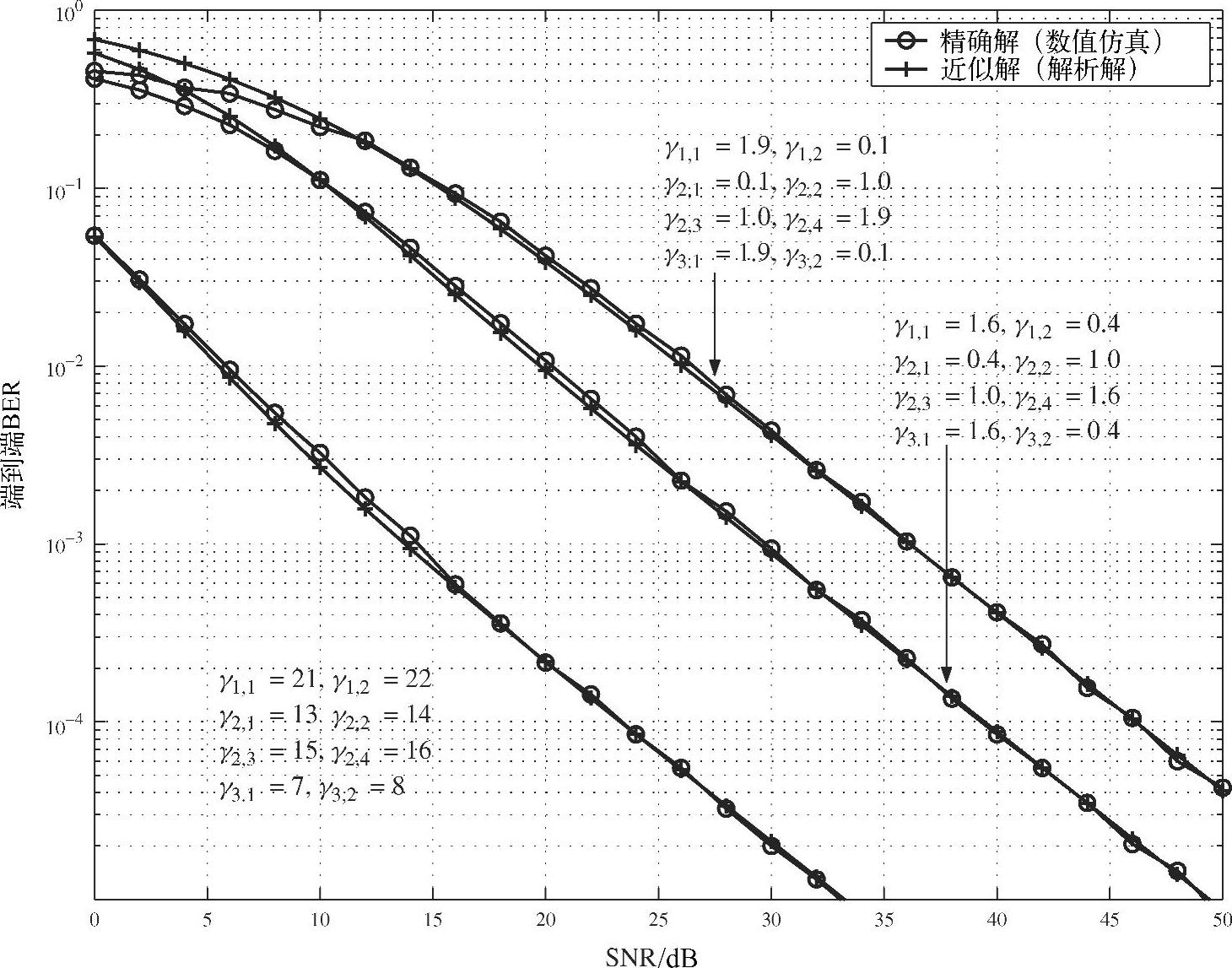
图4.36 三阶段无协同网络端到端BER与第一跳链路的SNR之间的关系

不失一般性，假设所有链路都服从瑞利衰落，并且具有不同的信道增益。式（4.141）给出了错误概率，其中u必须由簇Q_v中的子信道数代替。因此部分功率分配为

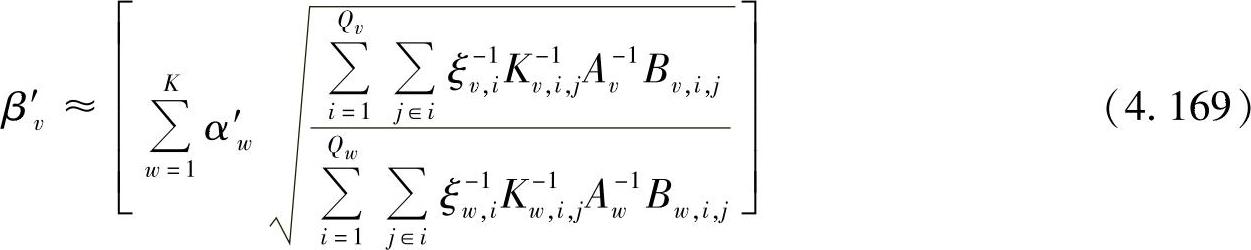
其中，j∈i表示第i簇的第j个子信道。第i簇的第v阶段的K_v，i，j可以写成

式中共有u_v，i个乘法项。常数A_v由式（4.163）给出，其中

需要指出的是：在上述优化过程之前并没有应用注水法进行功率分配。从仿真结果来看，采用注水法的功率分配方案并没有带来明显的性能提升，这也是我们在以上的分析过程中忽略注水法的原因。