软信息转发协议：实现高效信息传输

前面讨论了多种常用的中继转发协议，采用AF协议的中继在放大信息信号的同时也放大了噪声，因此AF的主要缺陷是噪声放大效应。如果S-D链路的信道质量足够好，中继可以正确译码并能完全恢复源信息。此时采用DF协议的中继正确译码并重编码则可以完全避免噪声放大效应，因而DF协议的性能优于AF协议。然而，当S-R链路的信道质量较差从而中继存在译码错误时，那么DF协议将产生严重的误判传播从而导致系统性能显著下降，此时AF协议性能很可能优于DF协议。为充分利用AF与DF的优点并避免其缺陷，本节将讨论能进一步提高中继系统性能的增强型再生中继协议，即软信息转发协议、自适应转发协议，以及下节将介绍的选择式译码转发协议。

我们已经知道，当中继处存在译码差错时，译码并重编码处理将产生误判传播从而恶化DF协议的性能。为抑制错误传播，可计算并转发软信息以代替硬判信息。中继计算并转发软信息替代不可靠的硬判信息可以为目的节点译码器的译码判决提供附加信息。这种协议称为软信息转发（SIR）协议。文献[454-462]研究了多种SIR协议并应用于不同的系统。在本节中，我们首先介绍SIR协议的系统模型，然后介绍几类SIR协议及其表示和建模方法，最后通过仿真评估这些SIR协议的性能。

类似于前面的讨论，我们考虑简单的两跳中继网络，它包括一个源节点、一个中继和一个目的节点。不失一般性，我们考虑卷积编码系统。将编码系统中的码字自由距离替换为未编码系统中的信号星座图的最小欧氏距离，就可以很容易地将编码系统推广到未编码系统。

在源节点处，二进制信息序列首先经卷积编码器编码为码字C=（C₁，…，C_k，…C_L），其中L为码字长度，C_k是第k个编码符号且对于M-QAM调制，C_k∈{0，1，…，M}。C_k经调制后得到x_k，且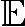{|x_k²|}=1。再将x_k广播至中继和目的节点，中继和目的节点处相应的接收信号y_SR，k和y_SD，k分别为

其中，p_SR与p_SD分别是中继和目标节点处的接收信号功率。此外，h_SR和h_SD分别是S-R链路和S-D链路的信道衰落因子，假设都为零均值、独立循环对称复高斯随机变量。考虑准静态衰落信道，即衰落系数在一帧内保持不变，而在帧间独立变化。n_SR，k和n_SD，k是零均值复高斯随机变量，其双边功率谱密度为N₀/2。对于SIR，中继对来自源节点的信号进行译码并计算x_k的软估计值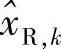。中继转发的信号表示为

其中，β是放大系数，它可根据中继的发射功率限制来求得，即

其中，p_R是中继的发射功率限。目的节点对应的接收信号y_RD，k为

其中，G_RD和h_RD是R-D链路的信道增益和衰落系数，n_RD，k是零均值复高斯随机变量，其双边功率谱密度为N₀/2。目的节点合并分别来自源节点和中继节点的信号并译码从而恢复原始信息比特。

有多种方式表示软信息，我们介绍两种常用的软信息的表述方法，即基于符号软估计（SIR-SSE）和对数似然比（SIR-LLR）的SIR。

4.2.3.1 基于符号软估计的SIR

首先考虑基于符号软估计的SIR协议^{[454，456，459-462]}。设源节点的第k个编码符号为C_k，k=1，…，L，x_k=Mod（C_k）是C_k的调制信号，其中，Mod（·）表示调制函数。P_r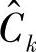（=jY_sr）表示中继译码器的输出为j（j=0，…，M-1）的后验概率（APP），其中，Y_sr是中继的接收信号序列。采用MAP译码时，可以用下式计算APP：

其中，h是使∑_jP_r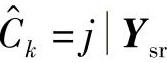（）=1的常量；m和m′是格图中与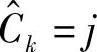相连的状态变换对；Ms是格图的状态数；γ_k（m，m′）是格图中连接状态m和m′的分支度量；α_i（m′）和β_i（m′）是前馈和反馈递归变量，它们可以通过以下两式进行计算：

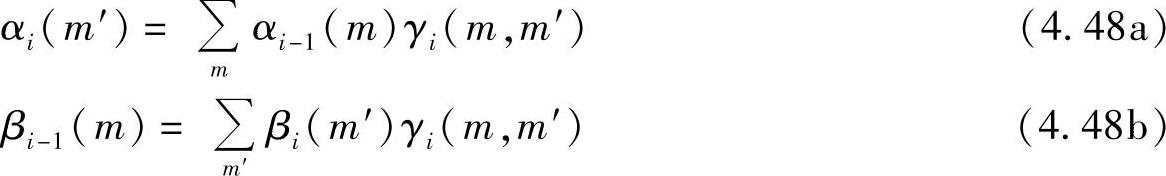
由此，中继对x_k的软估计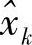为

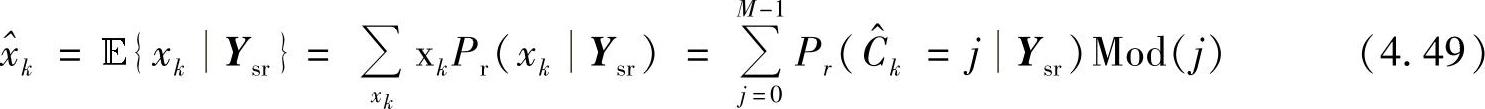
下面的定理证明了SSE是满足最小均方误差（MMSE）的估计^[461，462]。

定理4.2.1：式（4.49）所示的符号软估计是MMSE估计。因此，SIR-SSE是一种最优的无条件MMSE中继协议。

证明：令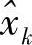表示x_k的估计值，则均方误差（MSE）为

以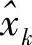为变量对上式求导可得

这就证明了：如果不对做任何限制，那么式（4.49）表示的符号软估计是MMSE估计。为简化起见，下面我们考虑BPSK调制方式，并将0和1分别映射为1和-1。那么，x_k的符号软估计值为：

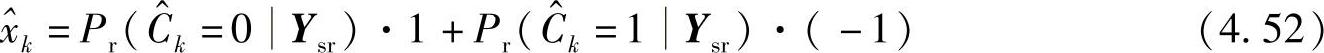
可以将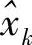表示为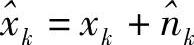，其中x_k是源节点发送的真实符号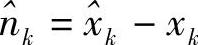，是等效噪声，可将其建模为零均值、方差为的随机变量。如果x_k和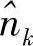相互独立，那么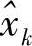的平均功率为

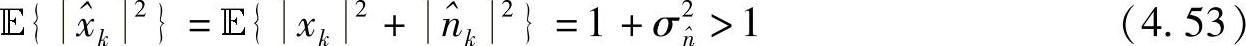
然而，对于BPSK调制，式（4.52）中-1≤≤1，且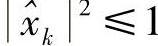，与式（4.53）相矛盾。这意味着x_k和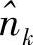实际上并不独立。文献[454，461]也证实了这一点。接下来我们介绍这两篇文献给出的两种关于相关性的建模方法，虽然两种建模方法各不相同，但从后面的分析可以发现，两者的本质相同。

（1）第一种SSE建模方法

Gomadam和Jafar^[461]通过在SSE中引入一个系数来表征期望信号与等效噪声间的相关性，并将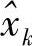表示为

其中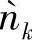，为新模型中的等效噪声；α_x是一个标量，称为相关性标量，表征了期望信号x_k和等效噪声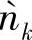之间的相关性。正如我们在后面所看到的，α_x≤1，这表明中继处有效信号功率从1降为α²_x。有效信号功率的降低实际上是由于中继的检测错误造成的。在下文中我们将这种SSE建模方法称为“SSE-标量”，并将利用这个模型的SIR中继协议称为“SIR-SSE-标量”。接下来我们计算相关性标量α_x，使得

由式（4.54）有

将式（4.56）代入式（4.55），有

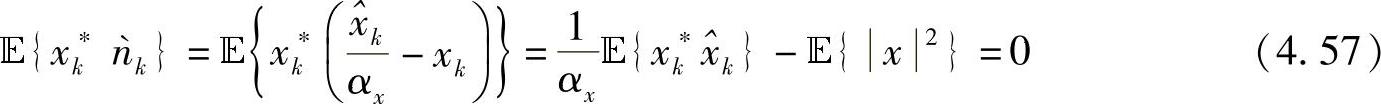
求解上式可得

通过式（4.56）和（4.58），很容易可证明下式成立：

将式（4.58）代入式（4，54），则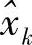为

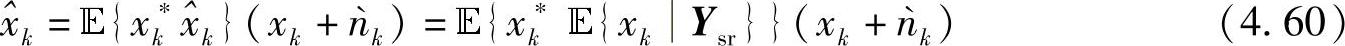
则中继转发的信号为

其中，β为归一化系数。x_R，k满足中继的发射功率限制，即

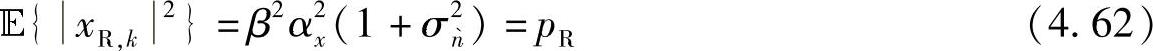
其中，p_R是中继的发射功率限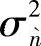；是的方差，可以按下式计算：

由（4.62）可知

中继转发信号x_R，k所对应的目的节点的接收信号为

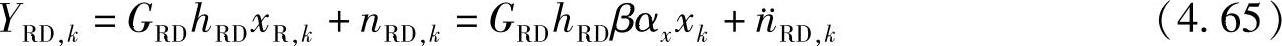
其中，

是目的节点的等效噪声，其均值为0，方差σ²_D为

现在我们来分析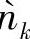的分布。由于h_SR只影响中继的接收SNR而不改变n`<sub>k</sub>的分布，所以只需要评估当h<sub>SR</su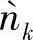b>值固定时的的分布即可。为了简化起见，设h<sub>SR</sub>=1，即在AWGN信道下评估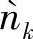的分布。不同的E<sub>b</su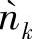b>/N<sub>0</sub>条件下的概率密度函数如图4.4所示，其中采用码率为1/2、状态数为4、生成矩阵为（1，5/7）的RSC码。需要指出的是，不服从高斯分布，而服从对称的双峰分布，是两个具有相同方差但均值相反的正态分布的叠加。随着E<sub>b</sub>/N<sub>0</sub>的增加，两个峰尖逐渐靠近，最终在高SNR时逼近为正态分布。正如我们在后面将要看到的，该模型下等效噪声的分布与接下来要介绍的第二种建模方法中的等效噪声的分布非常类似。因此，我们不在这里详细讨论n`_k的分布，而将其留在第二种建模方法的介绍之中。

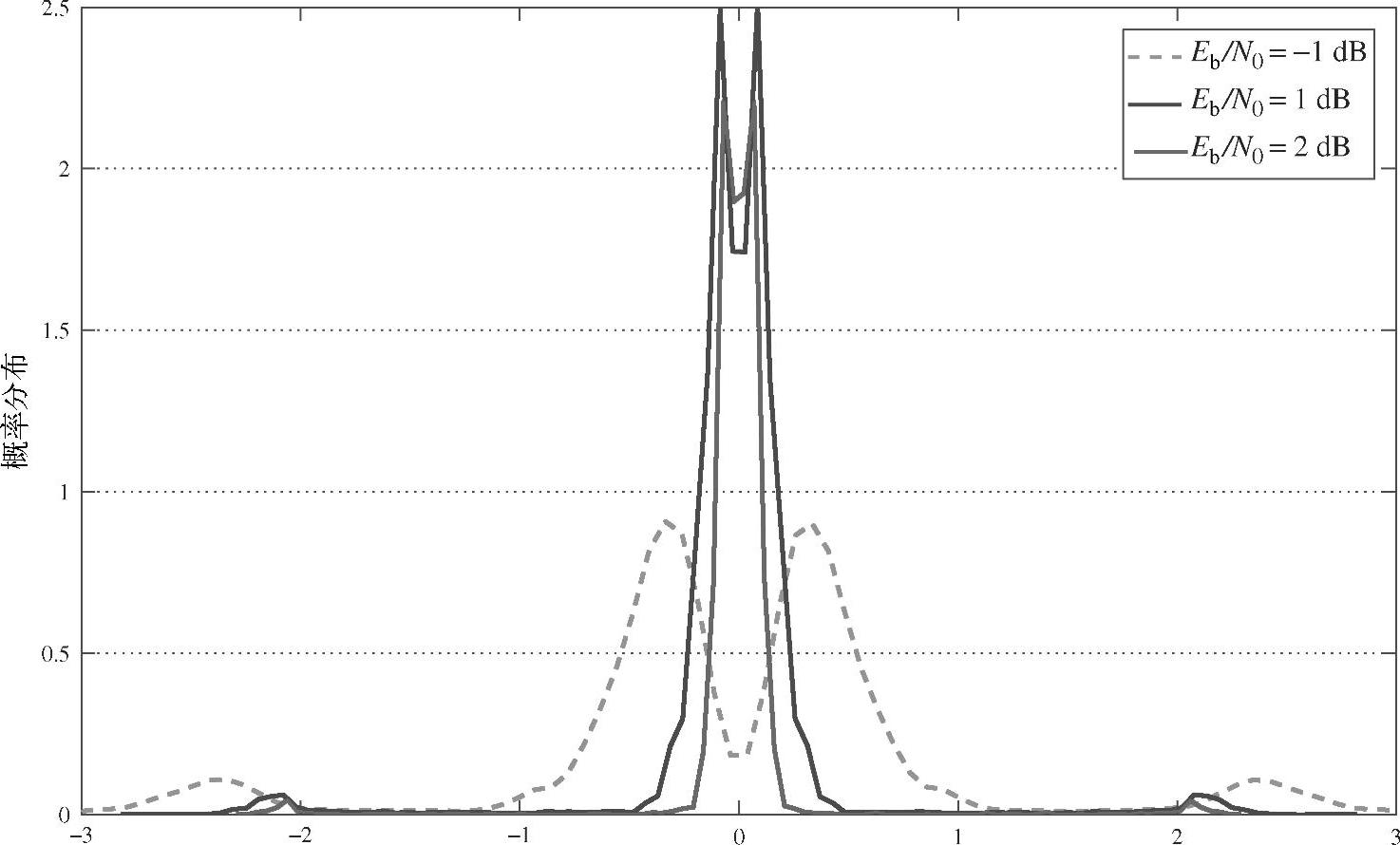
图4.4 中继处符号软估计的等效噪声n`_k的分布

（2）第二种SSE建模方法

在SSE协议中，同样考虑到期望信号和等效噪声间的相关性，文献[454]提出了另一种的等效模型：

其中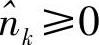，是新模型的等效噪声，其均值为

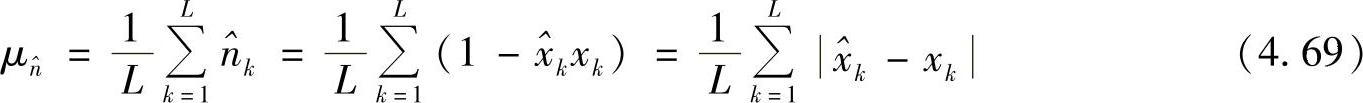
方差为

在下面的讨论中，我们将这种建模方法称为“SSE-新模型”，并称利用此模型的SIR协议为“SIR-SSE-新模型”。

在这个模型下，中继转发的信号表示为

其中，β值可以根据在中继处的功率限制来获得

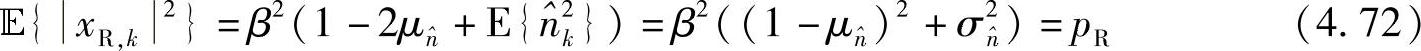
令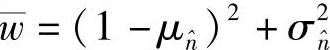，由式（4.72）可得

目的节点的接收信号可表示为

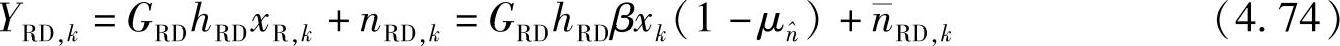
其中，

为目的节点的等效噪声，其均值为0，方差σ²_E为

在式（4.74）中，发射信号x_k的系数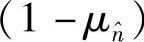≤1，该系数实际上降低了接收信号的等效信号功率，这也是因为中继处存在错误检测而造成的。这同前面讨论过的SIR-SSE-标量建模方法中的相关性标量α_x的作用非常相似。实际上，我们可以通过下面的定理证明α_x等于（1-μ_n^）。

定理4.2.2 符号软估计中，SSE-新模型中的等效噪声的均值和SSE-标量模型中的相关性标量α_x有如下的关系：

证明：比较式（4.54）和式（4.68）所表示的两种软符号估计建模方法，可以得到

将等式两边乘以x_k，得

进一步可写成

对等式两边取期望，有

这个定理本质上说明SSE-新模型和SSE-标量模型是相同的，即由一个模型可以计算出另一个模型的参数。接下来我们还将发现两个模型的噪声有非常相似的分布。令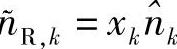，考察的分布。不同E_b/N₀时的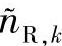分布密度如图4.5所示，仿真参数与图4.4的相同。由图可知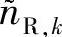，的分布近似为高斯分布。(https://www.xing528.com)

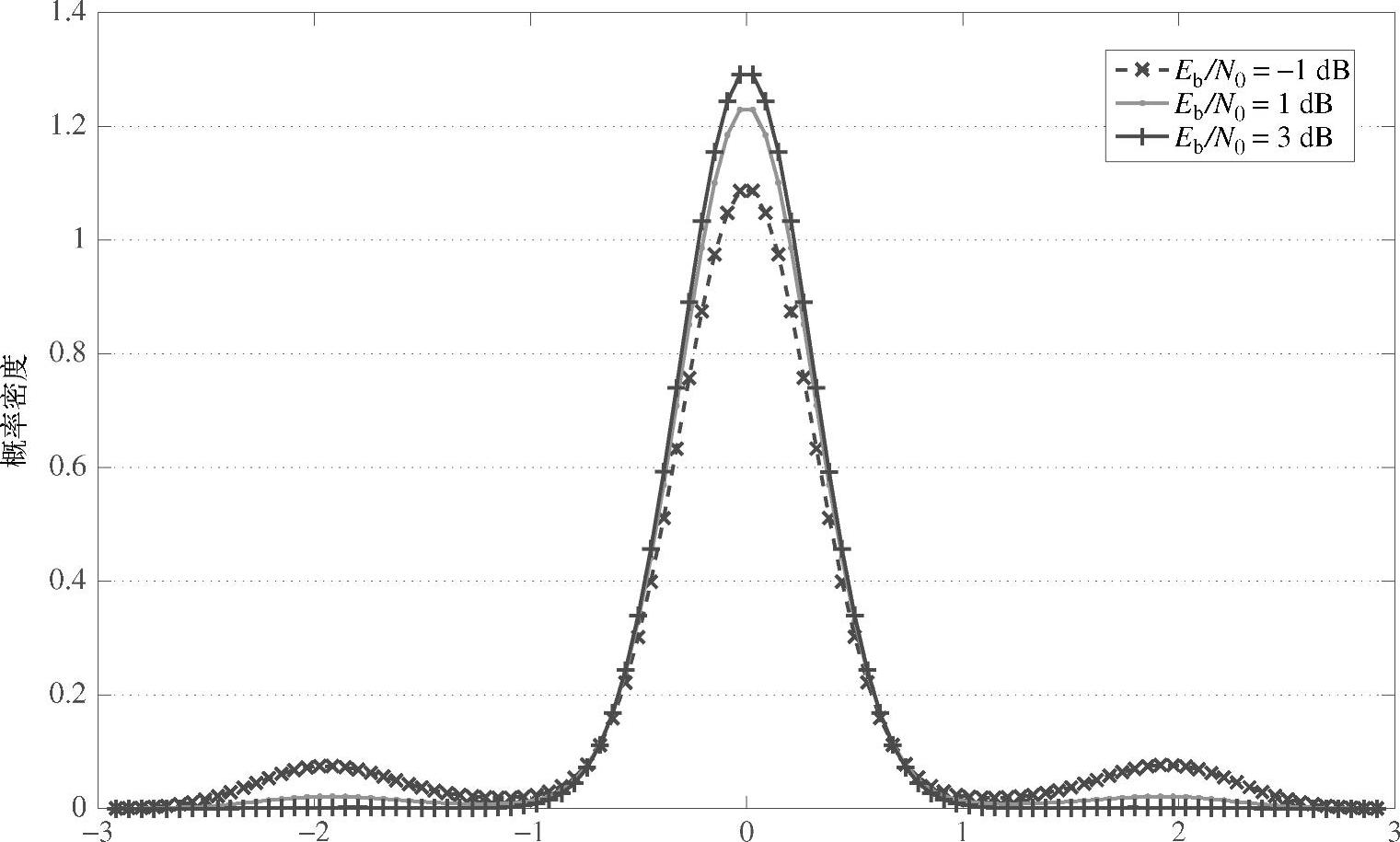
图4.5中继处符号软估计的等效噪声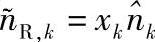的分布

类似地，令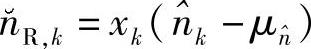，其分布如图4.6所示。将该图与前面介绍的SSE-标量模型的等效噪声分布图4.4比较，可以发现它们有非常相似的分布，即都服从对称双峰分布。因此，接下来我们主要关注SIR-SSE-新模型，因为相似的现象和处理也都可以应用于SIR-SSE-标量模型。

图4.7比较了和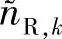的分布，其中曲线“E_b/N₀=1dB（包含均值）”表示当E_b/N0=1dB时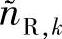的分布，“E_b/N₀=1dB（不包含均值）”表示当E_b/N₀=1dB时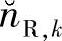的分布。

当E_b/N₀=-1dB且n_RD，k的方差是的1/10时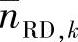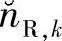，、和n_RD，k的分布如图4.8所示。类似地，当E_b/N₀=-1dB且n_RD，k与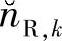的方差相等时，三者的分布如图4.9所示。在这两张图中，“目的节点处总噪声的分布”、“符号软估计中噪声项的分布”以及“目的节点接收机的噪声分布”分别表示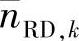、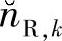和n_RD，k的分布。

由这些图可知，虽然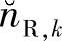并不服从高斯分布，但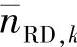近似服从高斯分布，甚至当目的节点接收机的噪声n_RD，k远小于时。由于很难得到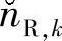的精确分布，为了简单起见，我们假定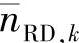服从高斯分布。由后面仿真结果可知，虽然高斯分布不是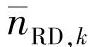分布的最优估计，但它确实能提供非常好的性能结果，并且优于其他符号软估计建模方法。在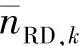服从高斯分布的前提假设下，维特比译码算法中，与x_k相关联的分支度量可表示为

类似地，对于MAP译码器，式（4.48a）中，γ_k（m，m′）中与x_k相关联的分支度量为

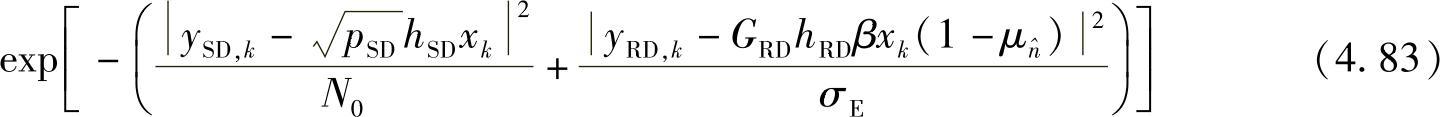
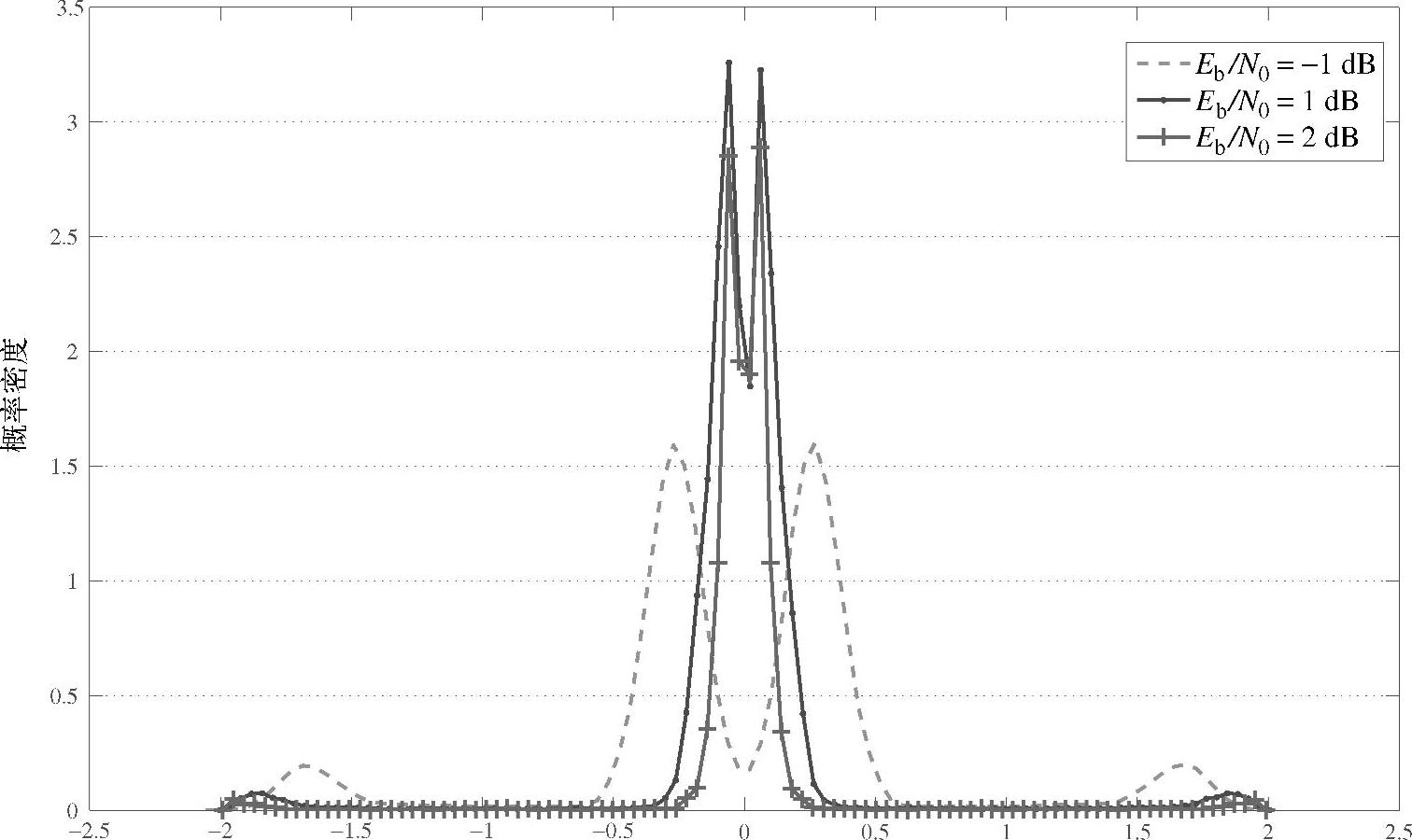
图4.6 中继处符号软估计的等效噪声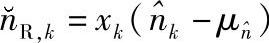的分布

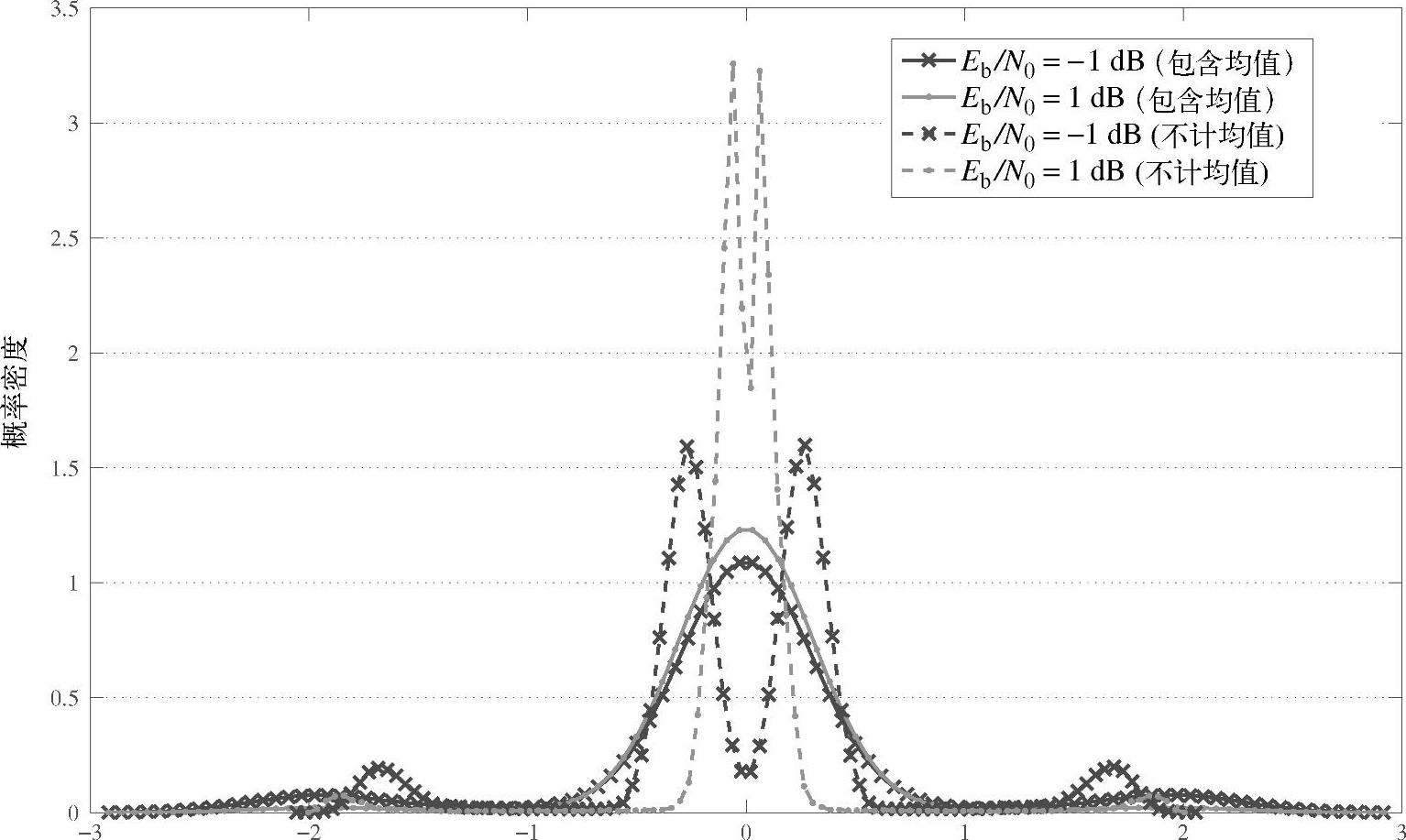
图4.7 中继处符号软估计的等效噪声和的分布对比图

应当指出的是，近似服从高斯分布的的方差实际上并不完全等于式（4.75）中两噪声项的方差之和。也就是说，式（4.76）计算的σ²_E实际上并不完全等于近似服从高斯分布的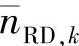的方差。这主要是因为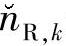并不严格服从高斯分布。为了修正近似服从高斯分布的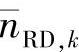的方差，将式（4.76）修正为

其中，L_v为方差修正系数。

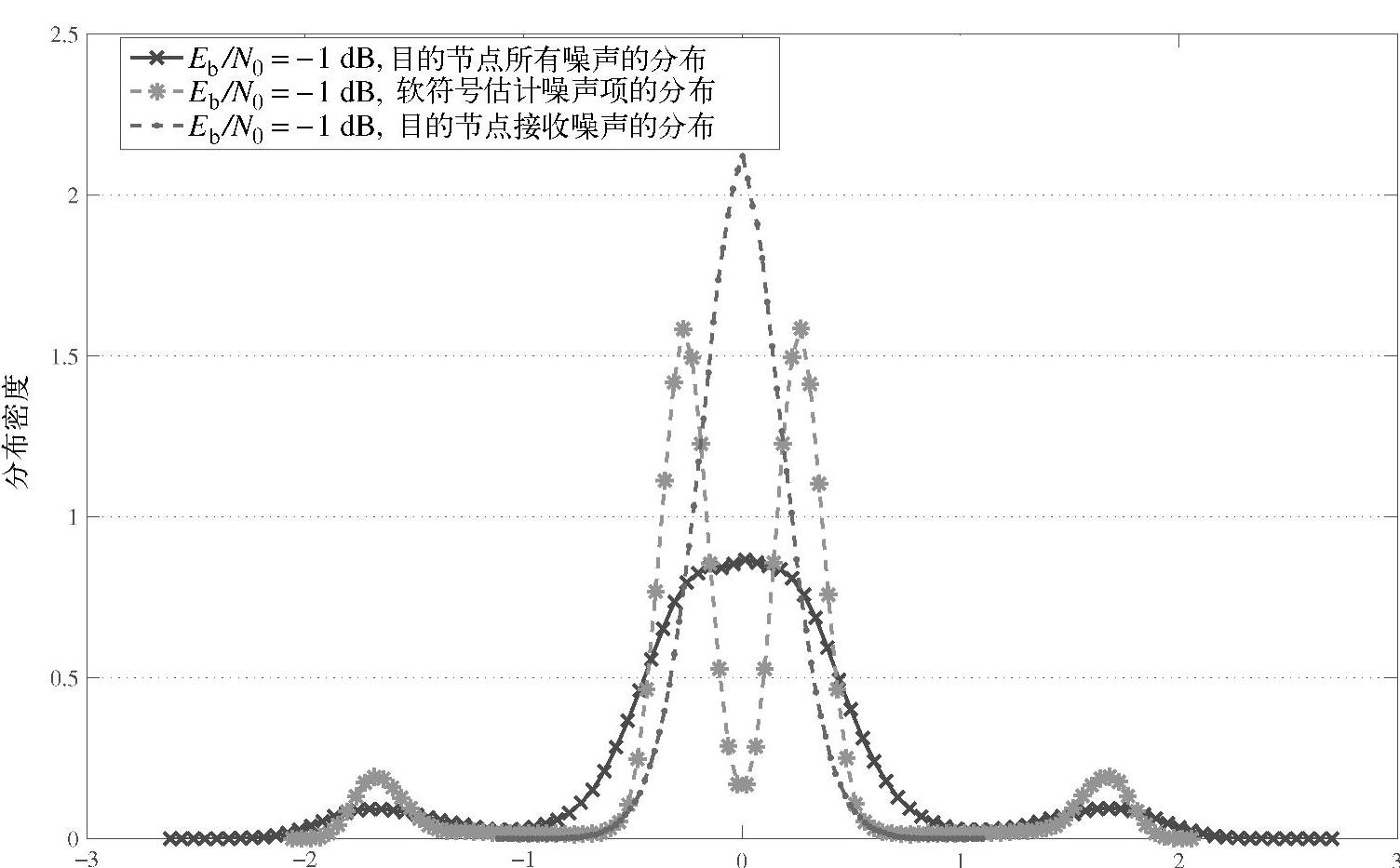
图4.8 当E_b/N₀=-1dB且n_RD，k的方差是ň_R，k的0.1倍时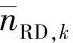，，ň_R，k和n_RD，k的分布对比图

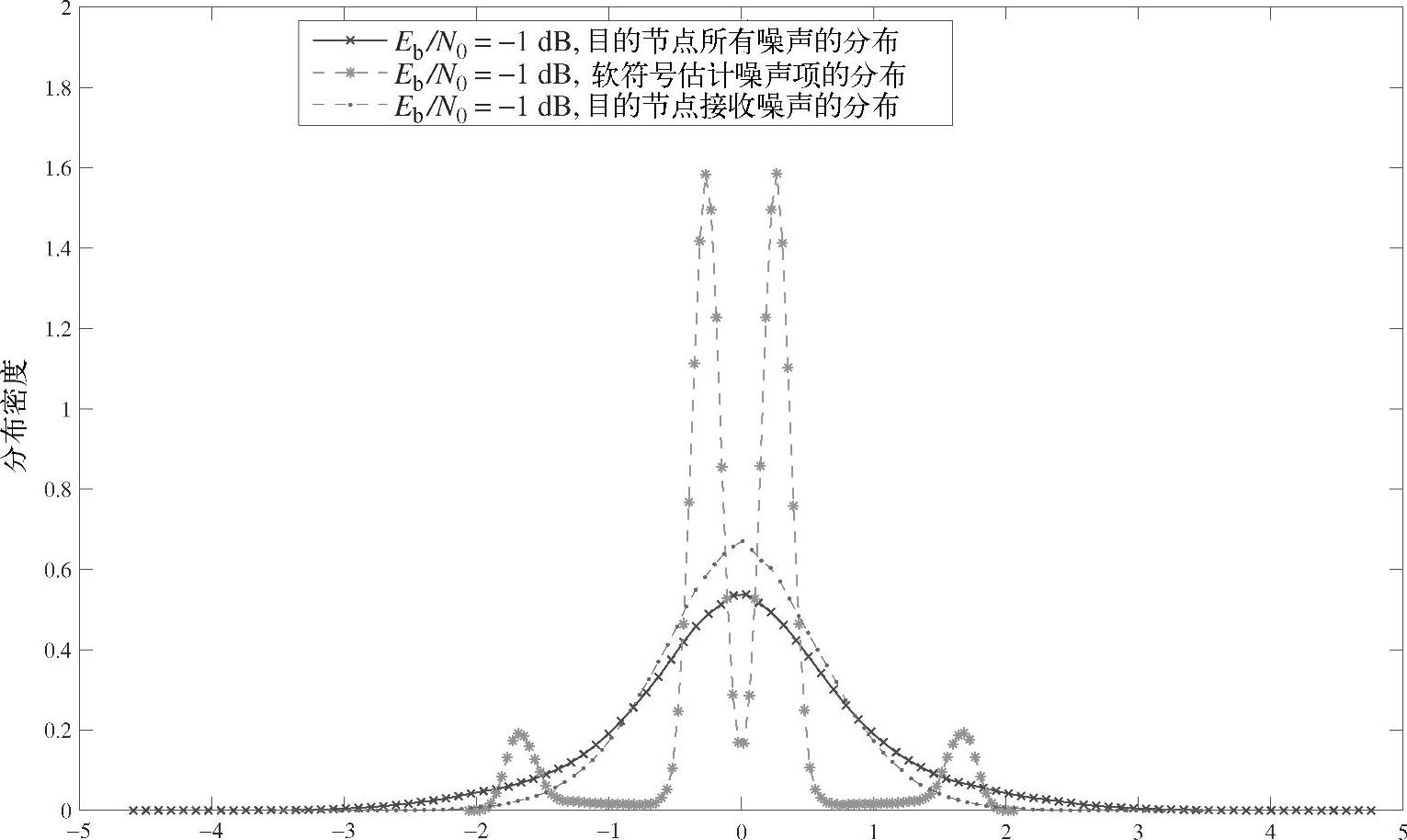
图4.9 当E_b/N₀=-1dB且n_RD，k与的方差相同时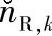，，和n_RD，k的分布对比图

当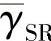分别等于0dB、5dB和10dB时，SIR-SSE相对于不同L_v值的BER性能如图4.10～图4.12所示，其中“R-DSNR”表示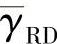。由图可知，当L_v值逐渐增加到2时，BER性能下降非常快；当2＜L_v＜8时，BER的性能几乎是不变的，且在这一取值区域内BER对L_v值的变化并不敏感，这对于选择最优的L_v值非常有利。因此可以在2＜L_v＜8的区间内选择Lv值而对性能没有影响。这也表明了当假定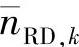服从近似高斯分布时，式（4.76）实际上低估了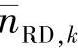的真实方差。为了获得令人满意的BER性能，L_v必须至少大于2。下面我们选择L_v=4作为默认的最优的L_v值。

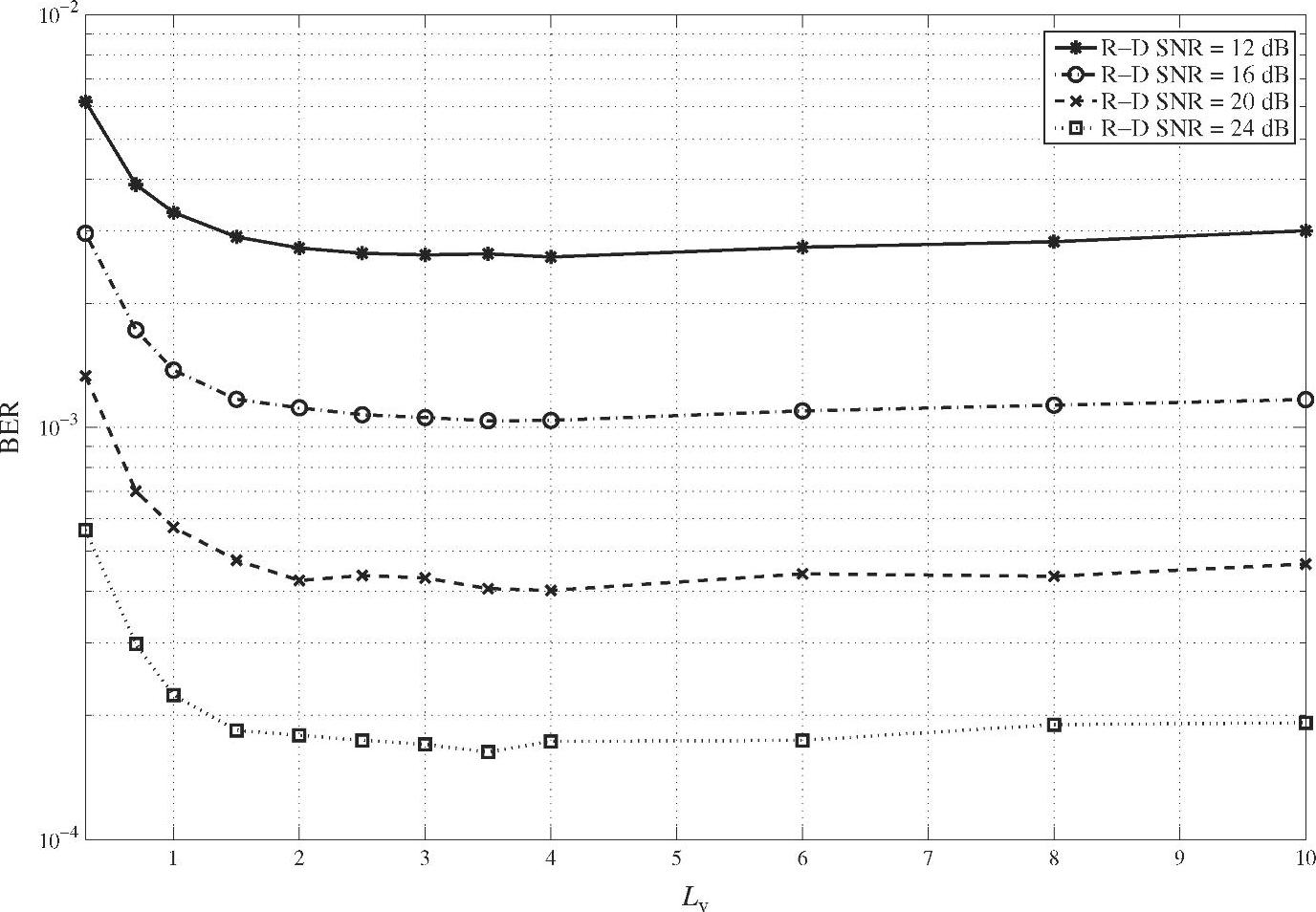
图4.10 当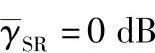时，不同修正系数下的BER性能

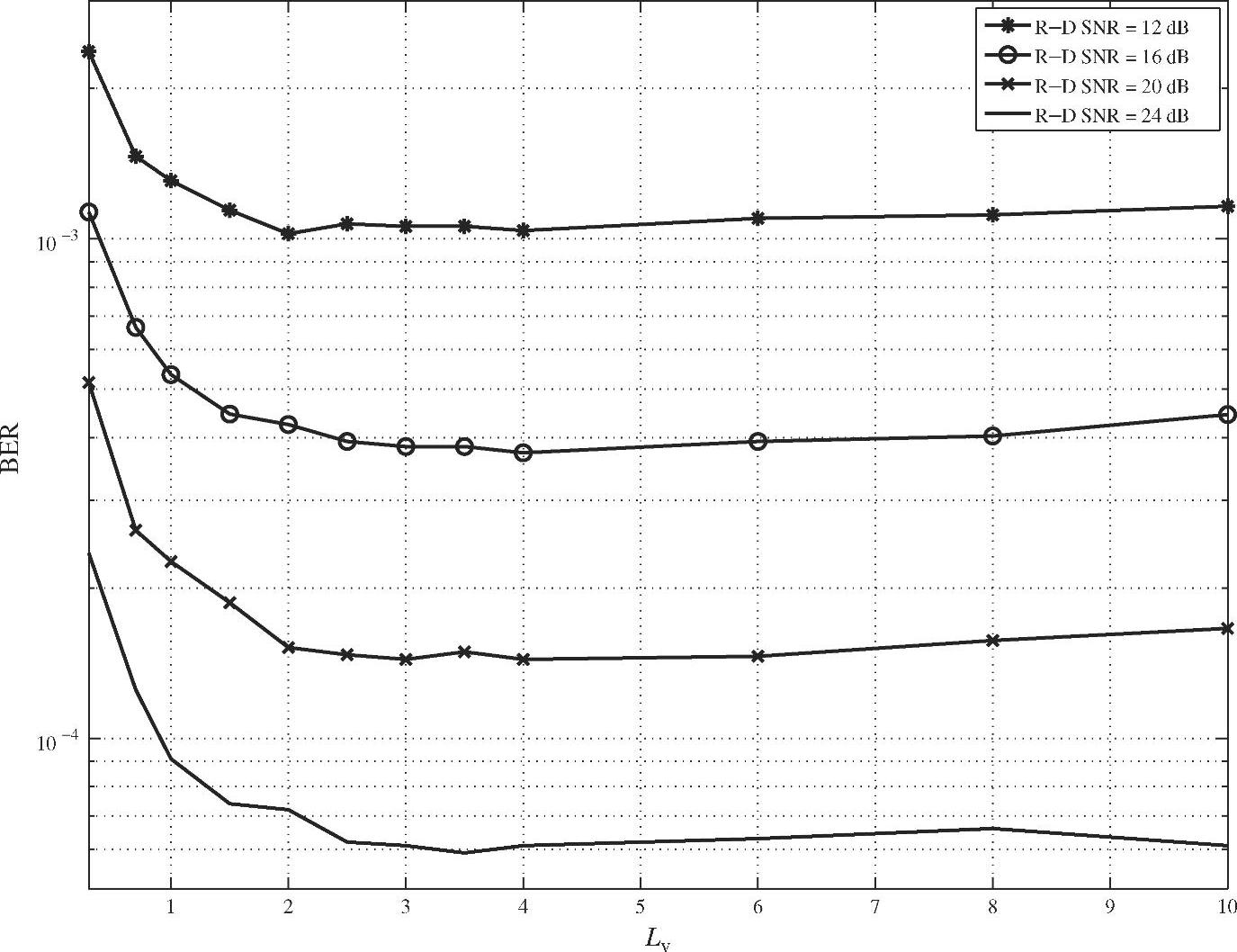
图4.11 当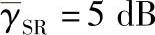时，不同修正系数下的BER性能

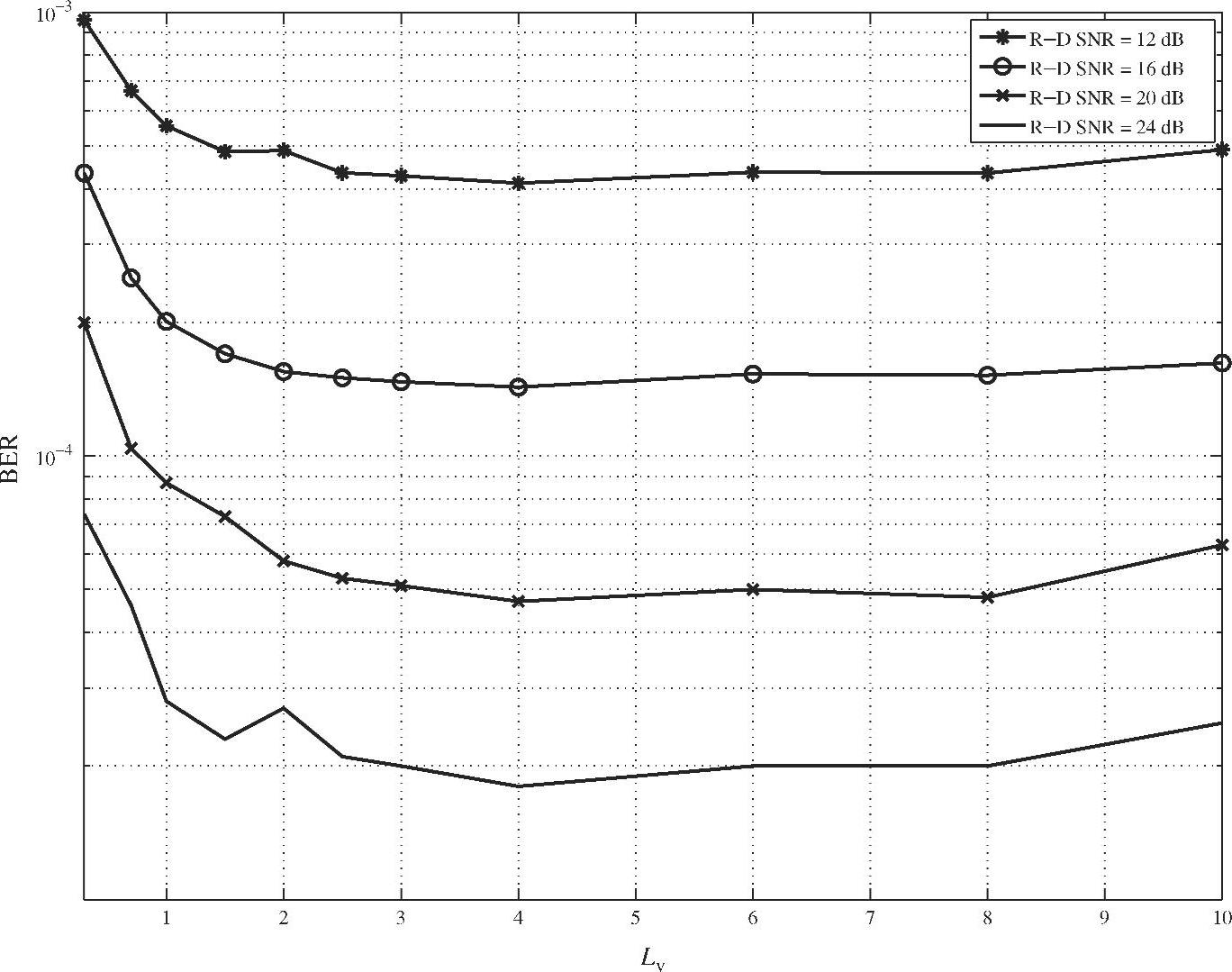
图4.12 当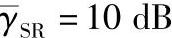时，不同修正系数下的BER性能

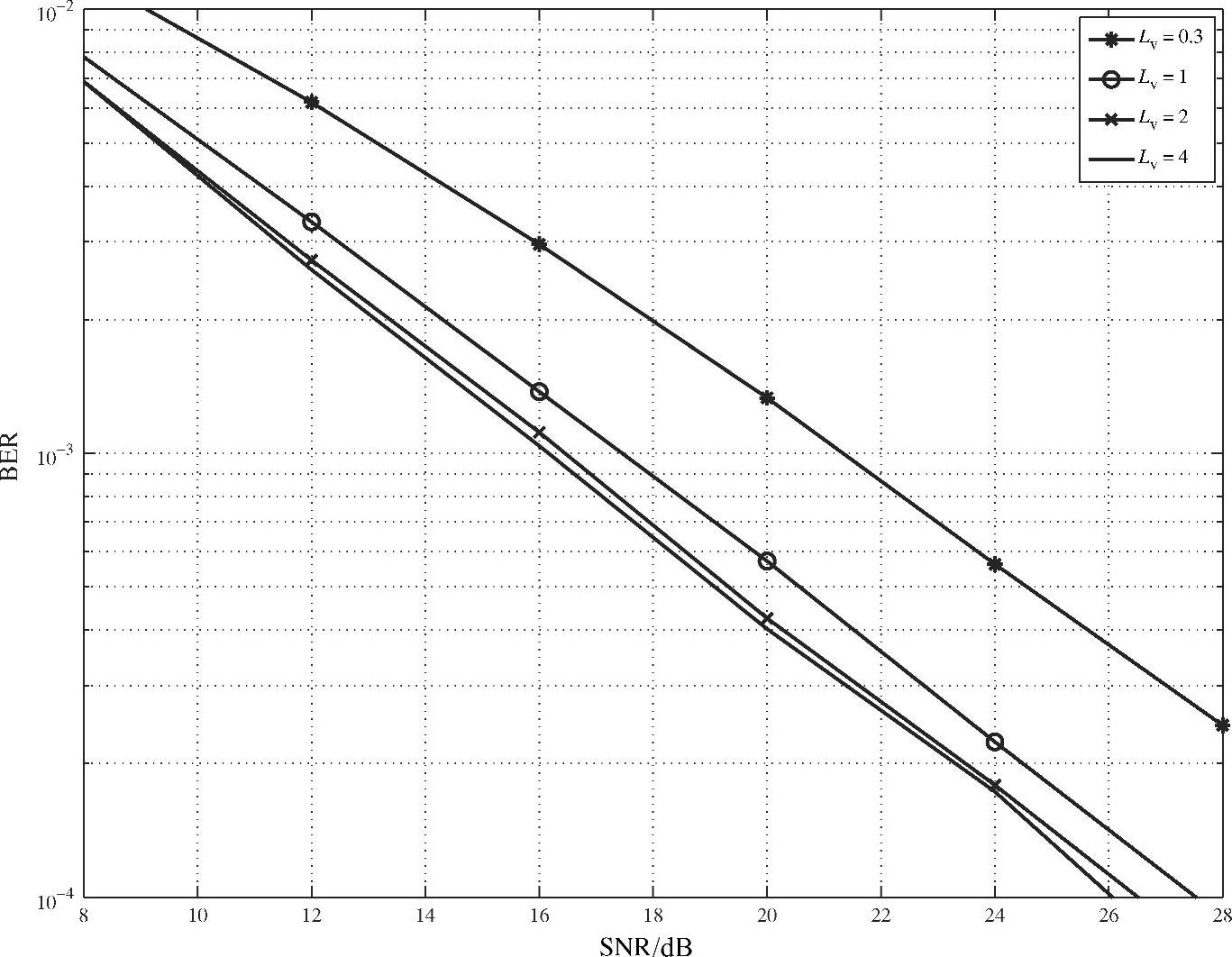
图4.13 当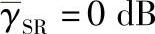时，不同修正系数下的BER性能

当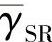分别等于0 dB、5 dB和10 dB时，图4.13～图4.15对比了SIR SSE中相对于不同L_v值的BER性能。由图可知，SIR-SSE取L_v=4的BER性能相比无方差修正，即L_v=1时要好1～2 dB，相比L_v=0.3要好得更多。此外，当L_v＜2时，译码器对方差非常敏感。如此不精确的方差估计会严重降低系统性能。但在SIR-SSE方案中获得的方差的精确解析解

图4.14 当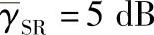时，不同修正系数下的BER性能

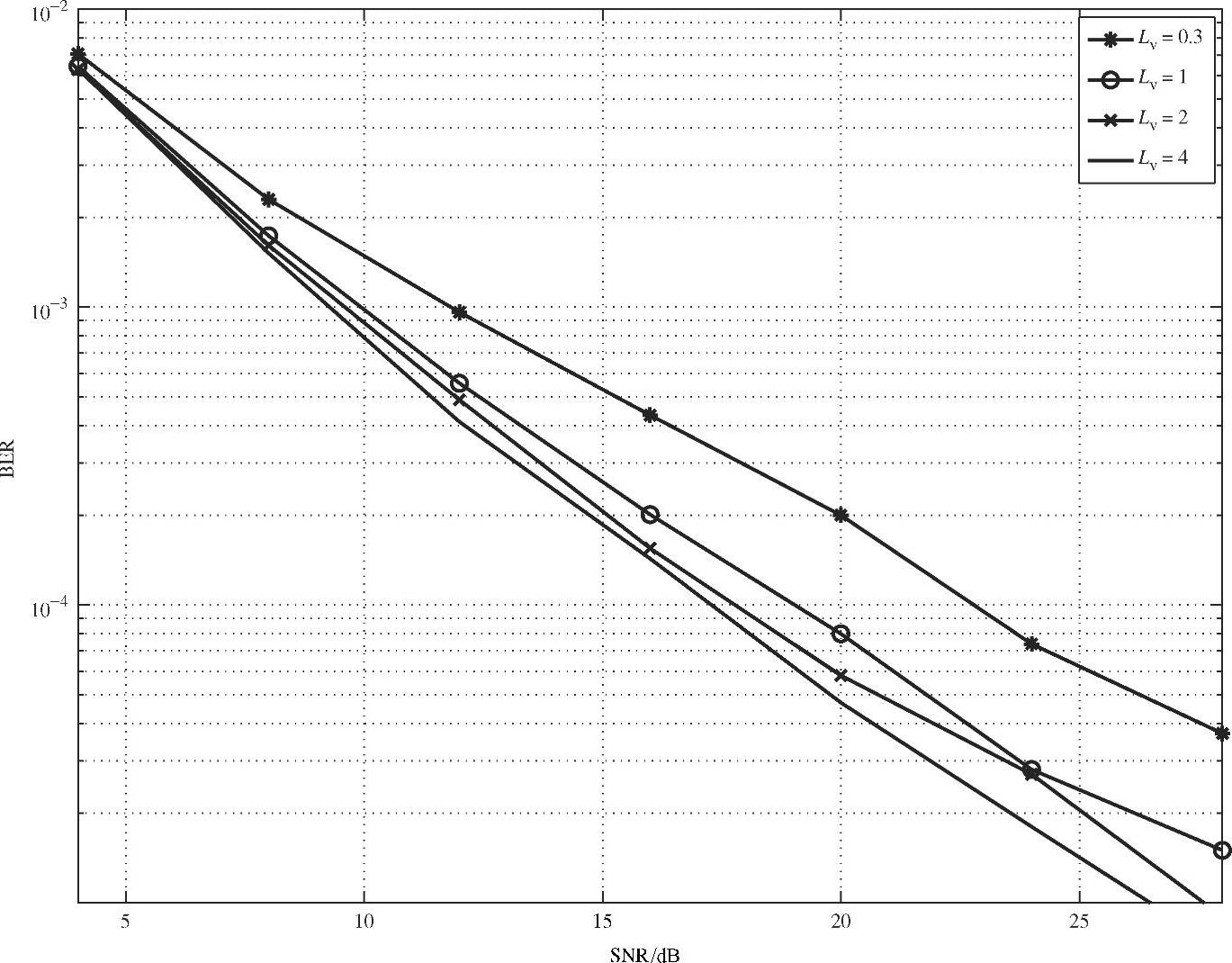
图4.15 当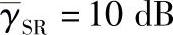时，不同修正系数下的BER性能

非常具有挑战性，是一个有待解决的问题。因此，我们主要依赖于仿真以获得最优的修正系数与方差估计值。另一方面，在2＜L_v＜8的区间内，SIR-SSE方案对L_v值的变化不敏感，使得选择最优的L_v值时有很大的自由性和灵活性。

4.2.3.2 基于对数似然比的SIR

本节介绍基于对数似然比的软信息表示方法（SIR-LLR）^{[455，457，458]}。与前面一样，考虑BPSK调制。令L_r（k）表示中继译码器的输出的LLR值：

令P_L为L_r（k）的平均功率，P_L可由下式计算：

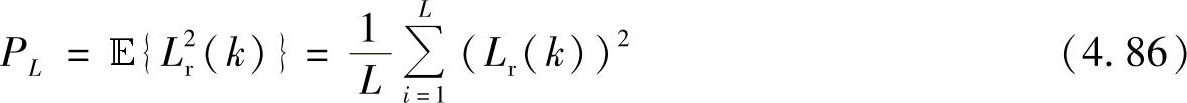
此外，令μ_L和σ²_L分别是L_r（k）的均值和方差（假定传输x_k=1），计算式为

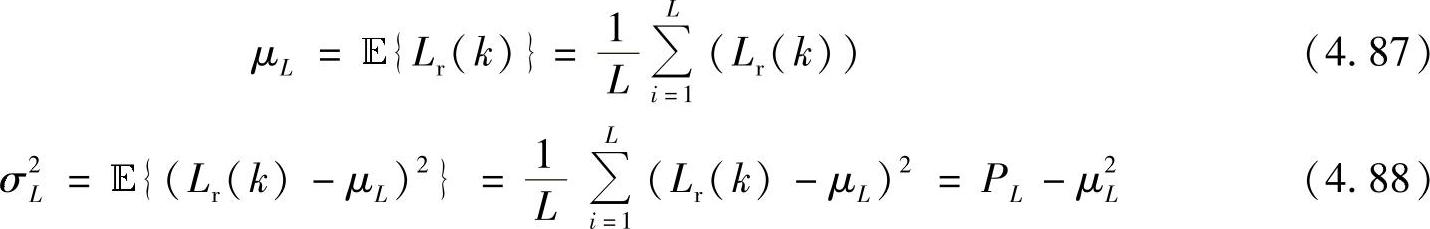
L_r（k）的统计分布受到了非常广泛的关注，众所周知，码字长度很长时LLR值服从近似高斯分布^[463]。现在我们假定信道编码的码字足够长从而使高斯分布近似成立，L_r（k）的概率密度函数（PDF）P_L（x）可以近似表示为

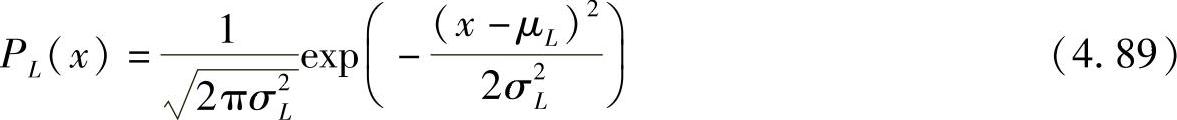
与上一节使用的模型类似，L_r（k）可以表示为[455，457]

其中，x_k是发送的真实符号；n_L，k是方差为σ²_L的等效噪声。图4.16示意了n_L，k的分布，其系统参数配置与图4.5相同。由图可知，在低SNR和高SNR时，n_L，k都服从近似高斯分布。需要指出的是，随着E_b/N₀的增加，PDF曲线的形状变得越来越窄。这说明n_L，k的方差也表征了等效噪声的平均功率随着E_b/N₀的增加而减小。

由式（4.90）可得

这与式（4.88）一致。因此，中继转发的信号可以表示为

其中，β是归一化系数，使得x_R，k满足中继发射功率限制pR

将式（4.91）和式（4.92）代入式（4.93）中，则β为

因此，目的节点的相应接收信号为

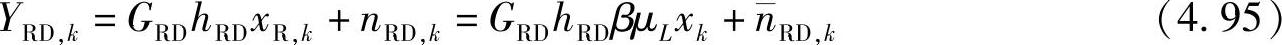
其中，为目的节点的等效噪声，其均值为零，方差σ²_E为

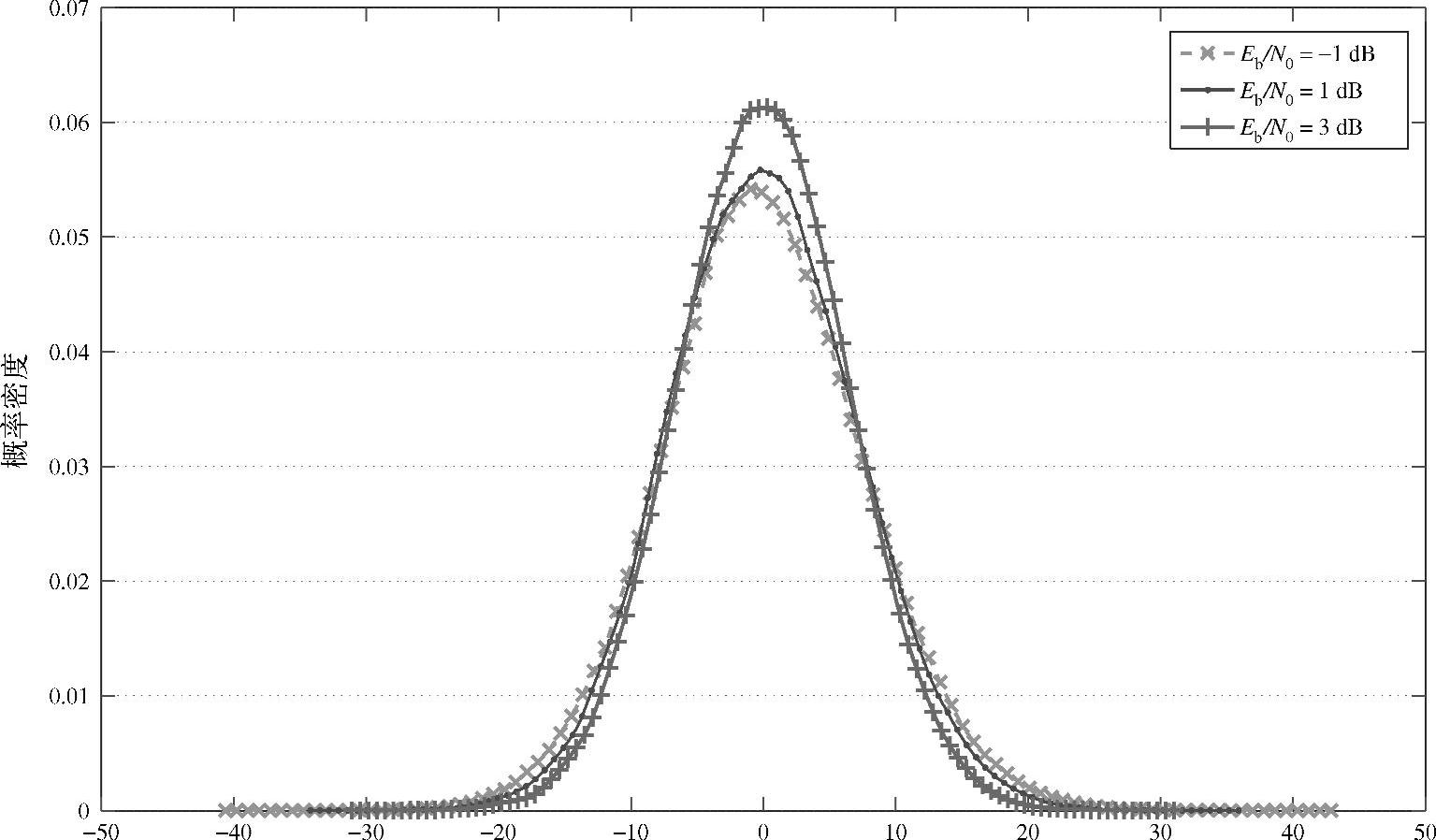
图4.16 中继处LLR形式的等效噪声n_L，k的分布

由于假定n_L，k服从高斯分布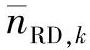，是两个高斯随机变量的线性组合且同样服从高斯分布。与SIR-SSE方法相似，在维特比译码过程中与x_k相关联的分支度量为

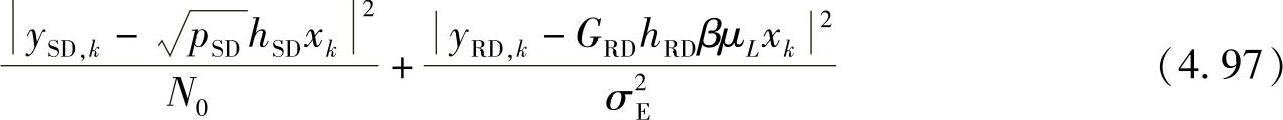
对于MAP译码，γ_k（m，m′）中与x_k相关联的分支度量最终可表示为

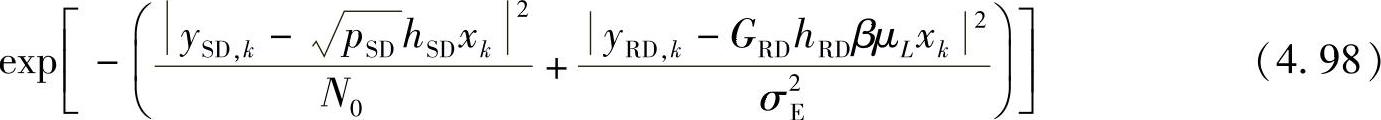
4.2.3.3 中继处信号估计的均方误差

本节首先比较几种中继转发协议中的中继处信号估计的均方误差（MSE）。令x_R，k为中继转发的信号，表示为

其中，β_r是放大系数；x_k是源节点的发送信号；n_r（k）是x_R，k的等效噪声。定义MSE为等效噪声项β_rn_r（k）的方差，即

为了简单起见，考虑AWGN信道和BPSK调制。源到中继链路使用码率为1/2、状态数为4、生成矩阵为（1，5/7）的RSC码。中继节点的接收噪声在每个维度上的方差为0.5，只需考虑接收信号的实数部分。比较AF、DF、EF、SIR-SSE和SIR-LLR这5种中继方案的MSE。其中，DF和EF的不同之处在于，采用DF协议的中继对接收信号进行译码，并对译码输出的信息符号和校验符号进行硬判决；而采用EF协议的中继只是解调接收信号而不译码。这些方案的MSE分别为

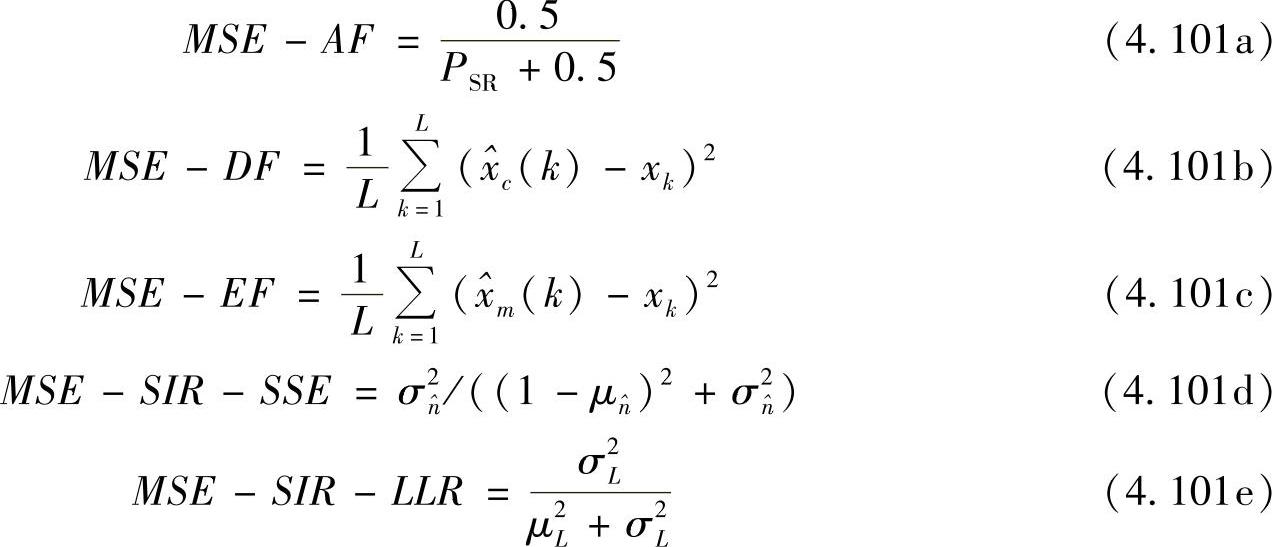
其中，式（4.101a）中的P_SR是中继的接收功率，噪声的实数部分的功率为0.5；式（4.101b）中的（k）是译码和硬判决后对x_k的估计值；式（4.101c）中的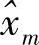（k）是解调符号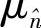；和是x_k的符号软估计中等效噪声的均值和方差；式（4.101e）中μ_L和σ_L是LLR值的均值和方差。

图4.17比较了各种中继方案中符号估计的MSE，x轴表示S-R链路的SNR。由图可知，在均方误差最小意义上，SIR-SSE最优，DF与SIR-SSE相近，而AF、EF和SIR-LLR的MSE很大。

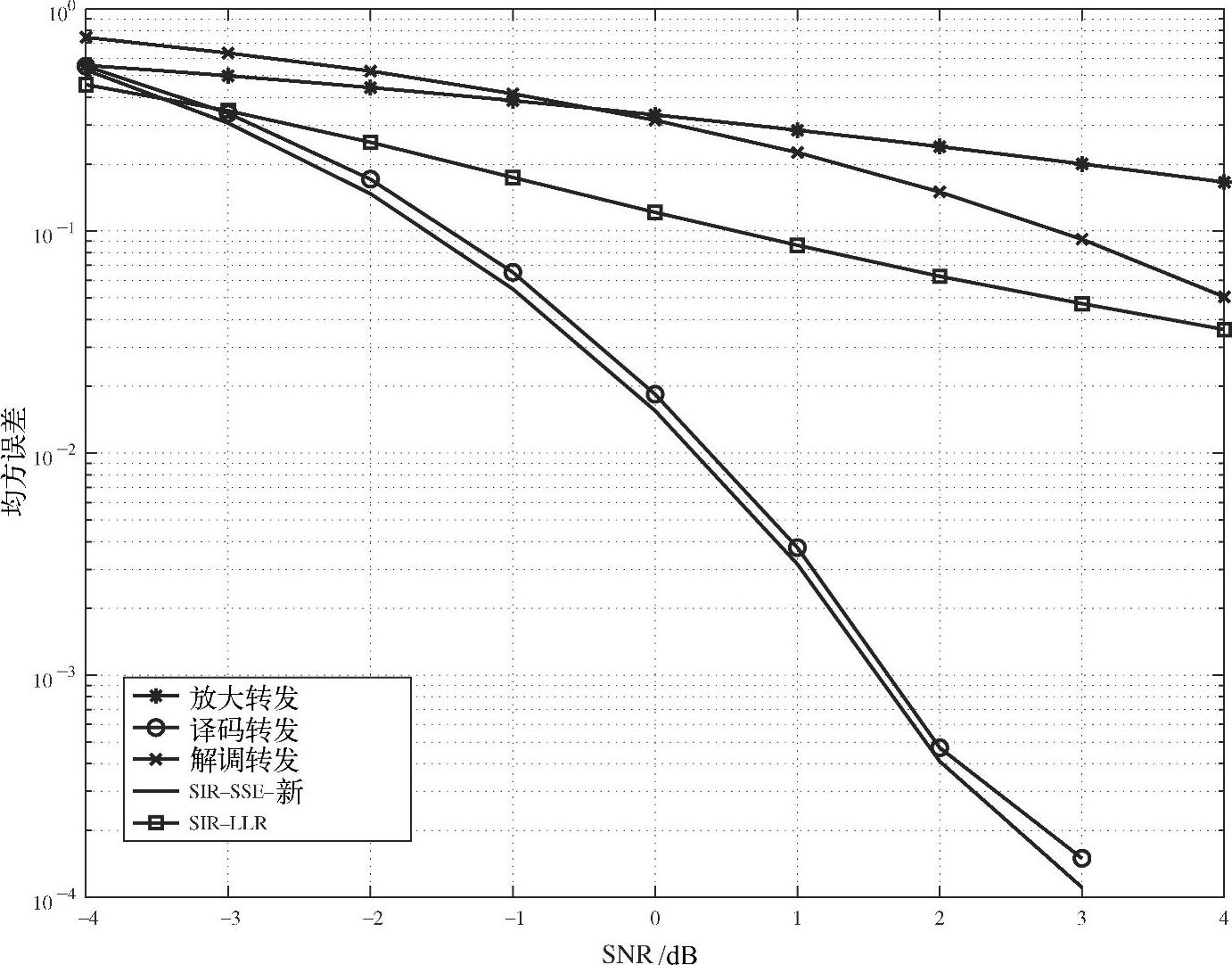
图4.17 不同中继转发方案中，中继处符号估计的均方误差

4.2.3.4 仿真结果

本节比较各种SIR方案的性能，所有仿真都基于BPSK调制，每帧包含130个符号，且信道服从准静态瑞利衰落。

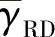为简单起见，假定S-D链路的平均信噪比等于R-D链路的平均信噪比γ。依然采用码率为1/2、状态数为4、生成矩阵为（1，5/7）的RSC编码方案。

这里分析SIR-SSE-新模型和SIR-SSE-传统模型两种方案，其中SIR-SSE-传统模型方案是指采用下式所示的传统软符号估计（SSE）建模方法的SIR-SSE方案：

其中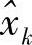，是中继译码器的SSE输出；x_k为期望的符号；为高斯随机变量。SIR-SSE-新模型方案是指4.2.3.1节采用的如下式所示的建模方法：

图4.18～图4.20是AF，SIR-SSE-传统模型，SIR-SSE-新模型和SIR-LLR方案的BER性能对比。图中x轴表示R-D链路的平均SNR。我们评估了两种SIR-SSE-新模型方案，一种没有方差修正系数，即L_v=1；另一种有方差修正系数，仿真中该值取4。

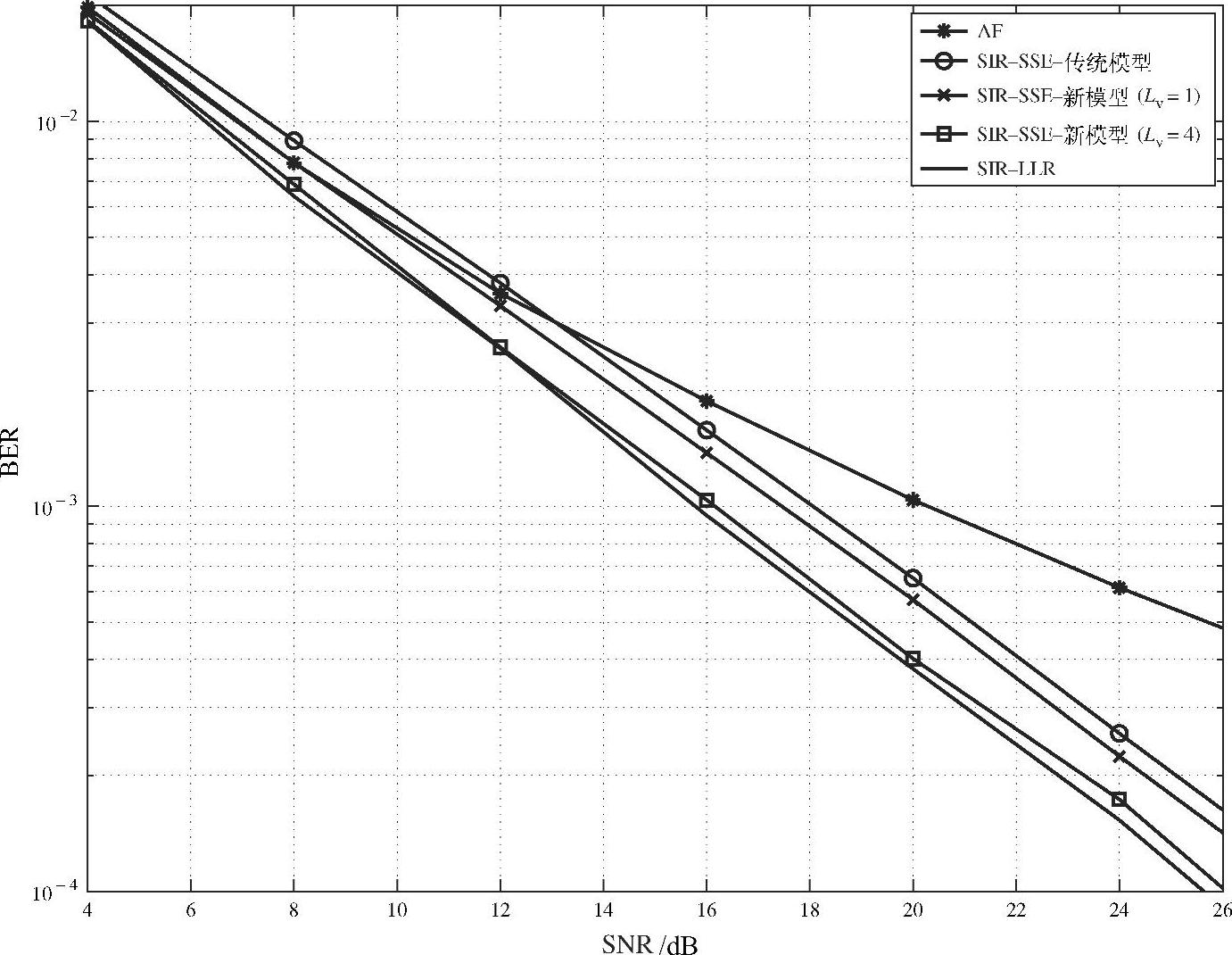
图4.18 当时，不同修正系数下的BER性能

由图可知，采用方差修正的SIR-SSE-新模型方案和SIR-LLR方案在整个SNR区间有几乎相同的性能，且明显优于其他SIR方案。例如，当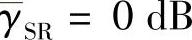、BER为10^-3时，相比于没有方差修正因子的SIR-SSE-新模型和SIR-SSE-传统模型，采用方差修正的方案分别有1.5dB和2dB的增益。所有SIR方案都显著优于AF方案，特别是在高信噪比时。例如，当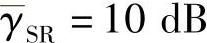、BER为10^-4时相比于AF方案，SIR-SSE-新模型（L_v=4）和SIR-SSE-传统模型（L_v=1）方案分别有5dB和3dB的增益，且增益随着的增加而进一步增大。由图还可以发现，SIR-SSE-新模型方案总是比采用传统软符号估计建模方法的SIR方案（即SIR-SSE-传统模型）的性能好，这也验证了4.2.3.1节中介绍的SIR-SSE-新模型方案采用的软符号估计建模方法的优越性。

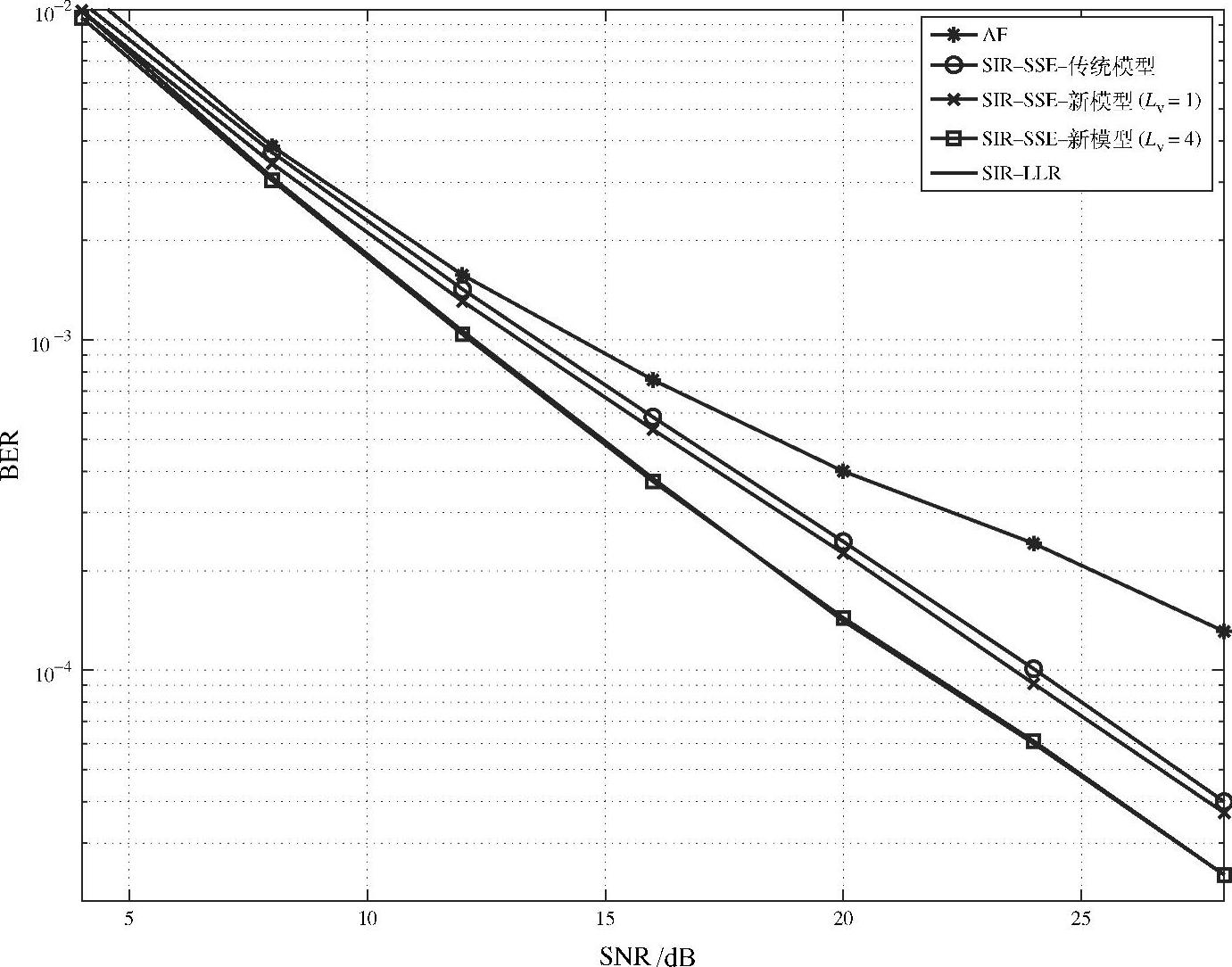
图4.19 当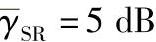时，不同修正系数下的BER性能

图4.20 当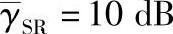时，不同修正系数下的BER性能

如果将图4.17和图4-18～图4-20进行对比，可以发现虽然SIR-SSE-新模型方案的MSE要小于SIR-LLR方案，但两者的BER性能却非常接近，其原因是我们假设SIR-SSE-新模型方案中符号软估计的等效噪声接近高斯分布，这种近似并不十分准确。如果采用更准确的分布，可能会进一步提升SIR-SSE-新模型方案的性能。如何找到并且用公式表示这种分布非常重要，也非常具有挑战性，遗憾的是该问题迄今为止还没有得到解决。

软信息是模拟信号，因而在实际系统中，为了传输模拟信号，中继应当采用压缩和量化或者其他调制技术。4.2.2节中的基于Wyner-Ziv编码（CF-WZC）压缩转发协议可以用来将模拟软信息量化为数字信号并且在发送之前压缩量化信号。因此，软信息转发可以与压缩转发方案联合起来作为实际系统中使用的单中继协议。此外，软信息也可以采用称为连续调制的模拟相位调制技术^[464]。除了这些方法之外，还存在其他可能的方法发送软信息。遗憾的是，在何种方式下发送软信息可以获得最优性能，仍然是一个开放课题。