压缩转发协议：提高传输效率的有效解决方案

无线中继网络中，中继与目的节点的接收信号是同一源信号由不同噪声加扰后的不同版本，因此两个版本的接收信号存在相关性，中继可以利用这种相关性压缩接收信号。利用这种相关性来压缩接收信号的中继协议称为压缩转发（CF）协议。CF协议中，中继通过量化、压缩并转发接收信号至目的节点。CF是另一种重要的再生中继协议，但其关注度远低于AF和DF协议。

CF的概念最初由Cover和Gamal提出^[96]。近来提出了一些实用的CF协议，包括基于量化转发的CF协议^[443，444]，基于Wyner-Ziv编码的CF协议（CF-WZC）以及基于Slepian-Wolf编码的CF协议（CF-SWC）^[448，449]。本节将主要介绍CF-WZC和CF-SWC协议。需注意的是，一些文献中也将CF称为量化转发或估计转发^[450]。广义上，放大、译码都可以视为估计方法，因而可将AF和DF视为CF的特殊情况。

4.2.2.1 基于Wyner-Ziv编码的CF协议

本节介绍基于Wyner-Ziv编码的CF方案^[451]。Wyner-Ziv编码器通常由量化器及其后续的索引编码器构成。量化器先将输入的模拟信号转换成数字信号，然后索引编码器对数字信号进行压缩处理。对于Wyner-Ziv编码，量化器的设计必须考虑索引编码器的类型。常用的索引编码器包括Slepian-Wolf编码、单源熵编码等。本节主要考虑量化器设计，而Slepian-Wolf编码将在下节考虑。为了简化起见，我们考虑由Hu和Li提出的固定比率标量量化器^[445]。

在量化之前，中继节点首先评估接收信号的可靠性以判定信号可否正确译码。实际系统通常将CRC比特添加到信息块上，根据CRC校验码可以很容易地判断译码成功与否。中继也可以通过测量接收信号的信噪比来简单估计译码的正确性。文献[452]的研究表明，对于给定的信道编码方案，存在一个由Bhattacharyya编码参数所确定的门限值，当接收信噪比大于此门限值时，接收信号能正确译码的概率随着码字长度趋于无穷而逐渐逼近于1。因此，中继可以简单地将接收信号的SNR与该门限值进行对比来估计译码的正确性。

如果中继能成功译码，则可采用DF协议，此时不需要量化处理；如果中继译码失败，则可采用CF协议。下面只考虑采用CF协议的情况。

令y_SR，k表示k时刻中继的接收信号。中继可以直接量化y_SR，k，也可以先对y_SR，k进行软译码，获得符号的软估计值或对数似然比（LLR）信息后再量化软信息。本节不介绍软信息的计算和建模方法。事实上存在一个独立的协议用来实现软信息的计算和转发，即软信息转发（SIR）协议，该协议将在4.2.3节单独讨论。这里我们只介绍量化器的设计方法，其输入的信号可以是中继的接收信号，也可以是中继处理后的信号，如软信息等。

令r_k表示量化器的输入信号。量化器将r_k量化为二进制序列Q_k=（q_k，1，…，q_k，M），即量化阶数为2^M。量化器的设计就是在一定的准则下确定最优的量化区间边界值B₀，…，B_i，…，B_2M。当B_i-1＜r_k＜B_i时，r_k被映射为二进制序列L_i，即

其中，Q（·）表示量化函数。我们以量化序列包含的信息最大为准则，这等价于在量化输出为Q_k的条件下，最小化信源符号x_k的熵，即

argminH（x_k|Q_k） （4.25）

其中，条件熵H（x_k|Q_k）为

且有

其中，p（r_kx_k）是发送x_k而接收到r_k的条件概率，且有

如在4.2.3节中将要介绍的，不论r_k是中继的接收信号还是译码软信息，都可以将其表示为

r_k=μ_rx_k+n_k （4.30）

其中，当r_k为接收信号时μ_r表示信道衰落系数，当r_k表示译码软信息时μ_r表示与软信息相关的标量（具体请参阅4.2.3节）；类似地，n_k表示等效噪声，即当r_k为接收信号时它表示接收噪声，当r_k为软信息时它表示软信息的估计误差。

无论r_k是哪种信号，假设n_k服从高斯分布，则p（r_kx_k）可以按下式计算：

其中，σ_r是n_k的均方差。假设r_k的概率密度p（r_k）基于原点对称，此假设在r_k为接收信号或软信息时成立。此时量化区间的边界值也是原点对称，即

其中，B₀=-∞且B_2M=∞。例如，在量化阶为4的量化器设计时[445]，量化区间的边界值分别是B₀、B₁、B₂、B₃、B₄。由式（4.32）可得(www.xing528.com)

此时只存在一个未知量B_d。将式（4.27）～式（4.31）代入式（4.26），则H（x_kQ_k）可以表示为B_d的函数，即G（B_d）。此时式（4.25）的最优化问题可以改写为

通过求解如下方程可获得最小值：

由于很难获得上述方程的闭式解，实际中通过数值计算求解。

找到最优的量化器之后，r_k被量化为Q_k并经调制后转发至目的节点。令y_RD，k为目的节点的接收信号。为了估计源节点发送的符号x_k，目的节点的接收机需要计算x_k的后验概率。假定采用最大后验概率（MAP）译码（参考4.2.3节中MAP译码器的介绍），其中与x_k有关的分支度量γ_k（m，m′）按下式进行修正：

其中，m和m′是编码格图中与x_k相关联的一对状态，y_SD，k、p_SD和h_SD分别为直传链路的接收信号、源节点发送功率以及源到目的节点链路的衰落系数。p（y_RD，k|x_k）可以借助于马尔可夫链x_k→r_k→Q_k→y_RD，k的性质计算获得，有

其中，p（Q_k，x_k）可通过式（4.28a）计算。p（y_RD，k|Q_k）依赖于Q_k的调制方式。如果向量Q_k被调制成单个符号S_k，且E（S_k²）=1，那么y_RD，k变成y_RD，k且p（y_RD，k|Q_k）为

其中，p_r、G_RD和h_SD分别表示中继发射功率、中继到目的节点链路的信道增益和衰落系数。如果Q_k=（q_k，1，…，q_k，M）中的每个比特q_k，i都被调制成一个符号s_k，i，则

其中，y_RD，k，i是与s_k，i相对应的接收信号，且有

4.2.2.2 基于Slepian-Wolf编码的CF协议

本节介绍基于Slepian-Wolf编码的CF协议（CF-SWC）^[453]。Slepian-Wolf编码用于处理两个或两个以上相关数据流的压缩过程。例如，两个相关的源节点X和Y，如果X以速率H（X）传输，利用Slepian-Wolf编码可以将Y压缩至速率H（YX）。目的节点可以通过对X和H（YX）进行联合译码而恢复X和Y。类似地，对于中继信道，中继接收的信号是源节点的发送信号经噪声加扰后的版本，因此可以利用Slepian-Wolf编码进行压缩。中继可以独立使用CF-SWC对二进制序列进行压缩，该序列可通过对中继接收信号进行硬判决获得^[448]。CF-SWC也可以和4.2.2节介绍的量化转发协议一同使用实现量化数字信号的压缩，从而构成基于Wyner-Ziv的CF协议^[443，447]。本节中只关注CF-SWC且假定Slepian-Wolf编码器的输入已是二进制序列，该序列或是对接收信号直接硬判获得，或是量化器的输出。

令B_R为Slepian-Wolf编码器的输入。CF-SWC协议的一个关键点就是码字分组处理，即将输入序列B_R分成若干组，每个分组都通过一个索引号进行标识。压缩过程就是将输入序列映射到索引号的过程，解压缩过程就是利用索引号来识别目标分组，并利用来自源节点的相关序列找出与该分组对应的序列。本节介绍一种常用的分组方法，即利用线性分组码的陪集构造分组。通过将属于G₂ⁿ的n维二进制序列x与线性分组码（n，k）码字集合相加获得陪集，其中G₂ⁿ是n维二进制空间。例如，给定一个线性分组码（n，k），码字集合C∈G₂ⁿ且随机向量x属于G₂ⁿ，下式所示的子集

x+C=x+c，c∈C （4.41）

构成C的一个陪集，用x+C表示。需注意的是，陪集通常不是子空间，且每个n维非零二进制序列z∈G₂ⁿ只属于一个陪集。

（n，k）分组码的码字集合C∈G₂ⁿ由2^k个码字组成，可以将G₂ⁿ划分成2ⁿ/2^k=2^n-k个互不重叠的陪集。因此，我们可以利用n-k长的二进制序列作为分组的索引号。令H表示（n，k）分组码集合C的校验矩阵。由编码理论可知，对于码字c∈C有cH^T=0。因此，对属于陪集x+C的任意向量y，有

其中，s=xH^T称为y的伴随式（校验子），它是n-k维的二进制序列。

由式（4.42）可知，属于相同陪集x+C的所有序列都具有相同的伴随式s=xH^T。因此，每个分组x+C同样也是C的一个陪集，可以利用伴随式s=xH^T作为索引号。按这种方式，索引号即该分组码字序列的伴随式，它唯一地标识了每个分组。因此，将n维二进制序列z∈G₂ⁿ压缩为对应的n-k维伴随式，压缩比为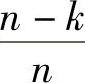。基于伴随式的码字分组是实现Sl-epian-Wolf压缩的一种方法。其他实现方法，在此不做讨论。

SWC编码器将长度为n的二进制输入序列B_R压缩为长度为n-k的分组索引s，对s进行调制后转发到目的节点。在目的节点，对存在相关性的来自中继的压缩信号和来自源节点的未压缩信号进行联合译码，可以恢复源节点发送的原始二进制信息序列。