传统DF协议和选择式译码转发协议的比较及线性复杂度的译码算法介绍

本节我们研究常用的译码转发（DF）再生中继协议。大部分分布式编码方案都基于DF协议。传统的DF协议中，中继对接收信号进行译码，无论译码正确与否，要么直接转发译码信息，要么对译码信息进行重编码后再转发。中继也可以仅转发能正确译码的译码信息，这就是将在4.2.5节中讨论的选择式译码转发（S-DF）协议，而在本节中只讨论传统的DF协议。本节首先给出系统模型，然后介绍源-中继-目的节点的中继链路的等效单跳信道模型，并介绍在文献[422]中提出的近似最优的合并技术，最后通过仿真对比多种中继方案以验证DF的性能。

4.2.1.1 系统模型

考虑由一个源节点、一个中继和一个目的节点构成的简单的两跳中继网络。为简单起见，考虑BPSK调制和无编码系统。

DF的传输过程可分为两步。首先源节点发送调制信号x_k至中继与目的节点，中继与目的节点处相应的接收信号分别为

其中，p_SR与p_SD分别为中继和目的节点处的接收信号功率；h_SR与h_SD分别为源至中继链路以及源至目的节点链路的信道衰落因子，它们都是零均值、相互独立的复高斯随机变量。我们考虑准静态衰落信道，即信道衰落值在一帧时间内固定不变，但在帧间独立变化。此外，n_SR，k与n_SD，k为零均值、双边功率谱密度为N₀/2的高斯随机噪声。

在未编码DF协议中，接收到来自源节点的信号后，中继采用最大似然检测（ML）算法估计x_k：

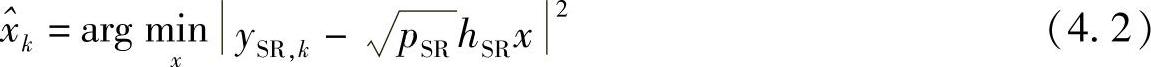
其中，是中继对x_k的估计值。随后中继以发射功率P_R转发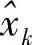至目的节点，目的节点处相应的接收信号为

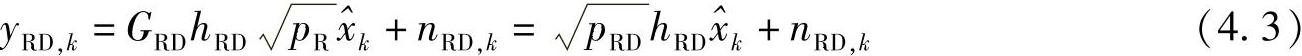
其中，p_RD=p_RG²_RD，G_RD，h_RD分别表示是中继至目的节点链路的信道增益和衰落因子，n_RD，k是目的节点处的接收噪声。

接收到分别来自源节点与中继的信号y_SD，k与y_RD，k后，目的节点对其进行联合处理以估计x_k。最佳的译码器采用ML译码算法实现译码误差最小化，即选择使似然函数p（y_SD，k，y_RD，k|x）最大的发送符号x作为译码输出

由于y_SD，k与y_RD，k相互独立，式（4.4）可表示为

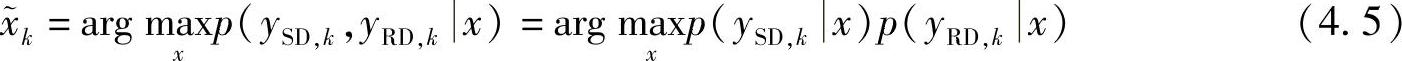
其中，p（y_SD，k|x）的表达式是

由于中继处可能存在译码错误，因此p（y_RD，k|x）的计算式与式（4.6）不同。假设PSR（γ_SR）是源到中继链路上x_k的误判概率，其中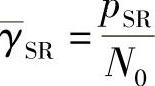，。可得

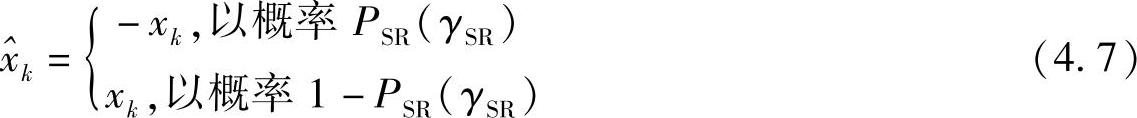
式中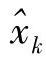，是中继对x_k的估计值。从式（4.7）可计算p（y_RD，k|x）为

将式（4.6）和（4.8）代入式（4.5），则最大似然译码估计值可表示为

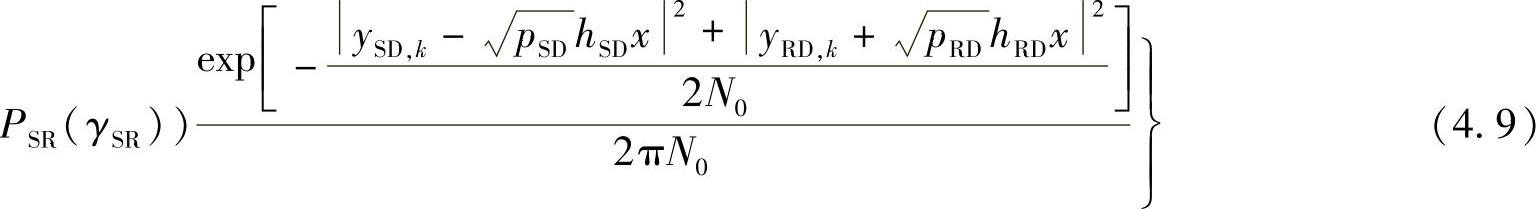
由式（4.9）可见，接收端采用ML译码算法的计算复杂很高，因为必须计算源到中继链路的错误率P_SR（γ_SR）。随后的4.2.1.2节中，我们引入具有线性复杂度的译码算法^[442]。

4.2.1.2 S-R-D链路的等效模型

在4.2.1.1节我们注意到ML译码算法相当复杂，本节将介绍一种简单的合并方式，其性能接近ML方法。我们知道最大比合并（MRC）是最优的且具有线性复杂度的合并技术。在DF中继系统中，为了减少目的节点的ML译码复杂度，应用MRC的思想将接收信号y_SD，k与y_RD，k合并为

y_D，k=w_SDy_SD，k+w_RDy_RD，k （4.10）

相应的符号估计为

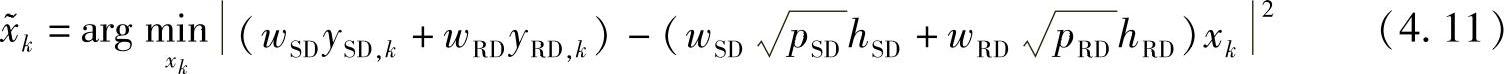
式中，w_SD和w_RD为合并因子，其值分别为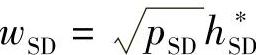与。当中继译码正确时，上述合并权重为最优。但对于实际的中继系统而言，当中继处存在译码误差时，上述合并权重远非最优，此时如何寻找最优的权重是一项颇具挑战性的任务。为了简化最优化问题，在文献[442]中提到用具有相同误比特概率的等效单跳链路代替S-R-D两跳链路。基于此等效单跳链路，我们设计DF协议的最优合并策略。

令γ_eq表示S-R-D链路的等效瞬时SNR，目的节点接收到的经由S-R-D链路的信号为(www.xing528.com)

其中，α_E＞1表示考虑中继的检测误差时的噪声功率放大系数；是目的节点的等效接收噪声，其双边带功率谱密度是N₀/2。由式（4.12）可计算等效的瞬时信噪比γ_eq：

由上式可得

其中，，。S-R-D链路的等效模型如图4.2所示。利用上述单跳等效模型，式（4.10）可以改写为

为使合并后的SNR最大，最优权重为

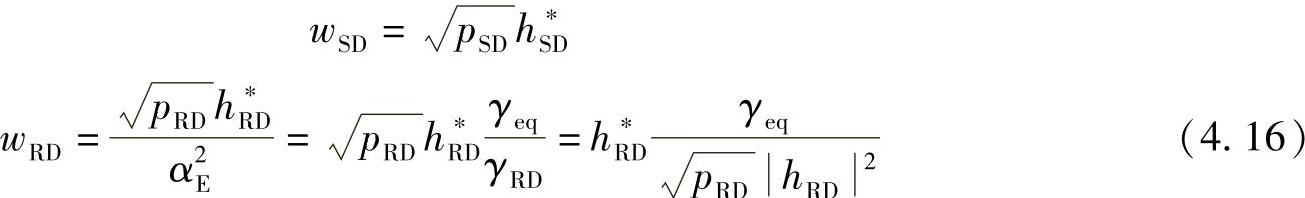
式（4.16）所示的最佳权重因子考虑了中继检测误差。上述基于等效单跳链路的MRC合并技术被称为协同MRC（C-MRC）^[442]。

目的节点处信号合并后的SNR为

其中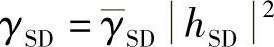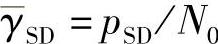，，。考虑到中继的检测错误，式（4.11）所示的判决度量需修正为

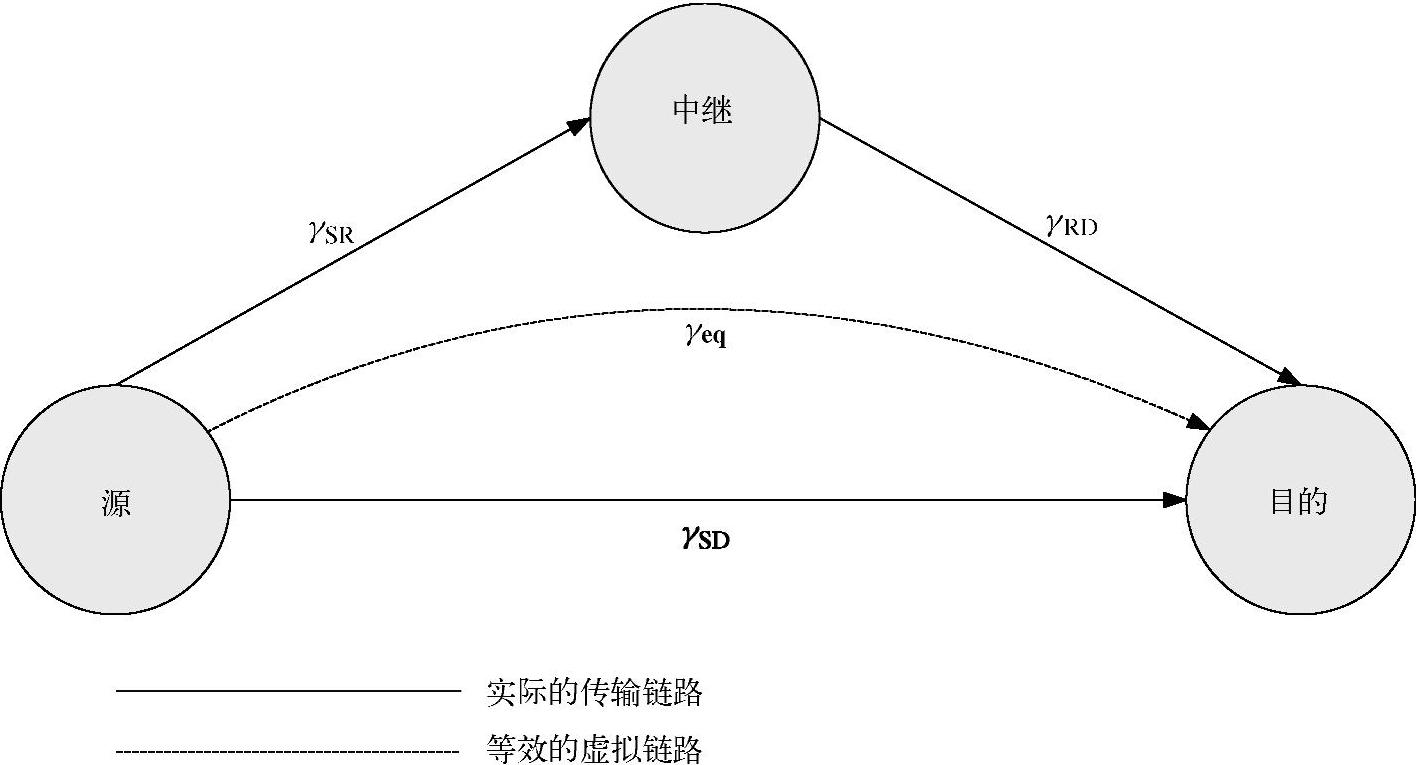
图4.2 DF中继协议中，S-R-D双跳链路的等效单跳链路系统模型

从上式可见，当γ_eq已知时，目的端可以利用等效单跳模型来简化DF译码。

接下来我们计算等效单跳链路的输出信噪比γ_eq。假设P_SRD（γ_SR，γ_RDh_SR，h_RD）为S-R-D链路的条件BEP，P_SR（γ_SRh_SR）和P_RD（γ_RDh_RD）分别表示源至中继链路和中继至目的节点链路的条件BEP。注意到在BPSK调制方案下，目的节点在下述两种情况下会判错：一种是S-R链路译码正确，但R-D链路译码出错；另外一种是S-R链路译码出错，而R-D链路译码正确。因而S-R-D两跳链路的总的条件BEP可以表示为

等效的单跳链路的输出SNR为

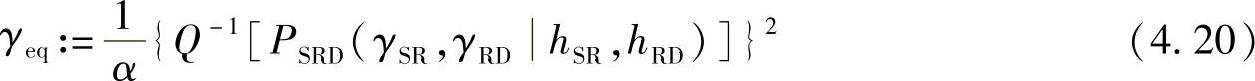
式中，Q（x）是Q函数，Q^-1（x）是Q（x）的反函数；α是由信号星座图决定的常数，例如，BPSK调制时α=2。定义γ_min：=min{γ_RD，γ_SR}，在文献[442]中已经证明，γ_min与γ_eq间的关系为

从上式可见，高信噪比时γ_min是γ_eq的很好的近似，因为此时3.24/α相比于γ_min是很小的，因而可以忽略即有

γ_eq≈γ_min （4.22）

因此在DF协议中，可以用γ_min来近似S-R-D链路的总信噪比。这种近似可以大大降低目的节点处的译码器复杂度。

4.2.1.3 仿真结果

本节评估采用协同MRC（CMRC）方案的DF协议性能，并与AF协议进行比较。仿真系统采用非编码的BPSK调制，帧长为100个符号，信道为准平稳衰落信道。仿真时考虑三种场景，即中继位于源节点与目的节点的中间位置处，中继更靠近源节点位置处，中继更靠近目的节点位置处。设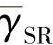、、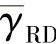分别表示S-R、R-D、S-D链路的平均输出信噪比。为了方便地在不同场景下评估系统性能，采用如下形式的SNR表示：

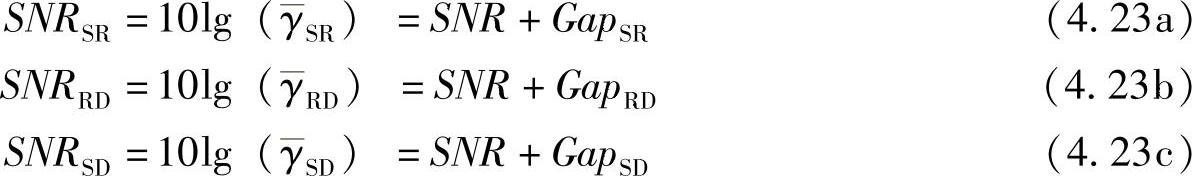
图4.3给出了采用C-MRC的DF方案在三种场景下的性能。三种场景下的输出信噪比分别为：（Gap_SR，Gap_RD，Gap_SD）=（0，0，0），（Gap_SR，Gap_RD，Gap_SD）=（0，30，0），以及（Gap_SR，Gap_RD，Gap_SD）=（30，0，0），所有数字都以dB为单位。从仿真曲线可以看出，场景1的系统性能最差，这是因为S-R与R-D链路的信噪比都很低；场景3时（Gap_SR，Gap_RD，Gap_SD）=（30，0，0）的系统性能最好，因为S-R链路的信噪比最大，从而中继处产生的错误传播概率最小。从图中还可看出采用C-MRC的DF方案性能比AF略差，但是两种方案均获得了分集度为2的满分集。

图4.3 C-MRC下的DF与AF性能的比较