前面章节主要针对透明中继下所有中继都参与转发处理的情况,其中一些中继在的正交的信道中进行传输。尽管信道的正交性假设降低了系统复杂度,但同时也限制了系统吞吐量。一些透明中继协议放松了信道正交性的限制,例如分布式波束赋型。这虽然可以提高系统容量,但由于目的节点需要反馈大量信息给中继从而带来更高的处理复杂度,例如需要反馈一些通用参数和各中继到目的节点的CSI。为了解决上述问题,本节中提出一种基于AF转发协议的中继选择算法,以简化非正交两跳多中继系统的设计。相比所有中继都参与的正交AF方案,这种中继选择算法可以有效提高系统性能和容量。
3.4.2.1 系统模型
考虑3.3.4节所述的两跳系统模型,包括一个源节点、n个中继节点和一个目的节点,且无直传链路。令hiSR和hiRD(i=1,…,n)分别表示源节点到第i个中继和第i个中继到目的节点的信道衰落值,GiSR和GiRD(i=1,…,n)分别表示源节点到第i个中继和第i个中继到目的节点的信道增益(即路损)。假设hiSR和hiRD的方差相同且为1。信道是准平稳衰落信道,其模值服从瑞利分布。令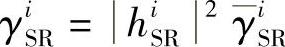 和
和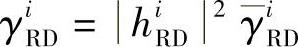 分别表示源节点到第i个中继和第i个中继到目的节点的瞬时接收SNR,其中
分别表示源节点到第i个中继和第i个中继到目的节点的瞬时接收SNR,其中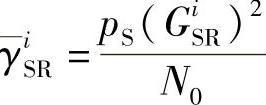 ,
,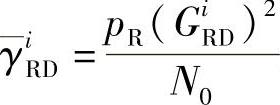 分别表示源节点到第i个中继和第i个中继到目的节点的平均SNR,pS指源节点的发射功率、pR指中继节点的发射功率。为了简化起见,假设
分别表示源节点到第i个中继和第i个中继到目的节点的平均SNR,pS指源节点的发射功率、pR指中继节点的发射功率。为了简化起见,假设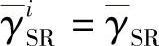 ,
,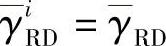 ,i=1,…,n。令Li表示从源节点经历中继i到目的节点的全部链路,即第i条中继链路,γiSRD为第i条中继链路的接收SNR,与AF系统中的计算相同,可以表示为
,i=1,…,n。令Li表示从源节点经历中继i到目的节点的全部链路,即第i条中继链路,γiSRD为第i条中继链路的接收SNR,与AF系统中的计算相同,可以表示为

AF中继选择策略是在所有中继节点中选择γiSRD最大的中继转发信息,而其他中继节点保持空闲状态。从所有中继中选择一个中继节点S由下式决定:

S表示n条中继链路中信道质量最好的。与Bletsas等人在文献[437]中讨论的相似,为了实现中继选择策略,每个中继节点分别从源节点和目的节点接收请求-发送(RTS)和清除-发送(CTS)信号。基于此接收信号,每个中继节点估计它到源节点和目的节点的信道增益。然后使用回退(back-off)计时器设定一个与γiSRD成反比的数值,其中具有最大γiSRD值和最小回退计时器值的中继节点将占用传输信道。通过这种方式实现了分布式的中继选择,而每个中继只需根据来自源节点的RTS信号和来自目的节点的CTS信号就可估计信道幅值。
3.4.2.2 性能分析
本节中,我们分析AF中继选择(AF-RS)的性能。
(1)衰落信道下计算近似BER的通用方法
为了使AF-RS的分析更简单,首先介绍在衰落信道下计算近似BER的通用方法。3.2.4节中已经介绍了Wang和Giannakis提出的方法[383],对于不同的调制方式,BER可以通过下式计算:

式中,γ表示瞬时接收SNR;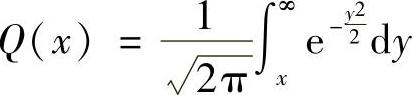 是Q函数;a、b是调制方式相关参数。表3.1中列出了不同调制方式下a、b的取值。经过计算,式(3.195)可以进一步写成
是Q函数;a、b是调制方式相关参数。表3.1中列出了不同调制方式下a、b的取值。经过计算,式(3.195)可以进一步写成
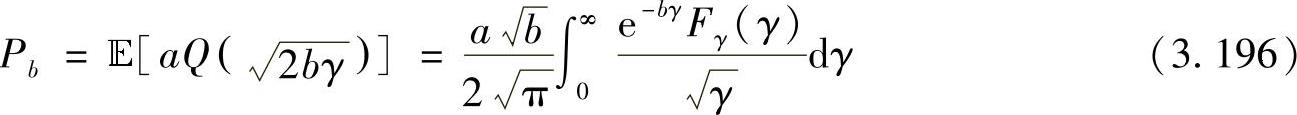
其中,Fγ(γ)是γ的CDF。由式(3.196)可以直接通过γ的CDF获得BER。γ的CDF还可以用来求得高SNR时的近似BER。尤其是利用γ的CDF的一阶展开可以在高SNR处获得近似SNR。如果γ的CDF可以写成如下表达式:
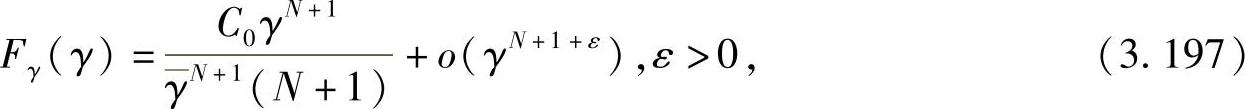
或者γ的PDF可以表示成
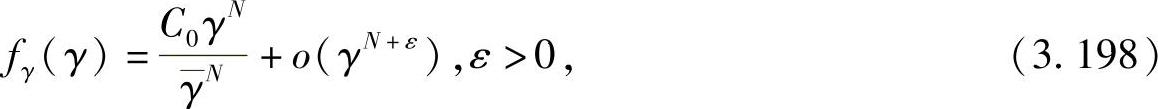
则高SNR下的BER可以表示成[383]
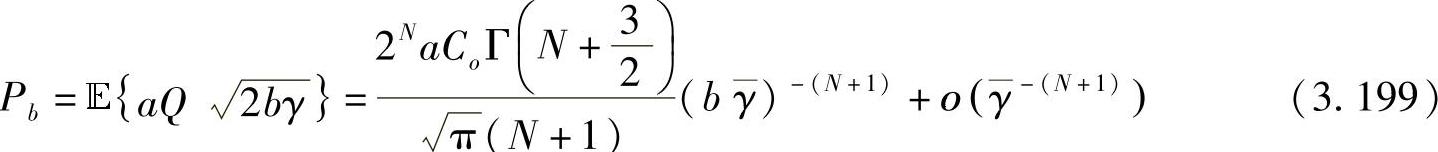
式中,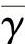 表示平均发射SNR。
表示平均发射SNR。
表3.1 不同调制方式下a、b取值

(2)多变量的顺序统计
为了分析AF-RS的性能,需要用到顺序统计的知识。本节中,为了便于理解随后的性能分析,首先简要介绍顺序统计的基本工具。读者如想全面了解顺序统计理论,可以参照文献[319]。
考虑n个独立同分布的随机变量X1,…Xn,其CDF均为F(x)。若将X1,…Xn按照升序排列,表示为
X(1)≤X(2)≤…≤X(N) (3.200)
我们将X(i)叫做第i个顺序统计(i=1,…,n)。则第i个顺序统计量Xi的CDF用F(i)(x)表示为
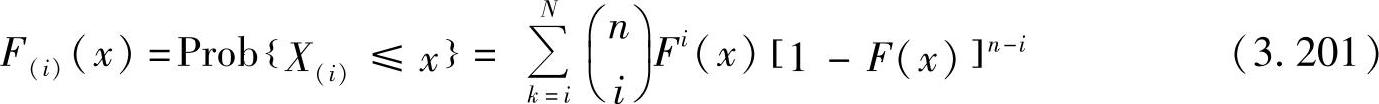
接下来考虑两个特殊情况,即X(1)和X(n)。分别将i=1和i=n代入上式中,得

通过对X(1)和X(n)的CDF求导可以获得它们的PDF:
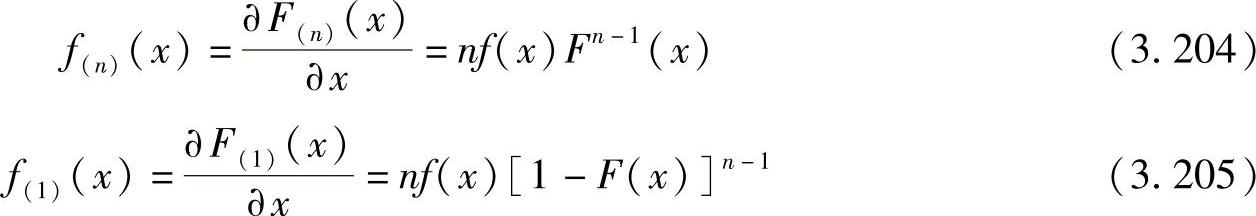
类似地,我们可以得到X(n1),…X(nk)(1≤n1≤n2<…<nk<n)对于x1≤x2≤…≤xk的联合PDF,有
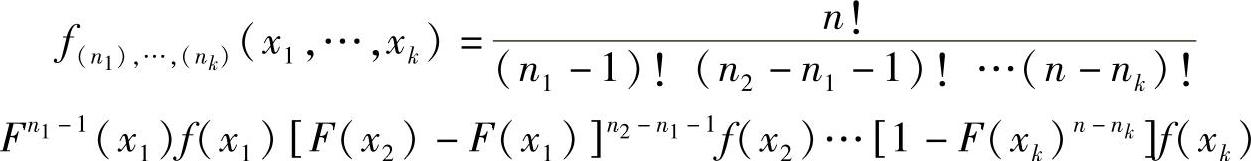
特别地,所有顺序统计的联合PDF可表示为
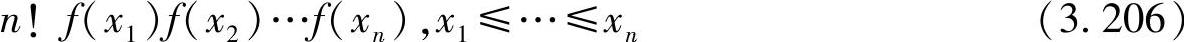
(3)两个随机变量的调和平均值
在3.4.2.1节中我们观察到中继链路i的目的节点的接收信噪比γiSRD的表达式,实际上可以把它看做是两个独立同伽玛分布的随机变量的修正调和平均值,因此这里我们先推导两个独立同伽玛分布的随机变量X和Y的调和平均值以及修正调和平均值。
两个随机变量X和Y的调和平均值定义为[274]:

则其修正调和平均值定义为[438-340]:

当C=0时式(3.208)则退化成调和平均[274,441]。我们用X~g(k,a)表示X服从伽玛分布,
其PDF可表示为

其CDF可表示为
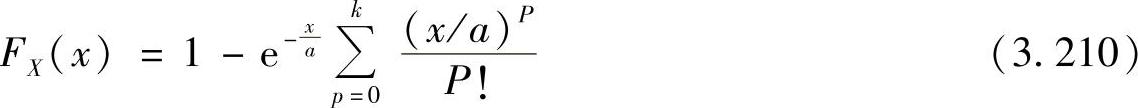
下面的定理给出了两个独立同伽玛分布的随机变量调和平均值的CDF。
定理3.4.1:令X、Y表示两个独立同伽玛分布的随机变量,X~g(k1,a1),Y~g(k2,a2)。则X、Y的修正调和平均值ZC=μMH(X,Y,C)的CDF可表示为
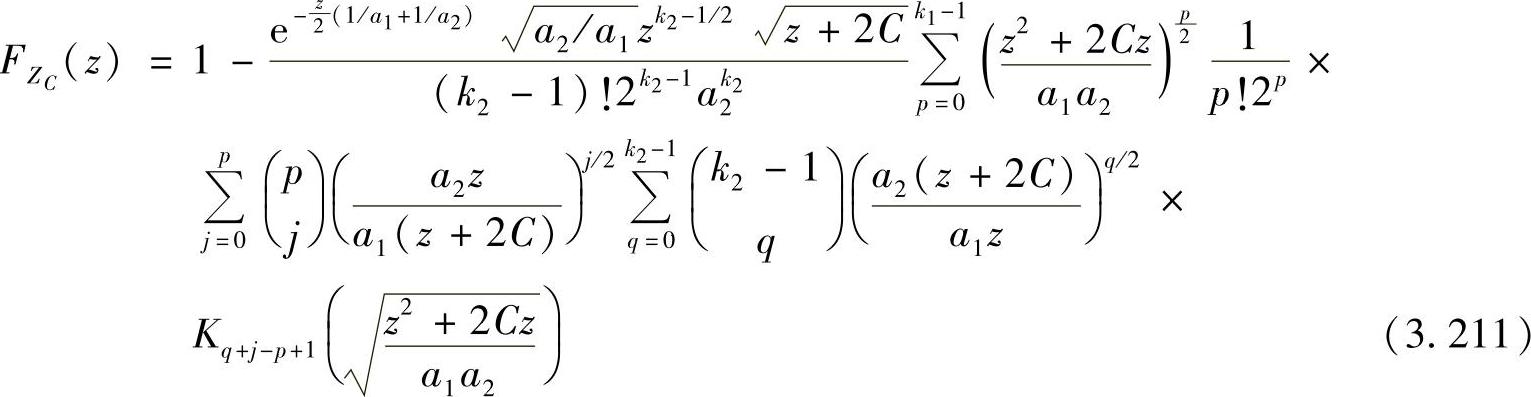
式中,Kν(·)为第二类ν阶修正贝塞尔函数。
将C=0代入上式,可以推导出两个独立同伽玛分布的随机变量的调和平均的分布,如下面推论所示[438]:
推论3.4.2:令X、Y表示两个独立同伽玛分布的随机变量,X~g(k1,a1),Y~g(k2,a2)。则X、Y的调和平均ZH=μH(X,Y)的CDF可表示为
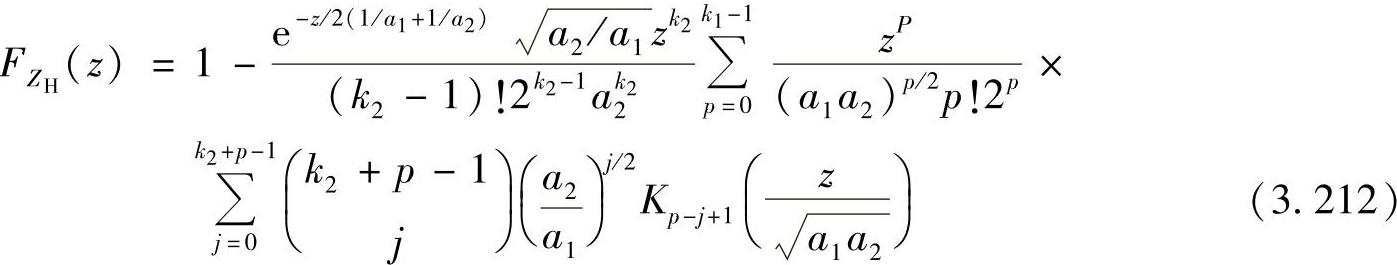 (https://www.xing528.com)
(https://www.xing528.com)
根据以上定理和推论,我们可以得到两个指数分布的随机变量的修正调和平均值的分布,如下面推论所示[438]。
推论3.4.3:两个独立同指数分布的随机变量Xe与Ye的PDF分别为fXe(xe)=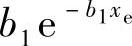 和
和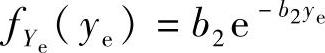 ,则Xe和Ye的修正调和平均ZMH,e=μMH(Xe,Ye,C)的CDF可以表示为
,则Xe和Ye的修正调和平均ZMH,e=μMH(Xe,Ye,C)的CDF可以表示为
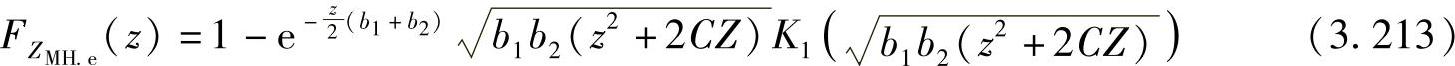
将k1=k2=1,b1=1/a1和b2=1/a2代入即可得到上述推论的证明。类似地,将C=0代入上式,可以推导两个独立同指数分布的随机变量的调和平均的分布。
推论3.4.4:两个独立同指数分布的随机变量Xe与Ye的PDF分别为fXe(xe)=b1e-b1xe与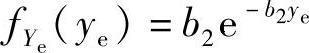 ,则Xe和Ye调和平均ZH,e=μH(Xe,Ye)的CDF可以表示为
,则Xe和Ye调和平均ZH,e=μH(Xe,Ye)的CDF可以表示为
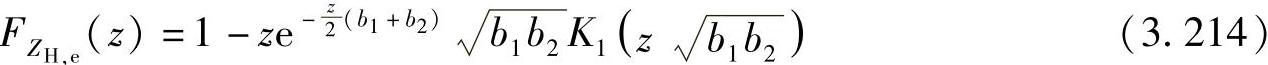
接下来的推论给出了两个独立同指数分布的随机变量Xe和Ye的调和平均和修正调和平均的PDF。
推论3.4.5:两个独立同指数分布的随机变量Xe与Ye的PDF分别为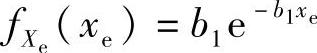 与
与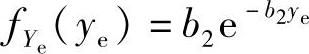 ,则Xe和Ye的修正调和平均
,则Xe和Ye的修正调和平均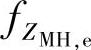 可以表示为[438]
可以表示为[438]
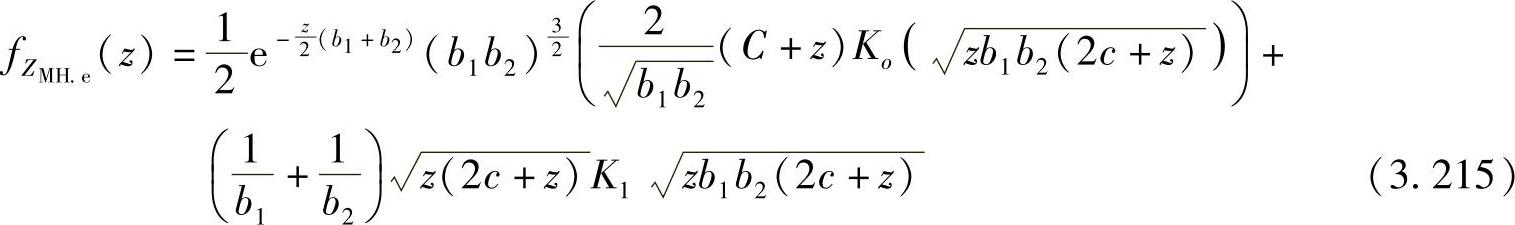
推论3.4.6:两个独立同指数分布的随机变量Xe与Ye的PDF分别为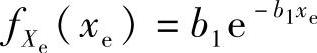 与
与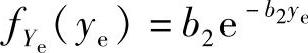 ,则Xe和Ye的调和平均值
,则Xe和Ye的调和平均值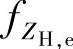 可以表示为[441]:
可以表示为[441]:
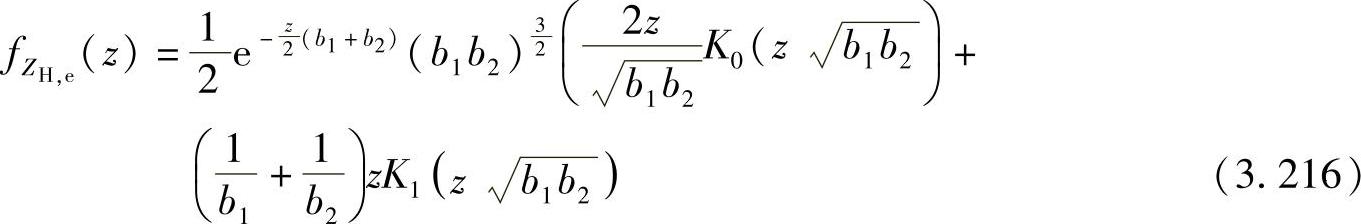
瑞利信道下AF中继选择的BER性能分析。利用上面介绍的基本分析工具,我们分析AF中继选择的系统性能。为了简化分析,调制方式采用BPSK。
令fSR,i(x)和fRD,i(x)分别表示γiSR和γiRD的PDF,它们均服从指数分布且其PDF为


我们首先计算中继链路i的目的节点的接收信噪比:
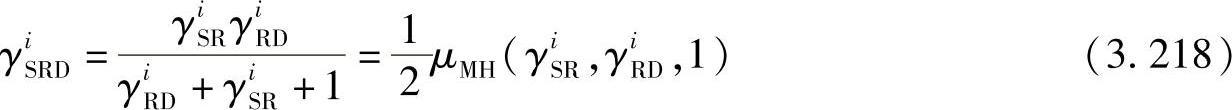
令fR(x)和FR(x)表示γiSRD的PDF和CDF,则其CDF可以通过将x=z/2,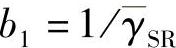 和b2=
和b2=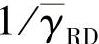 代入推论3.4.3得到:
代入推论3.4.3得到:
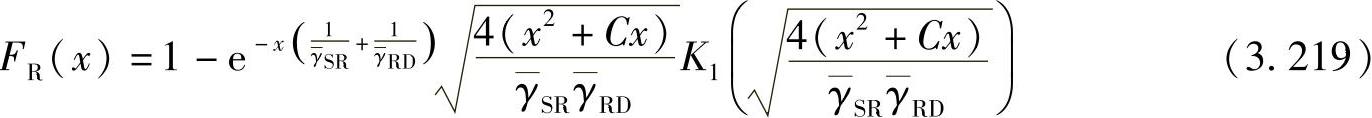
类似地,其PDF可以通过推论3.4.5获得:
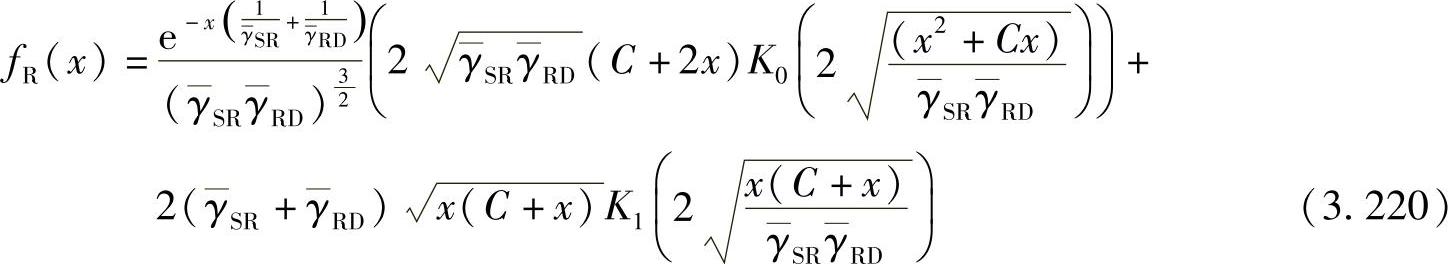
在AF中继选择策略中,选择具有最大链路SNR的单个中继S进行转发,而其他中继处于空闲状态,即

换句话说,如果我们将n条链路的SNR进行升序排列,即

则有:

按照3.4.2节中介绍的顺序统计理论来分析,γSSRD的CDF和PDF,F(S)(x)和f(S)(x),可以表示为
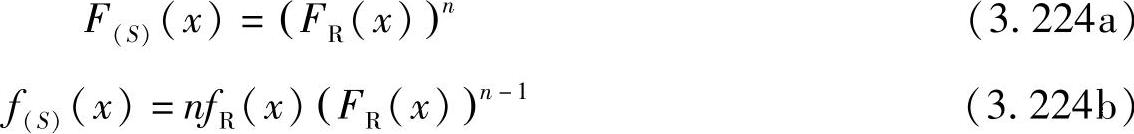
因为FR(x)和fR(x)的表达已经非常复杂,使用γSSRD的CDF和PDF来计算BER的复杂度太大。为了分析简化,我们只考虑高SNR时的近似处理:
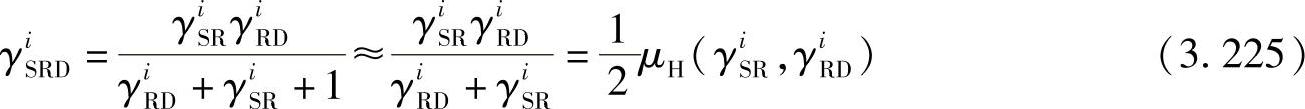
在高SNR时,γiSRD可以通过γiSR和γiRD的调和平均值来近似。类似地,使用推论3.4.4和3.4.6,γiSRD的CDF和PDF可以表示为
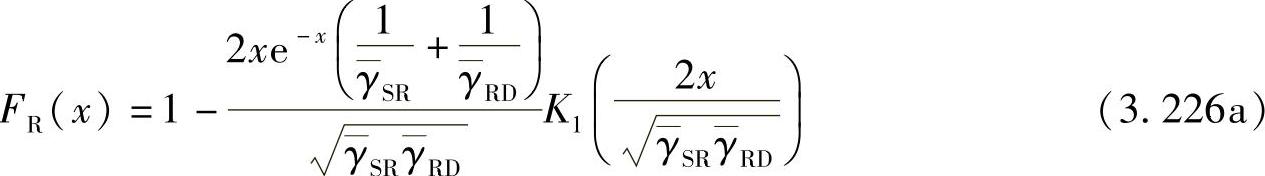
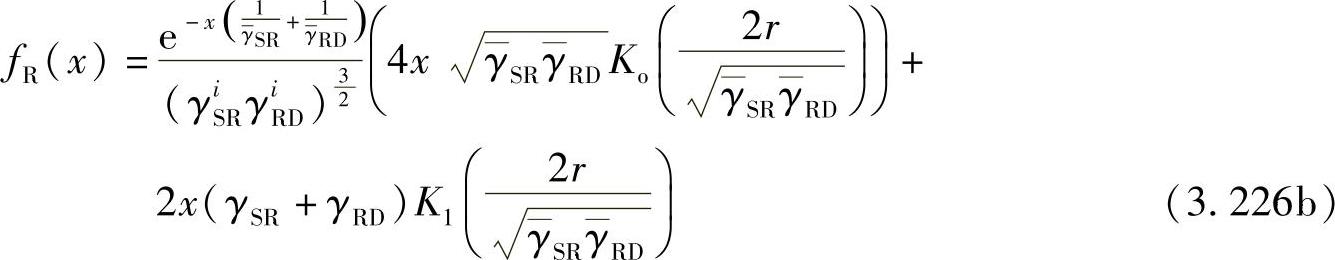
式(3.226a)和式(3.226b)包含修正贝塞尔函数,仍然很复杂,我们需要做进一步的近似。修正贝塞尔函数有如下性质:当x→0时K0(x)→0,K1(x)→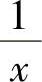 。利用此近似,式(3.226a)和式(3.226b)可以进一步化简为
。利用此近似,式(3.226a)和式(3.226b)可以进一步化简为
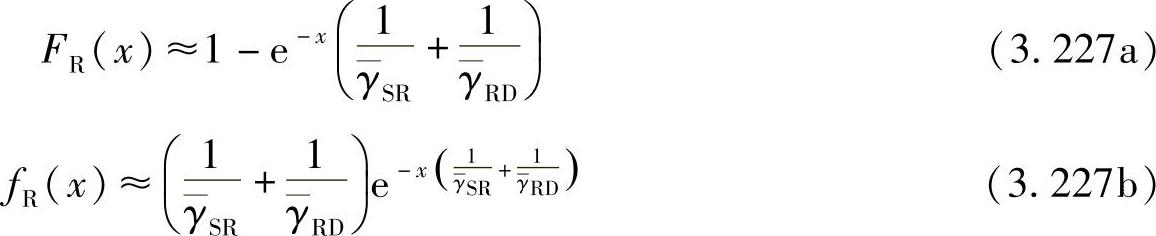
将γiSRD的CDF和PDF代入式(3.224a)和式(3.224b),则选择中继S后的目的节点的接收SNR可以近似为
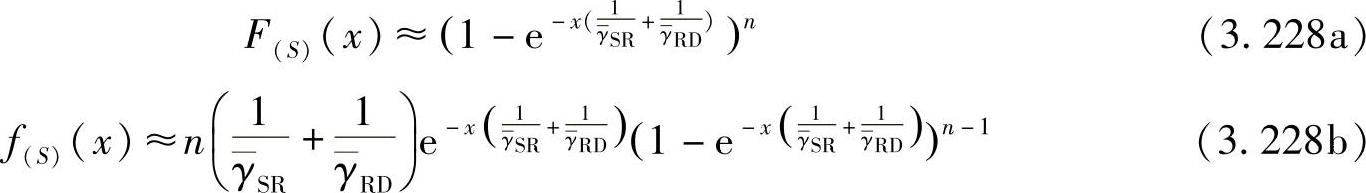
将式(3.228a)代入式(3.196),并且设置BPSK调制下a=1,b=1,则AF-RS的平均信噪比:
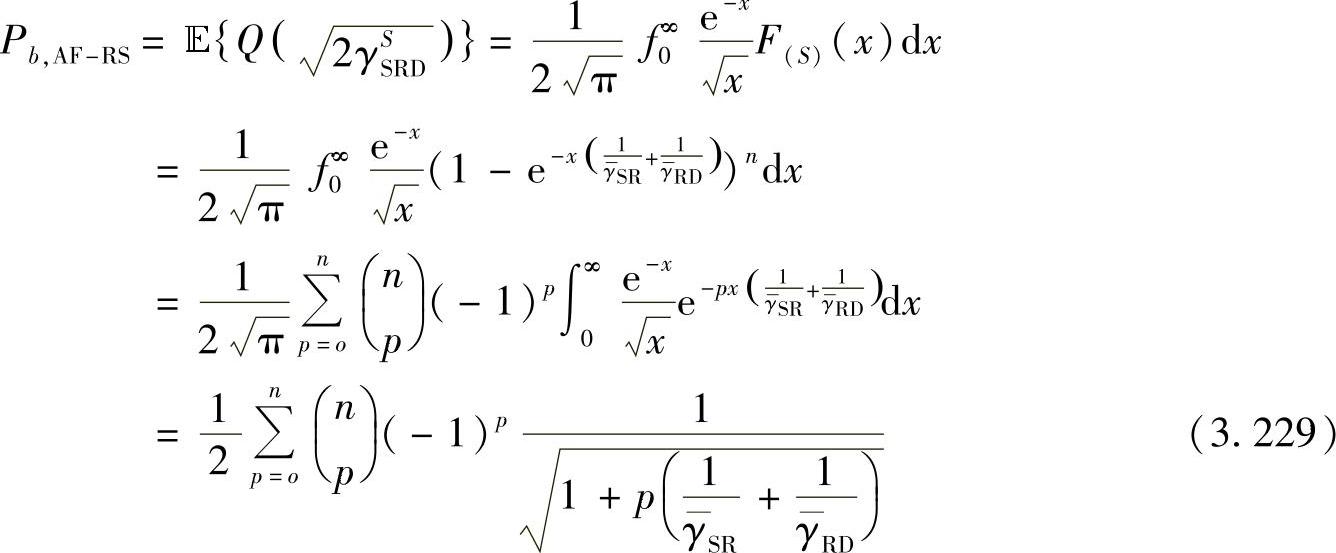
式中,Fγ(γ)是γ的CDF。在高SNR下,F(S)(x)的一阶展开为
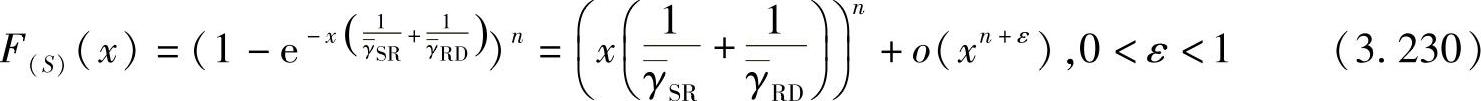
最后,在高SNR时AF-RS的BER可以近似为

我们从上式可以看出,AF中继选择策略也可以获得满分集度n。
3.4.2.3 仿真结果
本节我们给出了AF中继选择的仿真结果并与理论分析进行了对比。我们考虑无信道编码、BPSK调制方式的系统。图3.28~图3.30分别比较了具有不同中继数目时不同信噪比假设条件下的仿真与理论BER性能,其中x轴表示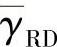 。从图中可以看出系统分集度随中继数量的增多而增加,而且随着SNR的增加,理论结果与仿真结果越来越接近。
。从图中可以看出系统分集度随中继数量的增多而增加,而且随着SNR的增加,理论结果与仿真结果越来越接近。
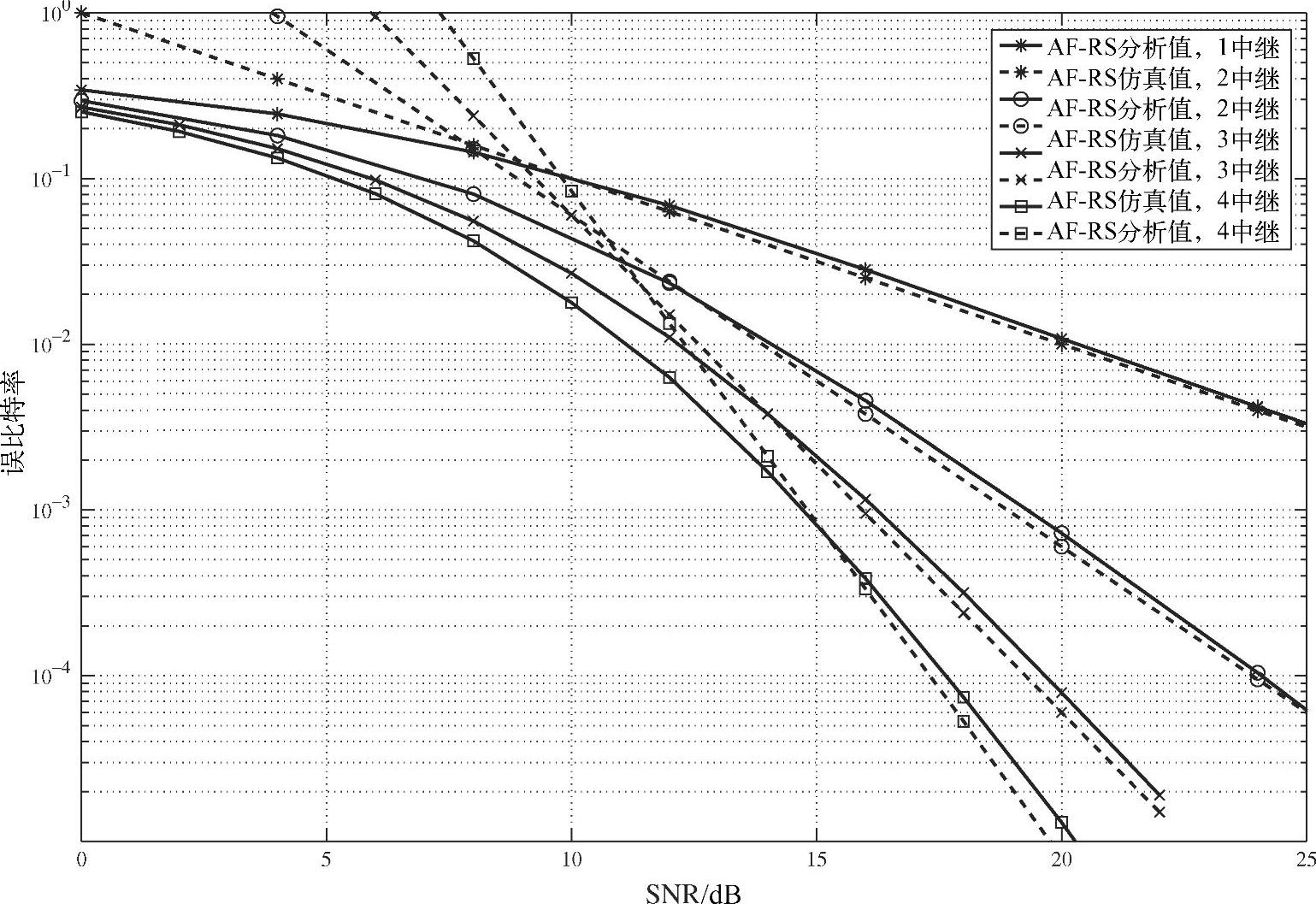
图3.28 具有不同中继数的AF-RS系统BER性能,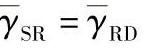
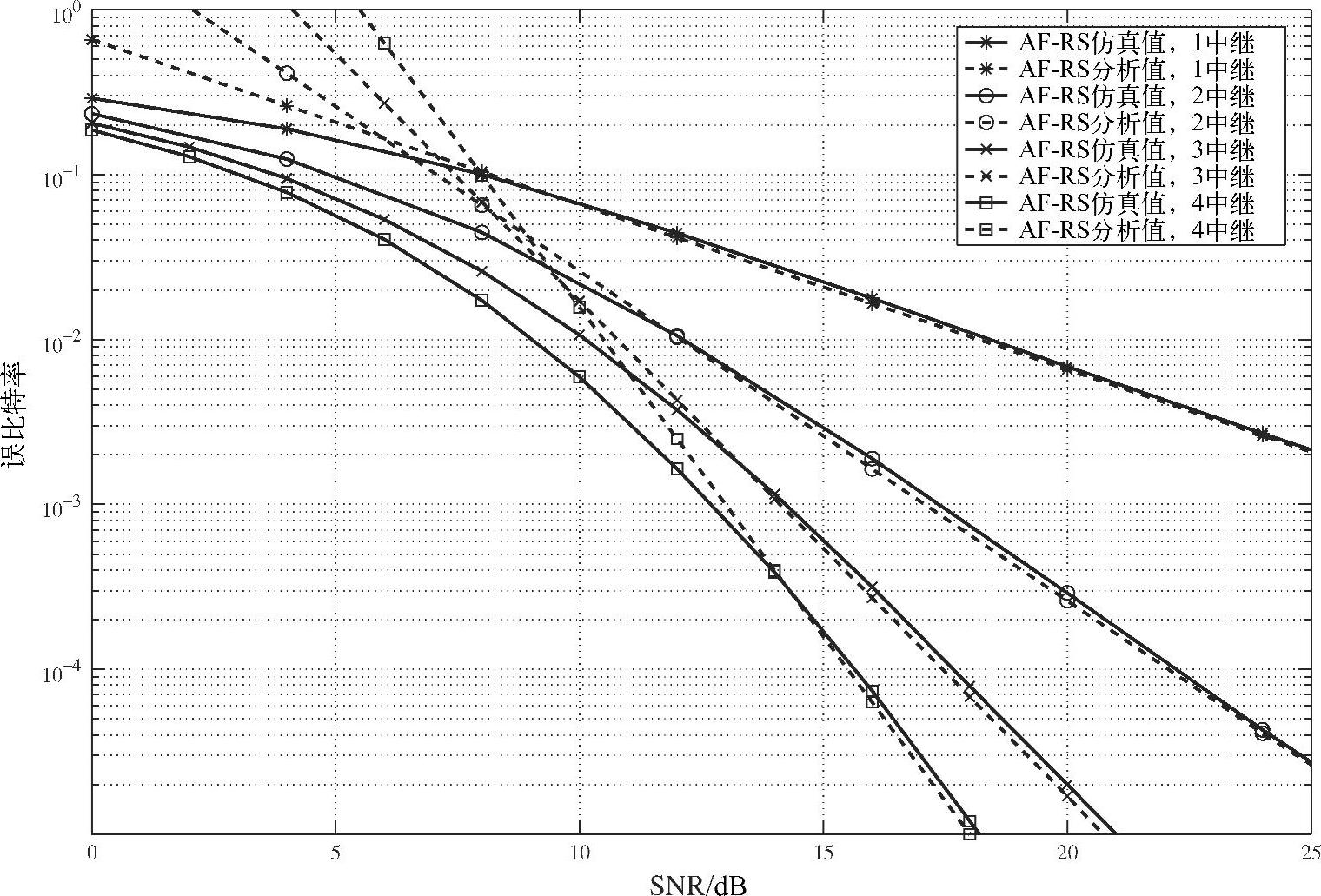
图3.29 具有不同中继数的AF-RS系统BER性能,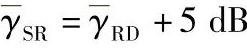
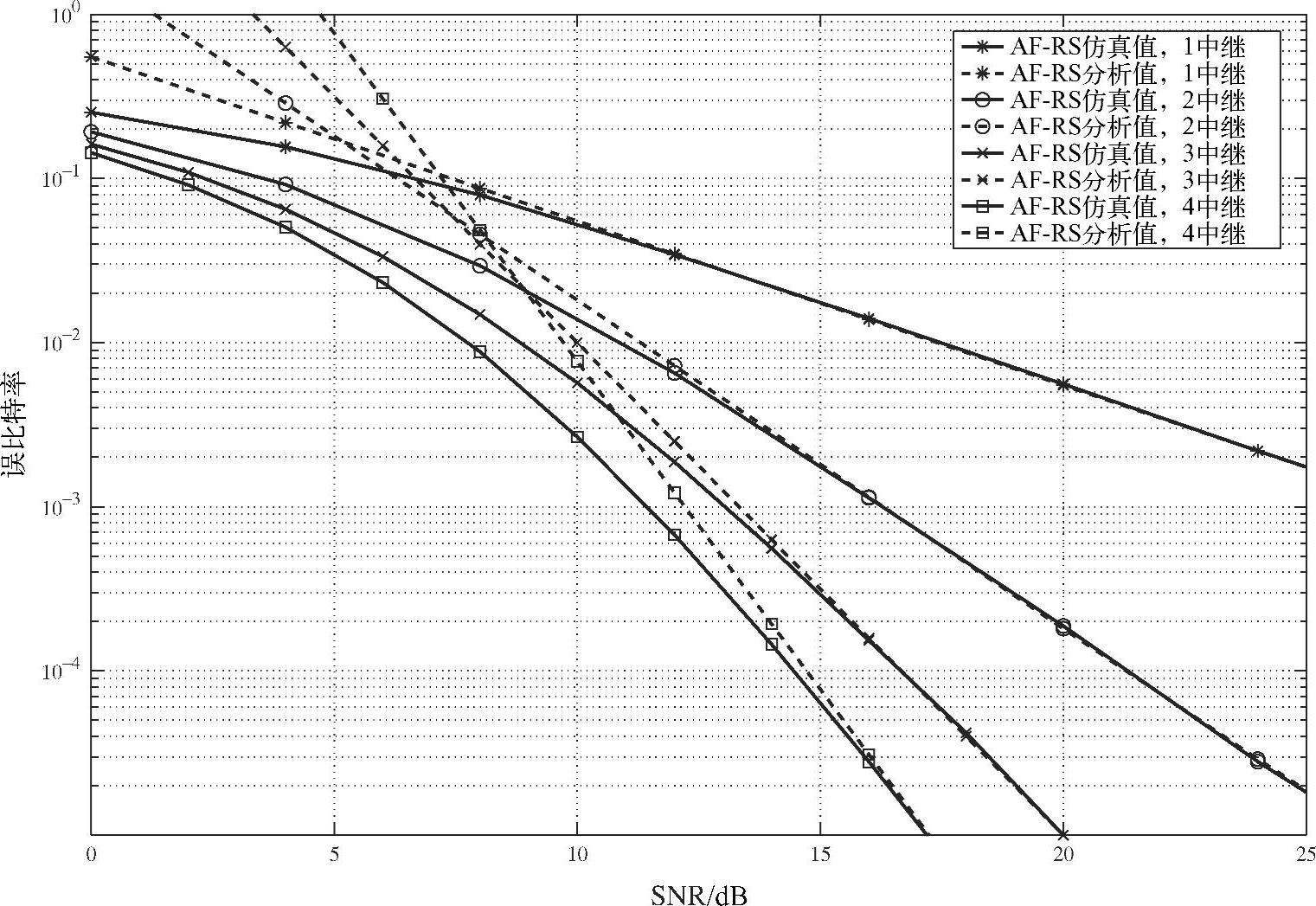
图3.30 具有不同中继数的AF-RS系统BER性能,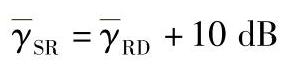
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




