众所周知,在MIMO系统中,当发送端不知道信道状态信息时,采用空时编码可以获得满空间分集和理想的编码增益;当发送端能够获得全部信道状态信息时,就可以进一步提高系统性能。一个特殊的例子是,发送端有目的地控制每根发送天线上的发送信息的相位和相对幅度,可在接收机的方向上形成场强较强的波束。发送端波束赋形已被证明是最优的传输方案。
同样,在无线协同网络中,分布式空时编码可以获得满分集度,这在3.3.1节中已经探讨过了。与MIMO系统一样,如果能有效利用中继节点处的信道状态信息,也能够有效地提高分布式系统的传输性能。线性的分布式处理技术,例如文献[124,420-429]中提出的分布式波束赋形和文献[430-434]提出的分布式MMSE,相对于分布式空时编码具有明显的性能优势。传统的MIMO系统中的波束赋形和无线中继系统中的波束赋形的差别如下:
●集中式天线和分布式天线:对于传统的波束赋形来说,进行波束赋形的不同天线属于同一个发送端,这样可以联合设计最优的波束赋形矢量;而对于分布式波束赋形系统来说,天线与中继位于空间的不同位置,每个中继需要根据自己的信道状态信息和目的节点反馈的部分信道状态信息进行最优波束赋型矢量的设计。也就是说,分布式无线网络中,波束赋形的设计需分布式进行。
●完全和部分信道信息:在MIMO系统中,每根天线都拥有完全的发送数据信息,而对于分布式网络,中继处的接收信号带有噪声,也就是说每个中继只能得到源信息的估计值。因此,在分布式系统中,在分布式波束赋形矢量设计时,必须要考虑噪声和估计误差的影响。
这些区别使得分布式系统中的波束赋形设计更加复杂。在本节中,我们讨论AF转发协议下的分布式波束赋形的设计。在波束赋形矢量的设计中,要满足以下两种功率限制条件:①全局功率和限制,所有中继的总发射功率不能超过给定的功率值;②单个中继功率限制,每个中继具有自己的功率限制值。
3.3.4.1 系统模型
再次考虑包含一个源节点、多个中继节点和一个目的节点的通用两跳中继系统,且源节点和中继节点之间不存在直接链路,则两跳分布式波束赋形系统的框图如图3.22所示。
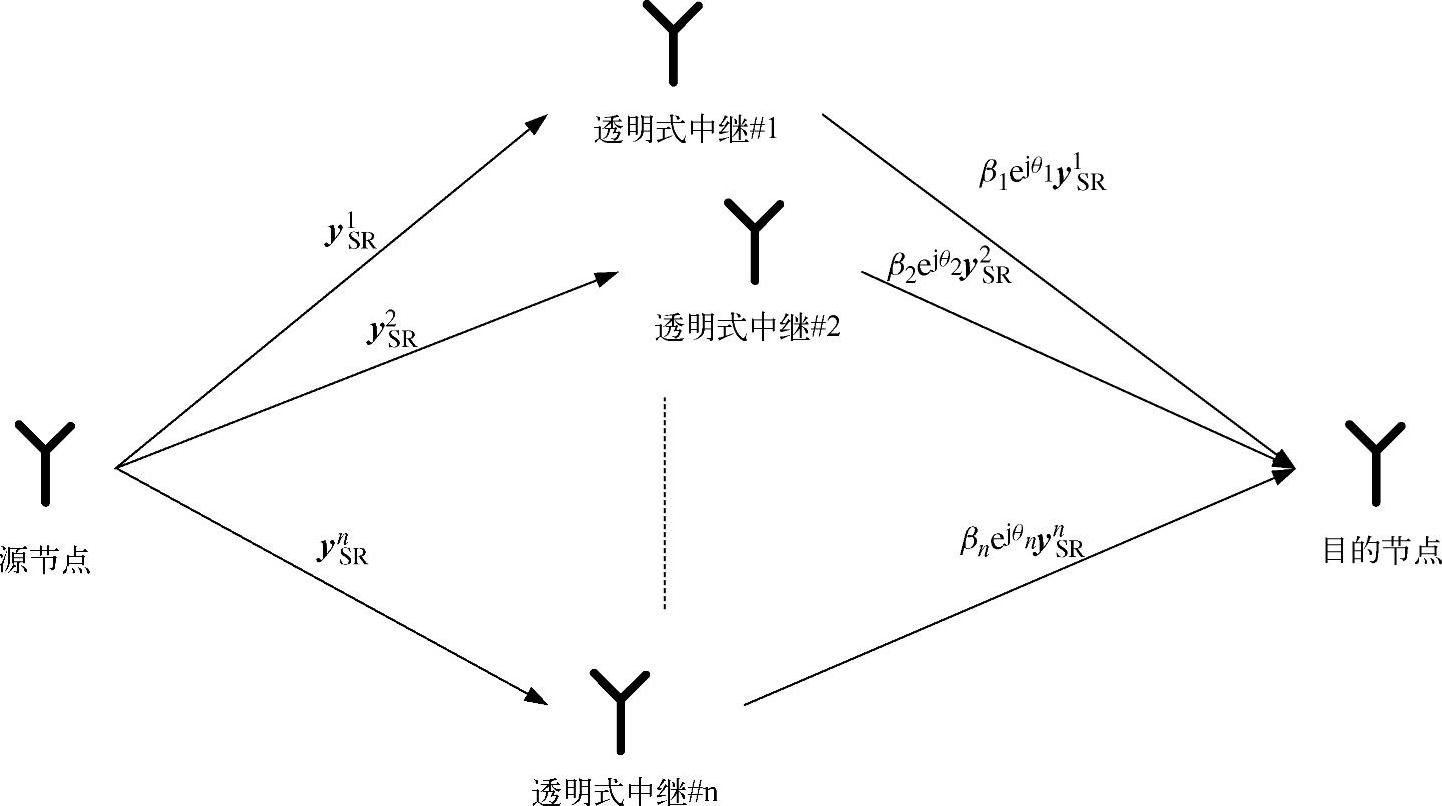
图3.22 通用两跳分布式波束赋形系统框图
源节点广播信息x至所有中继节点,第i个中继的接收信号为

其中,piSR=ps(GiSR)2表示第i个中继的接收信号功率;ps是源节点的发送功率;GiSR是源节点和第i个中继的信道增益;hiSR是源节点和第i个中继链路的信道系数;niSR是噪声矢量,它是服从零均值、双边功率谱密度为N0/2的复高斯随机变量。
第i个中继接收到源节点发送的信号后,对其进行处理,并将处理后的信号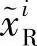 转发至目的节点:
转发至目的节点:
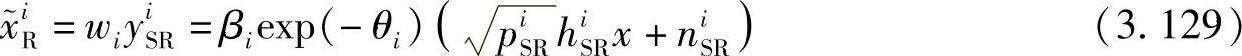
其中,βi是功率分配因子,需满足中继i处传输功率限制:

其中,pR,i表示中继i的分配功率值。
目的节点处的接收信号为
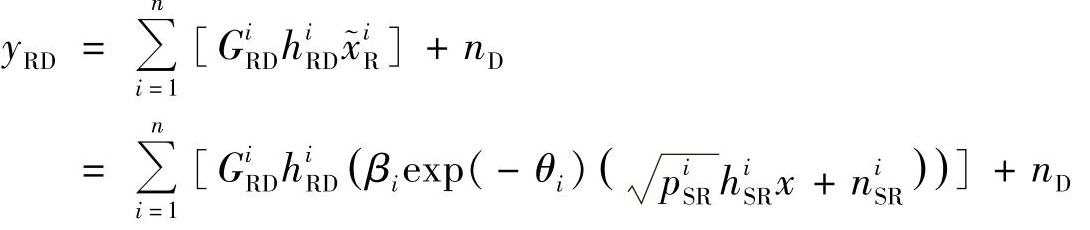
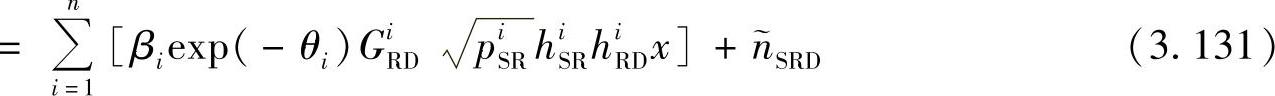
其中,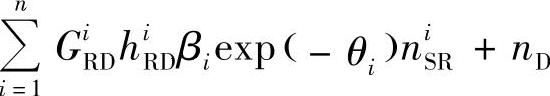 是目的节点处的等效噪声,其方差为
是目的节点处的等效噪声,其方差为
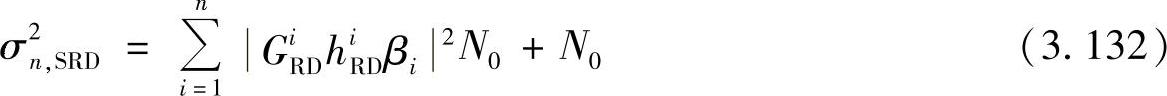
3.3.4.2 全局功率和限制下的设计
在本节中,我们将在全局功率和限制条件下,设计最优的波束赋形系数wi=βiexp(-θi),i=1,2,…,n。全局功率和限制条件为

在此,通过最大化目的节点处的SNR值来获得最优的波束赋形系数。由式(3.131)可以得到目的节点处的接收SNR:
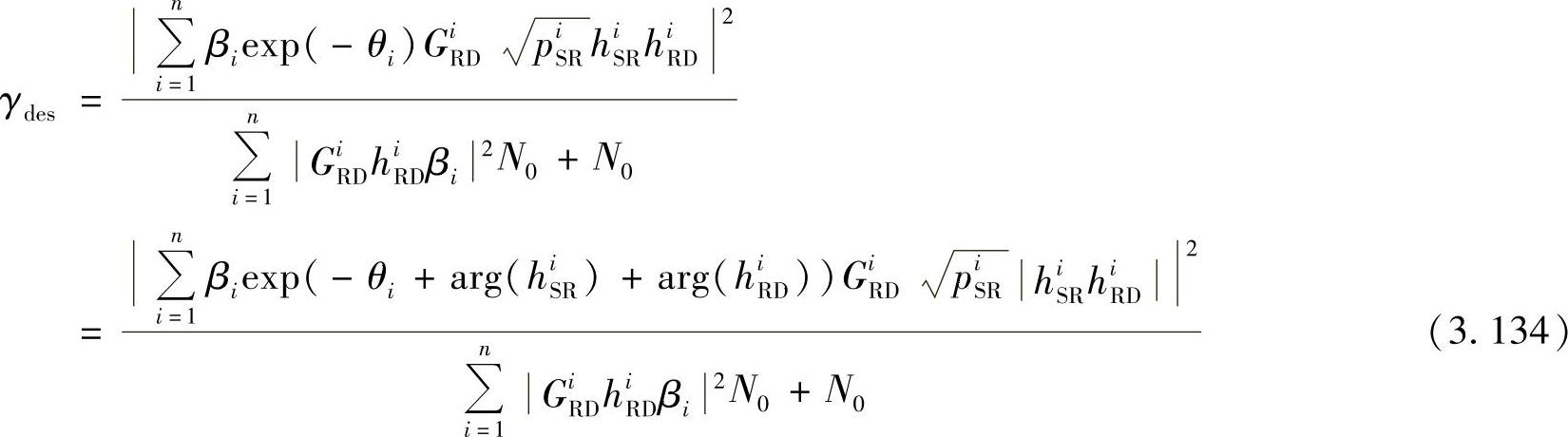
从式(3.134)可知,当下式所示的条件满足时可得到最大的SNR:

即波束赋型系数的最优相位θi为

中继节点采用匹配滤波器来抵消信道的相位。
将式(3.136)和式(3.130)代入式(3.134)中:
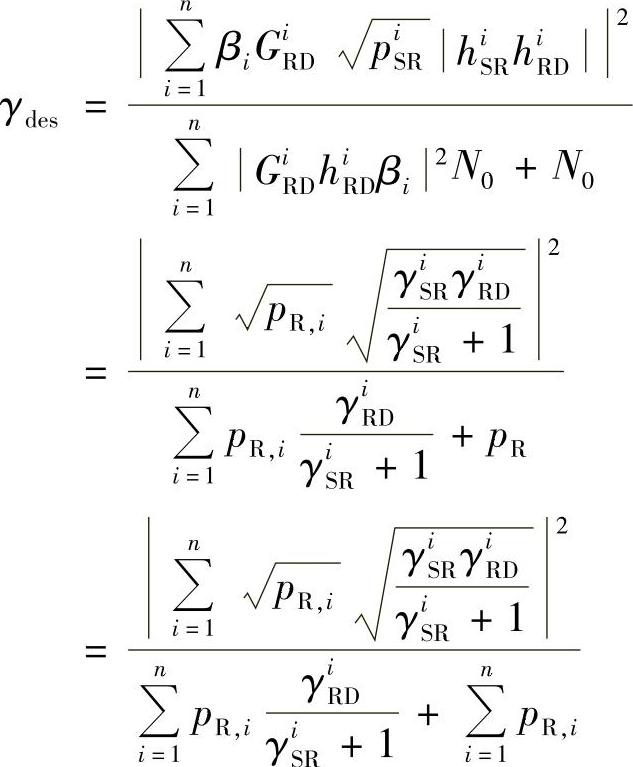
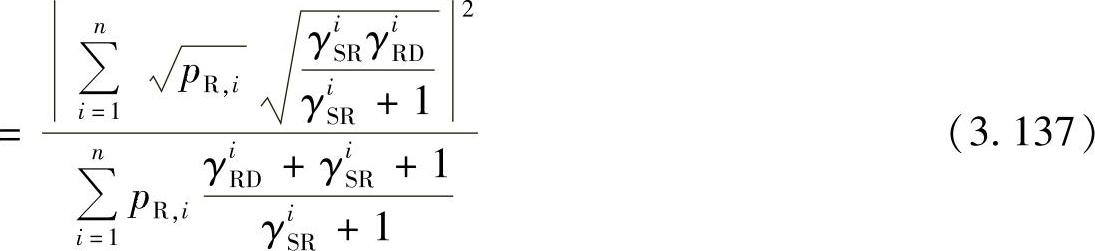
其中,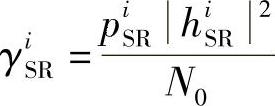 ,
,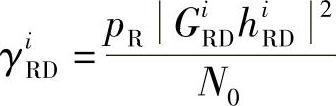 。
。
令
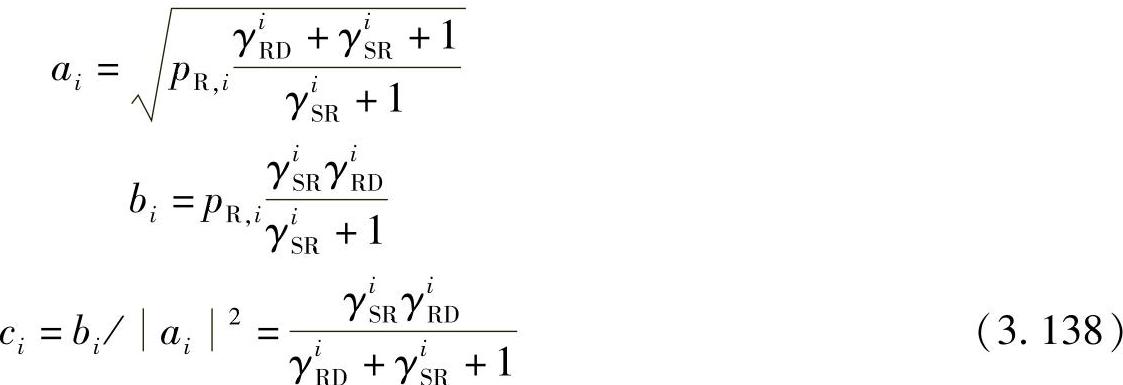
则式(3.137)可以进一步等效为
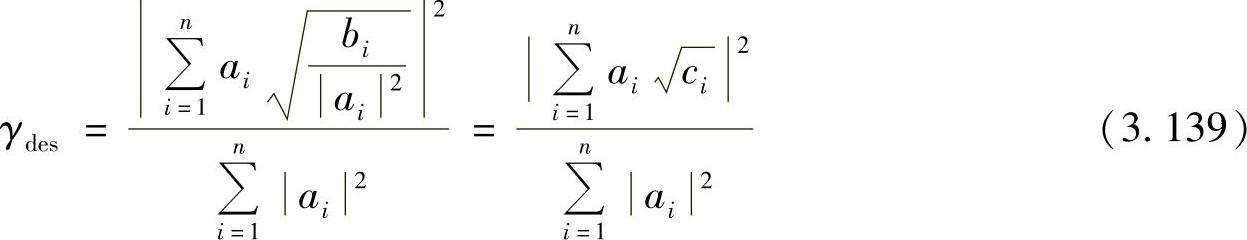
通过使用如下所示的Cauchy-Schwarz不等式:
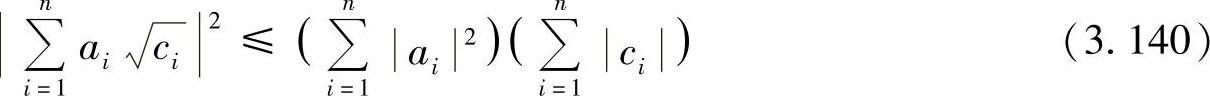
并将式(3.140)代入式(3.139):

满足信噪比SNR最大化的充要条件为

式中,C0是常数。从式(3.142)可以得到最优功率分配参数[124]:

将式(3.143)代入式(3.133),可以得到
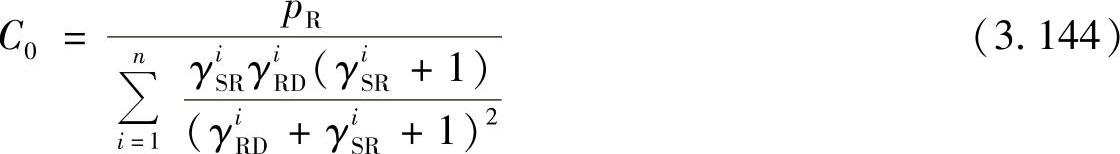
将式(3.143)和式(3.144)代入式(3.130),可以得到中继i的最优波束赋型矢量:
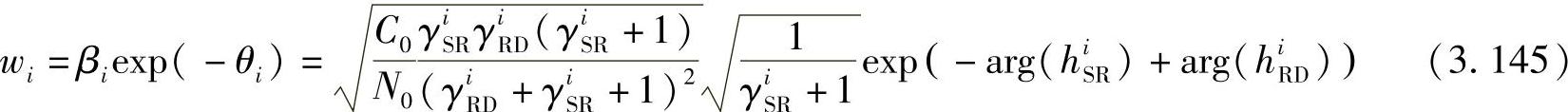
从式(3.145)可见,若想使用分布式波束赋型技术,每个中继节点可以通过自身的上、下行信道信息γiSR、γiRD和常数C0决定其传输功率和相位,其中C0对每个中继节点均相同,因而可以通过广播信道周期从目的节点获得。
在全局功率控制约束下,分布式波束赋型的最大SNR为

从式(3.146)可以看出,分布式波束赋型方案下的接收SNR表达式与使用最大比合并(MRC)的AF系统接收SNR表达式非常相似,此处的MRC合并可理解为在正交信道上传输的多个中继接收信号进行MRC合并。所以,该方案的容量、BER和中断概率均与3.2节对于AF系统的分析类似。
3.3.4.3 单个中继功率限制下的设计
在3.3.4.2节中讨论的基于全局总功率限制的最优波束赋型设计中,通过调整每个中继站的发射功率以优化接收SNR,从而将所有中继站的总功率控制在一定范围内,但是这种设计方法对单个中继的发射功率没有限制。实际系统中每个中继都配有电源设备,所以对单个中继进行功率限制的方案更为实际。文献[427]分析了单个中继功率限制下的波束赋型设计,与全局总功率受限的情况相比,其功率分配算法有所不同。在单个中继功率限制的要求下,一些中继站为了达到最优SNR可能不会以最大功率发射。本节基于文献[423,427]的研究结果分析在单个中继功率受限条件下的波束赋型设计。
我们考虑与3.3.4节相同的系统模型,并采用与3.3.4节相同的计算方法可得到目的节点接收信号的SNR表达式:
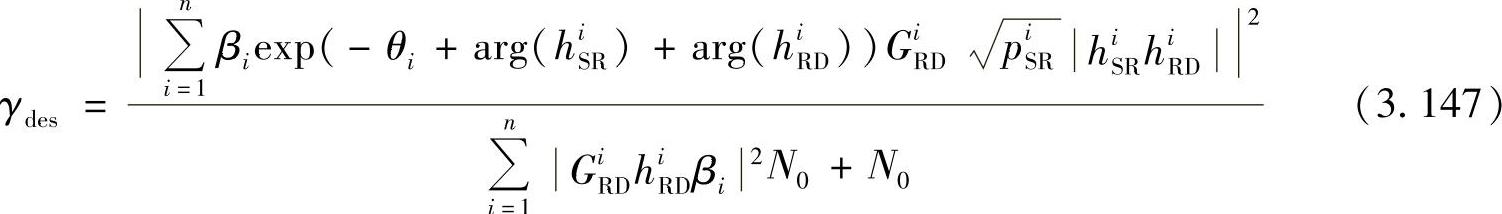 (https://www.xing528.com)
(https://www.xing528.com)
式中,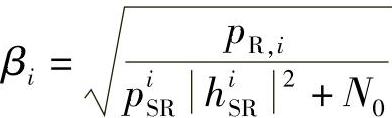 是中继节点i的放大因子,pR,i=piα2i,pi是中继节点i的传输功率限制,0≤αi≤1表示中继节点i的功率分配因子。
是中继节点i的放大因子,pR,i=piα2i,pi是中继节点i的传输功率限制,0≤αi≤1表示中继节点i的功率分配因子。
与3.3.4节的讨论相似,当满足-θi+arg(hiSR)+arg(hiRD)=0时,接收SNR最大。将此条件代入式(3.147),可以将目的节点的接收SNR重新表达如下:
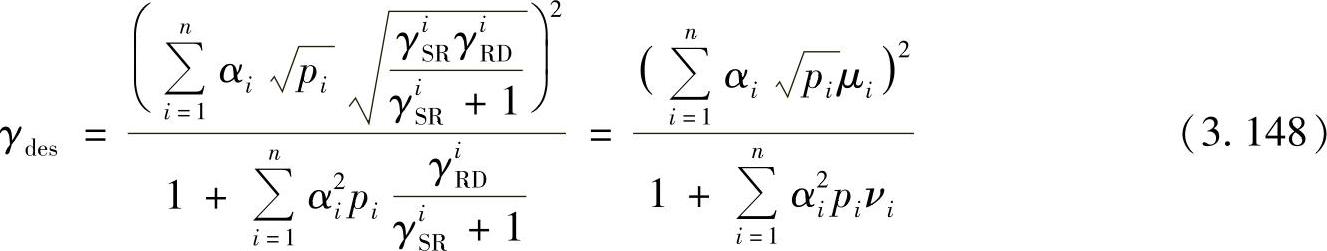
式中,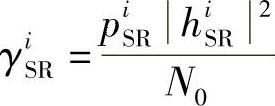 ,γ
,γ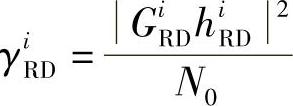 (注意这里γiRD的定义与式(3.137)有所不同),且
(注意这里γiRD的定义与式(3.137)有所不同),且

单个中继功率受限的波束赋型设计是通过寻找最优的功率分配因子0≤αi≤1,i=1,…,n,从而使式(3.148)中的目的节点接收SNR最大。将接收SNR表示为αi的函数(i=1,…,n),最优化问题为
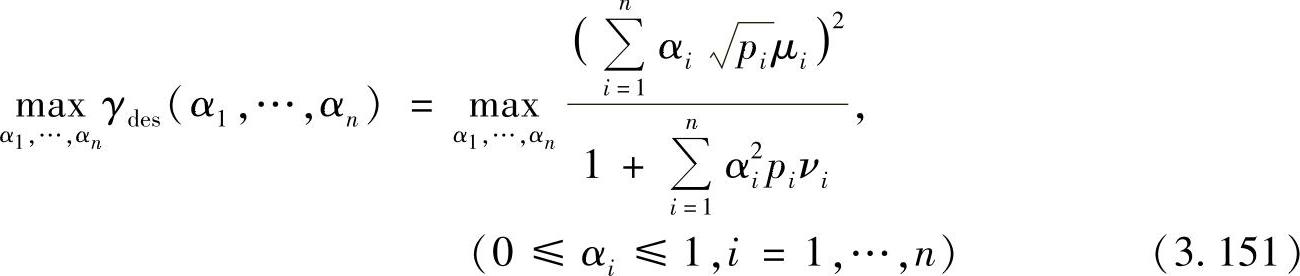
为了找到最优的功率分配因子0≤αi≤1,i=1,…,n,首先将式(3.151)对αi求导:
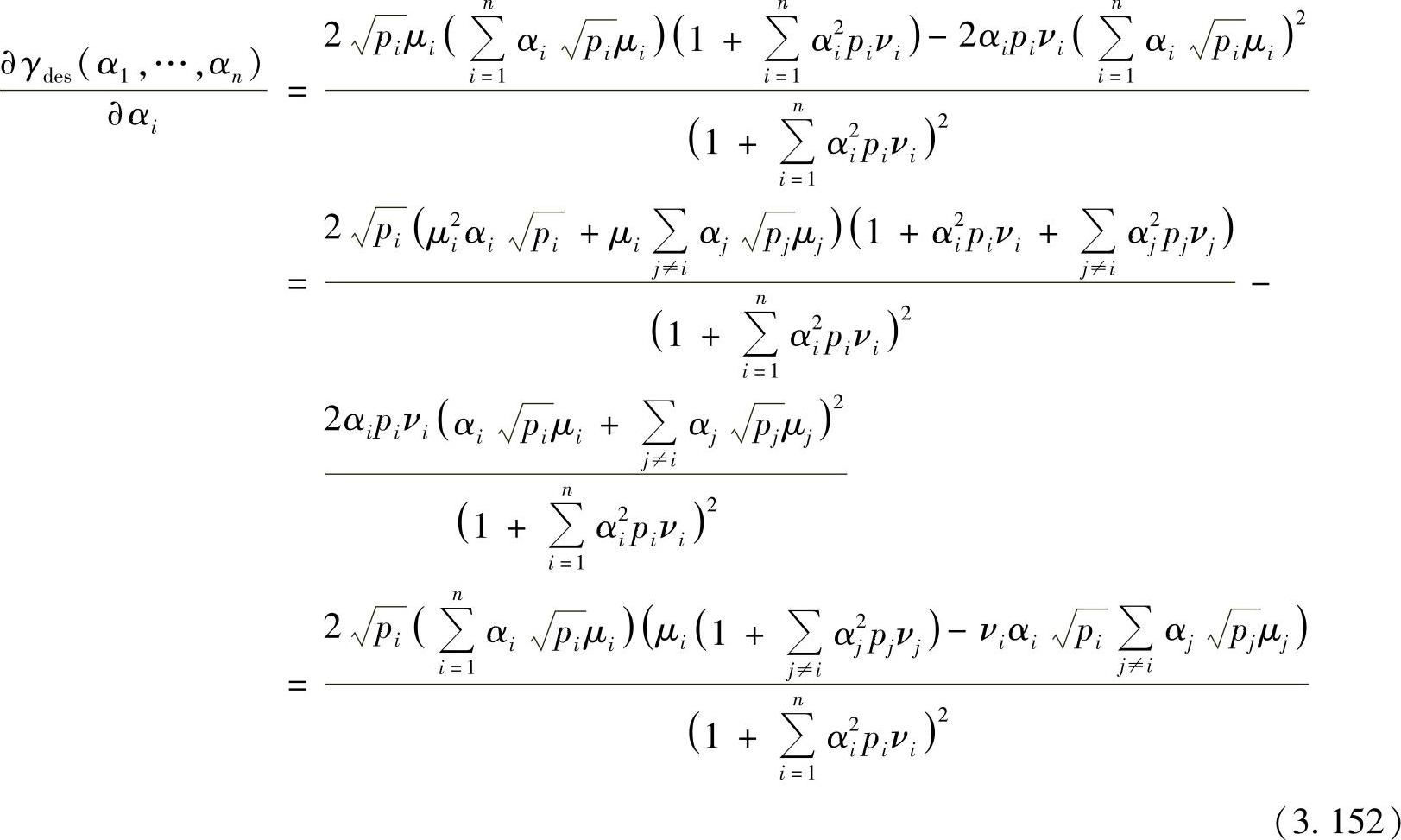
定义:

从上式可以看出:
如果αi<ϕi则 
如果αi>ϕi则 
如果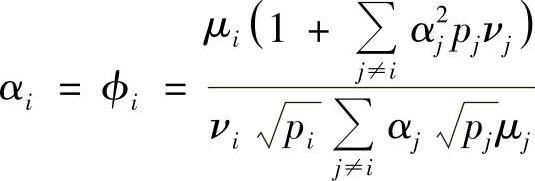 则
则
由此可见功率分配因子α1,…,αi相互关联,所以求解最优功率分配因子将非常复杂。我们首先在只有两个中继节点的简单模型下求解优化问题,可得

令αopti表示最优功率分配因子。进而得到以下定理[423]:
定理3.3.6:在一个包含两个中继节点的中继网络中,令γdes(α1,α2)表示单个中继功率受限条件下采用波束赋型时目的节点的接收SNR,则最优功率分配因子有如下性质[423]:
(i)当满足αo1pt=1或者α2opt=1时,γdes(α1,α2)可以取其最大值。
(ii)当α1opt=1时,γdes(α1,α2)在α2opt=min{1,ϕ2|α1=1}时取最大值,其中ϕ2|α1=1是将α1=1代入ϕ2所得的值,即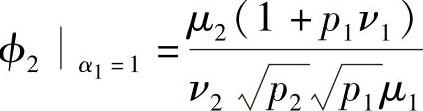 。
。
(iii)当α2opt=1时,γdes(α1,α2)在α1opt=min{1,ϕ1|α2=1}时取最大值,此时,ϕ1|α2=1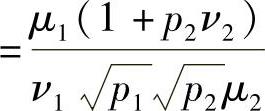 。
。
(iv)因此,当γdes(1,min{1,ϕ2})>γdes(1,min{1,ϕ1},1)时,最优的功控策略为α1opt=1,α2opt=min{1,ϕ2};否则最优功控策略变为α1opt=min{1,ϕ1},α2opt=1。
在文献[423]中给出了上述定理的完整证明,这里简要总结如下:
首先证明性质(i),我们定义
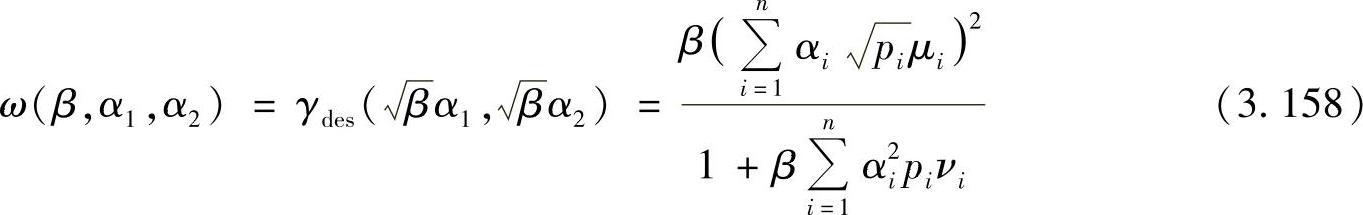
进一步有
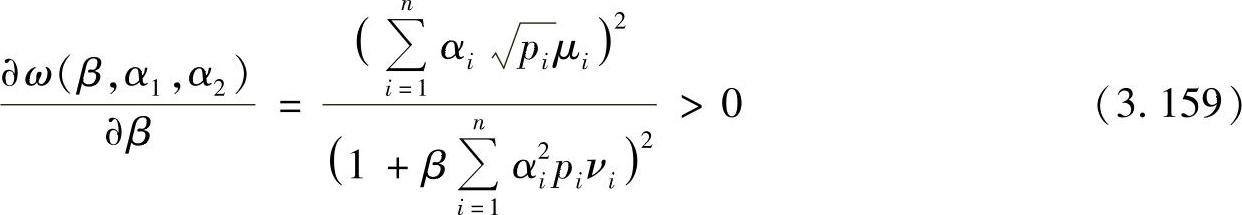
因此函数ω(β,α1,α2)=γdes(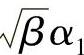 ,
,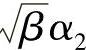 )是β的递增函数。假设0≤α1opt≤1,0≤α2opt≤1。不失一般性,假设α1opt≥α2opt。令β0=1/(α1opt)2,有β0>1,则
)是β的递增函数。假设0≤α1opt≤1,0≤α2opt≤1。不失一般性,假设α1opt≥α2opt。令β0=1/(α1opt)2,有β0>1,则
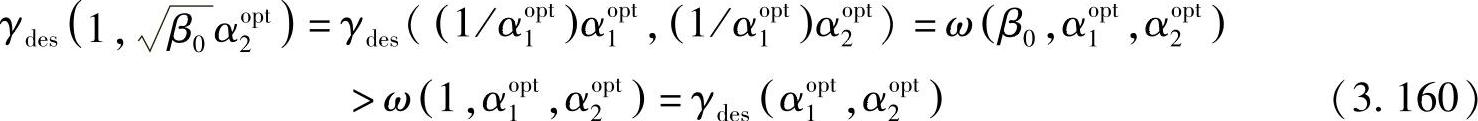
然而这与α1opt和α2opt是最优策略相矛盾,所以条件(i)得证。
性质(ii)和(iii)对称,所以我们只需证明其中一个,这里我们证明性质(ii)。如式(3.154a)和式(3.154b)所示,当α2<ϕ2时,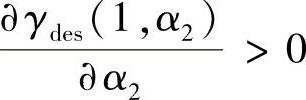 ;当α2>ϕ2时,
;当α2>ϕ2时,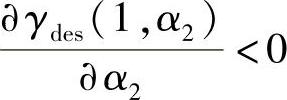 ,所以,γdes(1,α2)在ϕ2时取最大值。但是,功率分配因子的取值范围在[0,1]内,即0≤α1≤1,0≤α2≤1。如果ϕ2≤1,α2的最优取值为α2opt=ϕ2;如果ϕ2>1,α2≤1<ϕ2。由式(3.154a)可以得到
,所以,γdes(1,α2)在ϕ2时取最大值。但是,功率分配因子的取值范围在[0,1]内,即0≤α1≤1,0≤α2≤1。如果ϕ2≤1,α2的最优取值为α2opt=ϕ2;如果ϕ2>1,α2≤1<ϕ2。由式(3.154a)可以得到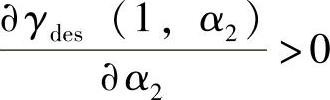 ,则在0≤α2≤1范围内γdes(1,α2)是α2的单调增函数,并可在α2=1时取到最大值。至此性质(ii)得证。类似地,可以证明性质(iii)。基于性质(ii)和(iii)可以直接得到性质(iv)的结论。
,则在0≤α2≤1范围内γdes(1,α2)是α2的单调增函数,并可在α2=1时取到最大值。至此性质(ii)得证。类似地,可以证明性质(iii)。基于性质(ii)和(iii)可以直接得到性质(iv)的结论。
从上述针对两个中继站的定理可以看出,在单个中继功率受限条件下为了获得最大的目的节点接收SNR,至少一个中继需以最大功率发射,而另一中继无需以最大功率发射,其具体功率分配值不仅与自身信道环境相关,也与其他中继的信道环境相关。
接下来我们讨论具有任意数目的中继节点的系统。对于超过两个中继的拓扑,最优功率分配因子的系统表达式非常复杂,这里我们直接给出最终解而省略掉所有证明过程。证明细节可以参照文献[427]。
定义
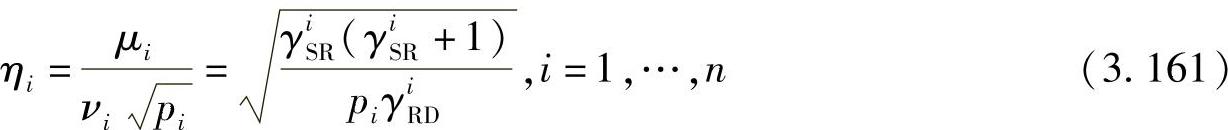
和
ηn+1=0 (3.162)
我们将ηi按降序排列:

式中,ηκn+1=ηn+1=0。
定义

对于选择最优功率分配因子的最优化问题可以通过下面的定理进行总结[427]:
定理3.3.7:定义αi=(αi(1),αi(2),…,αi(n)),如果
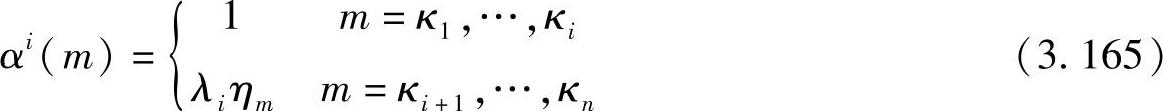
则单个中继功率受限下的最优功率分配因子为αopt=αi0,其中i0取i的最小值,满足λiηKi+1<1。
从上面的定理我们可以得到与只包含两个中继的系统相类似的结论:在单个中继功率受限条件下,为了得到最大的目的节点接收SNR,并不是所有中继都要以最大功率发射。只有η最大的i0个中继使用最大发射功率,而其他n-i0个中继只需要使用部分发射功率即可。并非所有中继都使用其最大发射功率的原因在于:对于每个中继,其发射功率都有对目的节点SNR起到两个相互冲突的作用。一方面,提高发射功率可以使目的节点的信号功率提高;另一方面,提高中继发射功率同时会相应提高目的节点的噪声功率,因为噪声功率在中继处被放大。
每个中继的最优功率也依赖于其他中继的信道环境,当目的节点已知所有中继的信道衰落及最大传输功率时,功率控制可以在接收端集中处理。从式(3.161)、式(3.164)和式(3.165)可知,每个中继为了计算最优功率分配参数,除了要知道自身最大发射功率和信道环境外还要已知一个通用参数λi0。这样,目的节点将广播这个通用参数λi0以及使用最大发射功率的中继节点序号。当中继节点从目的节点接收到其序号指示,将使用自身最大功率发射接收到的信号;如果中继节点没有接收到序号指示,它将使用λi0、自身信道信息和功率信息根据式(3.161)、式(3.164)和式(3.165)计算其发射功率。图3.23是单个中继功率受限的分布式波束赋型系统的传输框图。
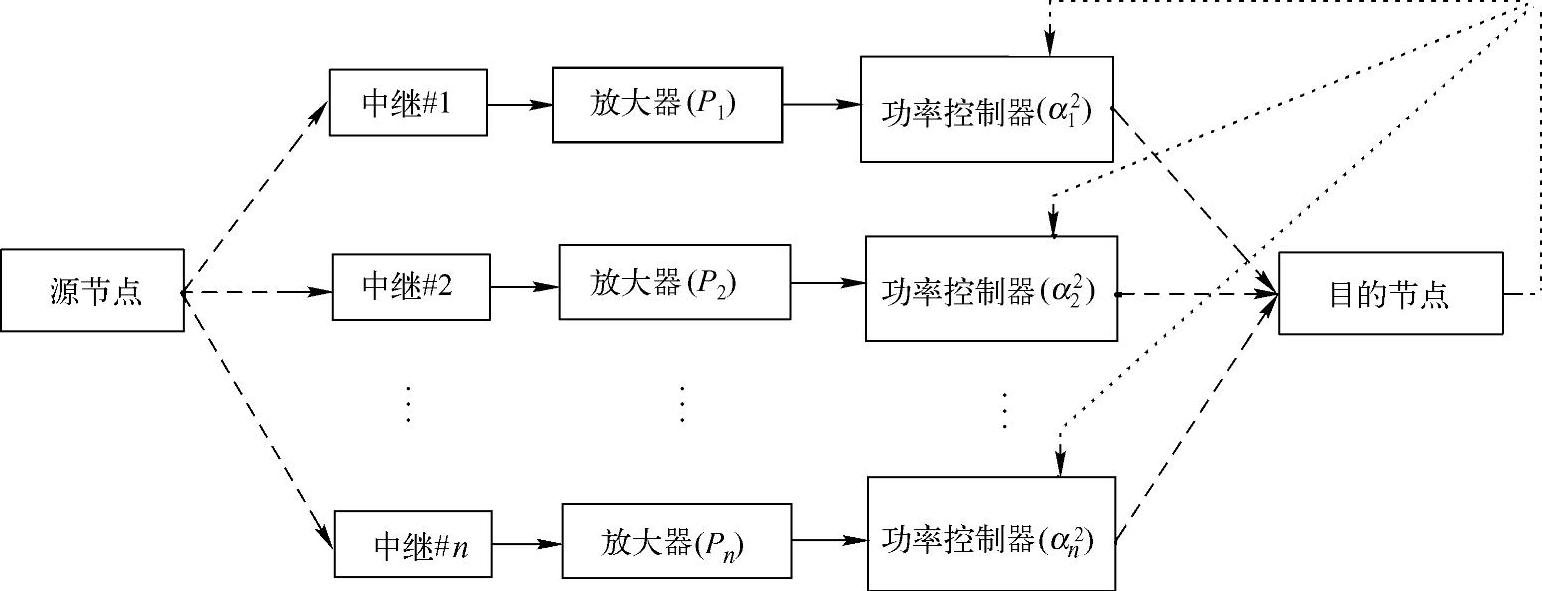
图3.23 单个中继功率受限的分布式波束赋型系统传输框图
3.3.4.4 仿真结果
本节中,我们仿真分析分别在全局总功率受限和单个中继功率受限两种条件下的波束赋型传输策略的性能。定义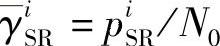 ,
, 。假设对于i=1,…,n,有
。假设对于i=1,…,n,有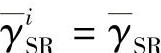 ,
,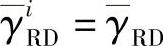 。图3.24~图3.26给出了不同的中继数和SNR下,中继总功率受限和单个中继功率受限两种功率约束的波束赋型方案的BER性能,横轴表示
。图3.24~图3.26给出了不同的中继数和SNR下,中继总功率受限和单个中继功率受限两种功率约束的波束赋型方案的BER性能,横轴表示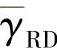 。从仿真曲线可见:基于单个中继功率受限的波束赋型方案相比于中继总功率受限下的方案存在1 dB的性能差异,单个中继功率受限是中继总功率受限的一种特例。两种方案都可以获得与中继数相同的分集度。
。从仿真曲线可见:基于单个中继功率受限的波束赋型方案相比于中继总功率受限下的方案存在1 dB的性能差异,单个中继功率受限是中继总功率受限的一种特例。两种方案都可以获得与中继数相同的分集度。
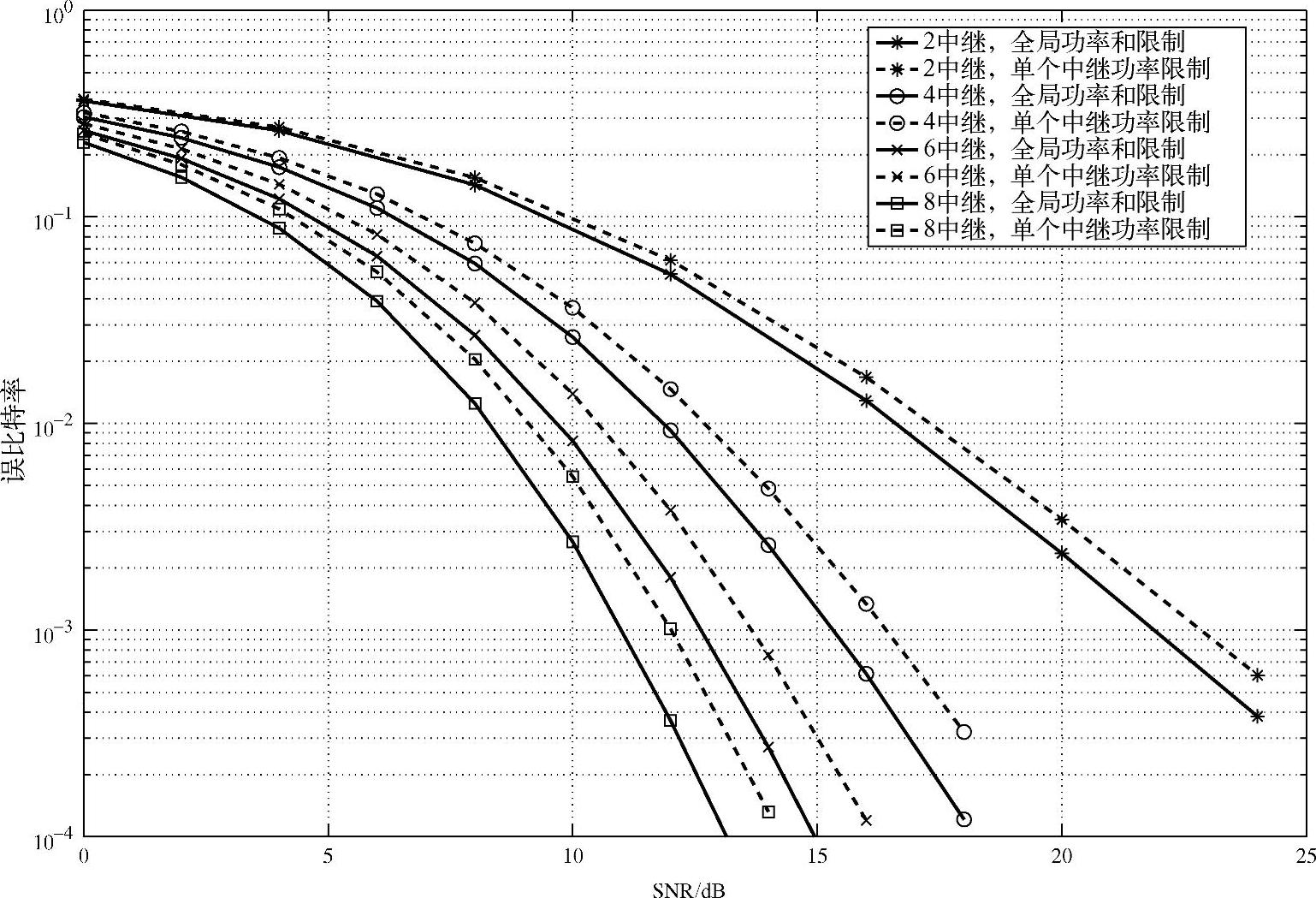
图3.24 不同中继数的BER性能比较,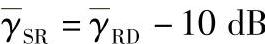
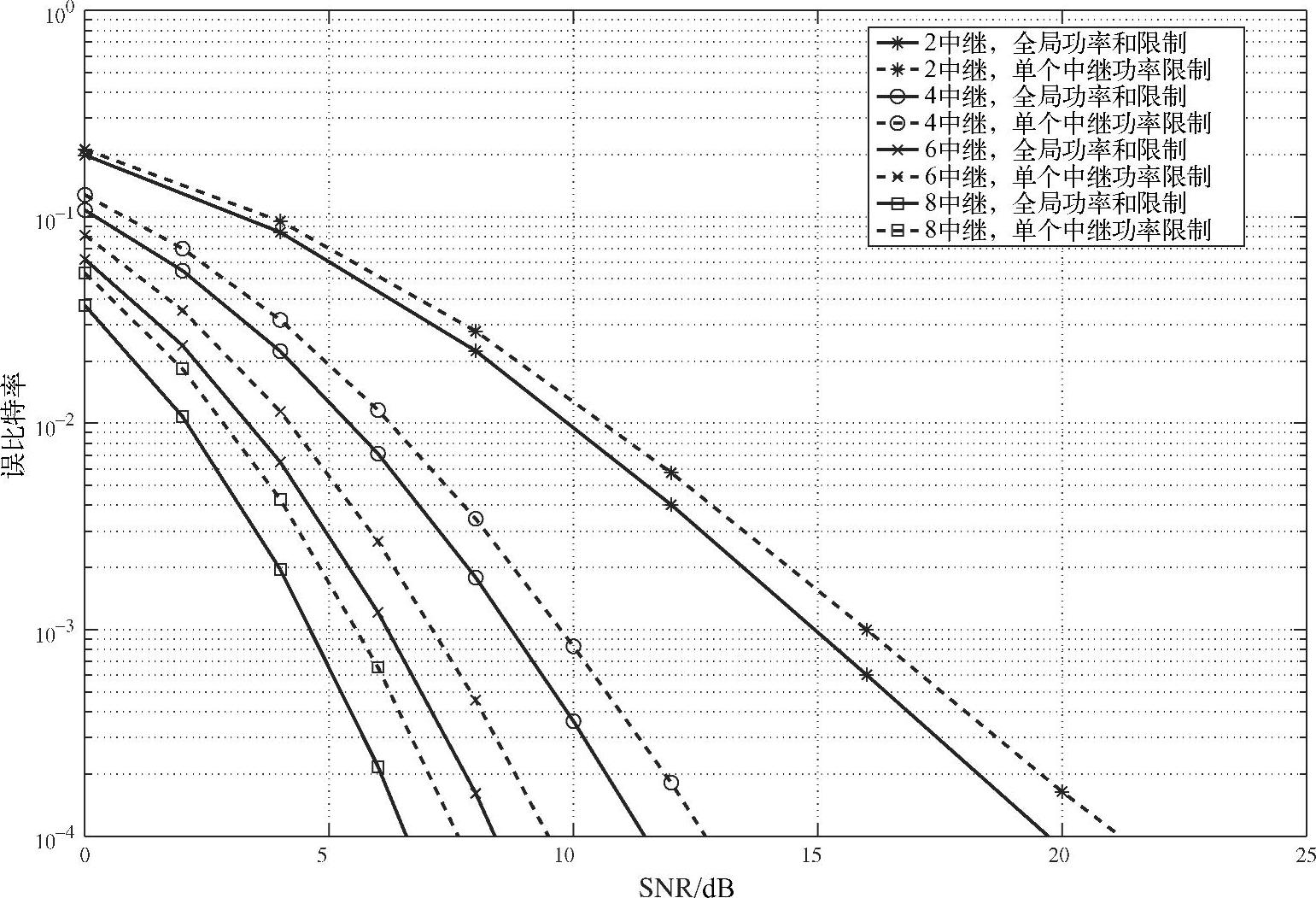
图3.25 不同中继数的BER性能比较,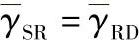
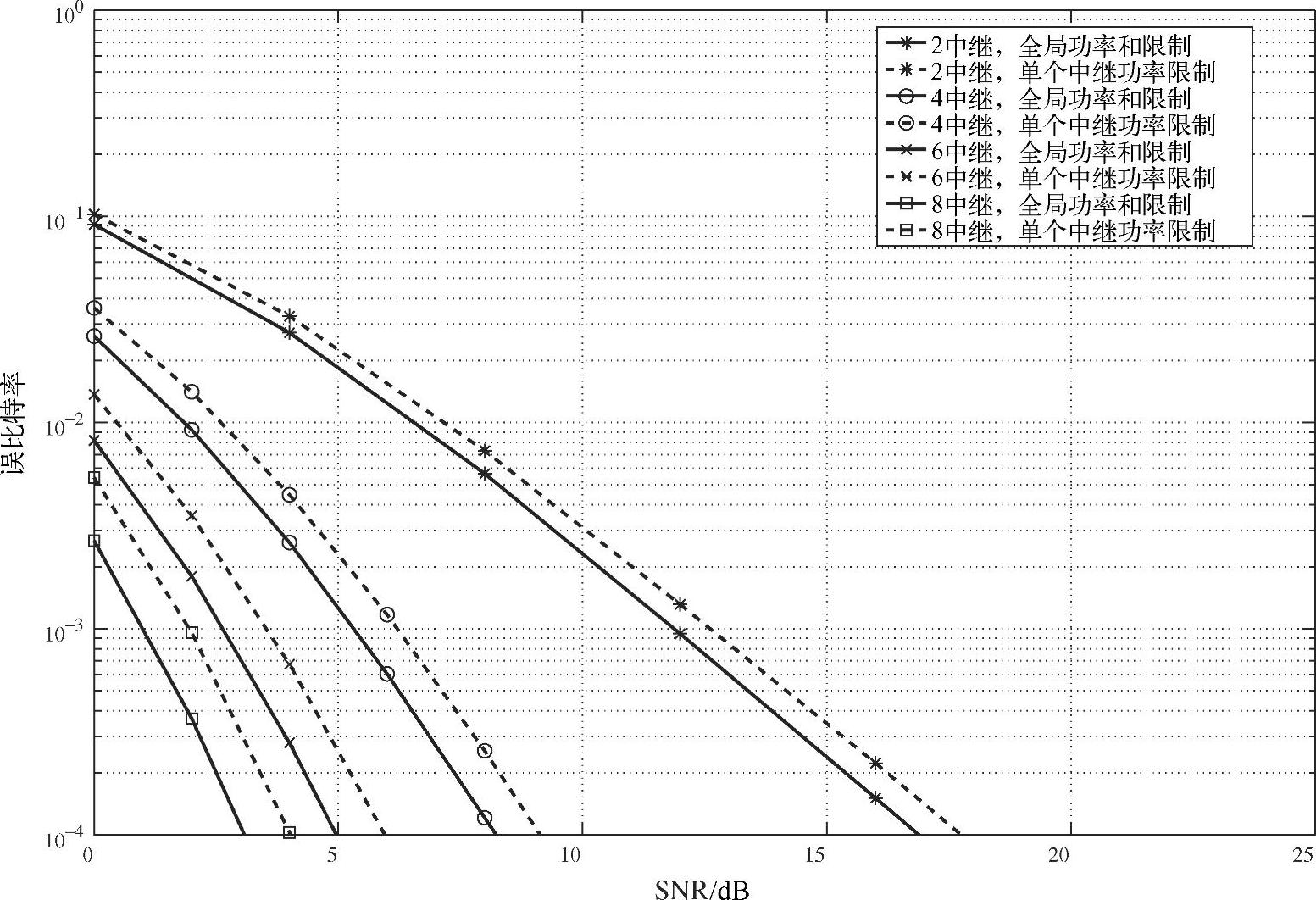
图3.26 不同中继数的BER性能比较,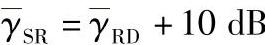
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




